▷ Fatorial de um número: o que é e como calculá-lo ✅

Esta página explica o que é o fatorial de um número e como ele é calculado. Além disso, são apresentados diversos exemplos e uma tabela com os valores dos fatoriais mais utilizados. Também ensina como calcular o fatorial de um número com a calculadora. E, finalmente, são ilustradas as aplicações e propriedades dos fatoriais.

Qual é o fatorial de um número?

Em matemática, o fatorial de um número é igual ao produto de todos os inteiros positivos de 1 até esse número. Além disso, o fatorial de um número é representado por um ponto de exclamação (!) após o número.

Por exemplo, para determinar o fatorial do número n , também chamado de fatorial n , deve-se multiplicar o número n por todos os inteiros que o precedem (começando por um):

$n! = 1 \cdot 2 \cdot 3 \cdots (n-2) \cdot (n-1) \cdot n$

Como calcular o fatorial de um número

Depois de vermos o significado do fatorial de um número, vamos ver com um exemplo como determinar qualquer fatorial:

Calcule o fatorial de 4:

Como vimos na sua definição matemática, o fatorial de um número equivale à multiplicação de todos os inteiros positivos menores ou iguais a ele. Portanto, para calcular o fatorial de 4, precisamos multiplicar os números 1, 2, 3 e 4:

$4! = 1 \cdot 2 \cdot 3 \cdot 4 =24$

O fatorial de 4, portanto, dá 24.

Exemplos de fatoriais de números

Para finalizar a compreensão da noção de fatorial de um número, deixamos um exemplo de cálculo de vários fatoriais de números diferentes:

Fatorial de 3:

$3! = 1 \cdot 2 \cdot 3 =6$

Fatorial de 5:

$5! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5=120$

Fatorial de 6:

$6! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6=720$

Fatorial de 1:

$1! = 1$

Logicamente, o fatorial do número 1 é igual a 1, pois basta multiplicar 1.

Fatorial de 0:

$0! = 1$

Sim, tudo bem, surpreendentemente, o fatorial de 0 não é igual a zero, mas sim a 1. Isso pode lhe parecer um pouco estranho, pois em teoria você tem que multiplicar 0 por 1. Porém, é adotado por convenção que 0! =1 porque a propriedade do produto está vazia . Deixamos este link caso você queira saber mais, embora não seja muito relevante que você saiba o motivo, o importante é que você lembre que o fatorial de 0 é igual a 1 .

Lista de resultados para fatoriais de números

Abaixo resumimos os fatoriais dos números mais usados em uma tabela, para que você não precise calculá-los manualmente.

O número	Fatorial do número
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5.040
8	40.320
9	362.880
dez	3.628.800
onze	39.916.800
12	479.001.600
13	6.227.020.800
14	87 178 291 200
quinze	1.307.674.368.000
16	20.922.789.888.000
17	355.687.428.096.000
18	6.402.373.705.728.000
19	121.645.100.408.832.000
vinte	2.432.902.008 176.640.000
cinquenta	3.041.409.320 · ^10,64
100	9.332 621.544 · ^10.157
1.000	4.023.872.601 · ^10.2567
10.000	2.846.259.681 · ^10.35.659
100.000	2 824 229 408 · 10 ^{45 6573}
1.000.000	8.263.931.688 · 10 ^5.565.708

Fatorial de um número com a calculadora

Como você pode ver nos exemplos anteriores, os resultados dos fatoriais de dois números consecutivos aumentam exponencialmente, por isso é bastante difícil conhecer o fatorial de números grandes. Então mostraremos como encontrar o fatorial de um número com a calculadora.

As calculadoras científicas possuem uma chave com o símbolo x! ou não! que é usado para calcular o fatorial de um número inteiro. Então, para determinar quanto vale um fatorial, você deve realizar a seguinte sequência na calculadora:

$n! \quad \color{red} \bm{\longrightarrow} \quad \color{black} n\rightarrow \boxed{x!} \rightarrow \boxed{=}$

Normalmente, as calculadoras CASIO possuem a chave fatorial x! ou não! acima do botão x ^-1 .

Como exemplo, resolveremos um fatorial com a calculadora para que você verifique se sabe como fazê-lo. Por exemplo, faremos o fatorial de 9:

$9! \quad \color{red} \bm{\longrightarrow} \quad \color{black} 9\rightarrow \boxed{x!} \rightarrow \boxed{=} \rightarrow 362880$

Para encontrar o fatorial de 9 você deve primeiro inserir o número 9 e depois pressionar a tecla

$\boxed{x!}$

e por fim, pressione o botão igual. Neste caso, a calculadora deverá nos mostrar o resultado de 362.880.

Aplicações do número fatorial

A função fatorial de um número pode parecer uma operação muito simples e absurda, mas em álgebra avançada ela é bastante utilizada. Veremos então os principais usos do fatorial.

Em primeiro lugar, o fatorial é uma operação essencial para o cálculo de um número combinatório , uma operação mais que particular. Se você não sabe o que é o número combinatório, pode ver em que consiste e como é calculado neste link, onde encontrará exemplos, exercícios resolvidos e quais são suas propriedades. Além disso, você poderá ver para que ele é usado, pois possui muitas aplicações no mundo real.

O fatorial também é usado em matemática para determinar o polinômio de Taylor de uma função.

Da mesma forma, o fatorial é utilizado para resolver certos problemas combinatórios, em particular para calcular combinações e permutações. Nesse sentido, os fatoriais também são frequentemente usados para calcular probabilidades por meio de combinatória.

Uma permutação de n elementos corresponde a cada um dos diferentes arranjos que podem ser feitos com estes elementos. Portanto, para calcular uma permutação, utiliza-se o fatorial. Por exemplo, se em um problema você quiser encontrar o número de possibilidades em que 7 objetos podem ser organizados, deverá calcular o fatorial de 7.

Agora vamos ver um exercício resolvido:

Temos 5 pares de sapatos diferentes, de quantas maneiras podemos organizá-los?

Neste exercício temos que descobrir todas as formas possíveis de combinar estes 5 pares de sapatos tendo em conta a ordem em que os colocamos. Então para resolver o problema basta calcular o fatorial de 5:

$5! = 1\cdot 2 \cdot 3\cdot 4\cdot 5 =120$

Resumindo, os 5 pares de sapatos podem ser colocados de 120 maneiras diferentes.

Propriedades do número fatorial

O número fatorial possui as seguintes características:

Sendo dois inteiros positivos n e m tais que n é maior que m , então, obviamente, o valor do fatorial de n é maior que o valor do fatorial de m .

$n>m \quad \longrightarrow \quad n! > m!” title=”Rendered by QuickLaTeX.com” height=”15″ width=”183″ style=”vertical-align: -2px;”> <ul style=$

O fatorial de um número pode ser decomposto fatorialmente de modo que um dos fatores seja o fatorial de um número menor.

$n>m \quad \longrightarrow \quad n!= n\cdot (n-1) \cdots (m+1)\cdot m!” title=”Rendered by QuickLaTeX.com” height=”19″ width=”361″ style=”vertical-align: -5px;”> Por exemplo, 6 é maior que 4, então a expressão para o fatorial de 6 pode ser simplificada da seguinte forma: <p class=$ $6! = 6 \cdot 5 \cdot 4!$

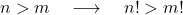
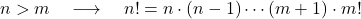
A seguinte expressão algébrica é válida para o fatorial de qualquer número, exceto o fatorial de 1:

$\displaystyle n!< \left( \frac{n+1}{2} \right)^n$

Fatorial de um número negativo ou decimal

Acabamos de ver como determinar o valor do fatorial de um número inteiro positivo, mas… podemos calcular o fatorial de um número negativo ou de um número decimal? A resposta é sim, mas é necessário conhecimento avançado de matemática.

O fatorial de um número negativo e de um número decimal é calculado usando uma função especial chamada “função gama” de Euler, que é definida pela seguinte integral:

$\displaystyle \Gamma(z)=\int_0^\infty t^{z-1} e^{-t}\, \mathrm{d}t$

Assim, qualquer tipo de fatorial pode ser resolvido com a função Gamma porque a seguinte equação é sempre verdadeira:

$n! = \Gamma(n+1)$

Então, para encontrar o fatorial de 0,5, por exemplo, devemos encontrar o valor de

$\Gamma(1,5)$

porque:

$0,5! = \Gamma(0,5+1) =\Gamma(1,5)$

E a solução da integral corresponderá ao fatorial de 0,5.

Obviamente resolver a integral da função Gama não é fácil e não iremos ensiná-la neste artigo, pois muitos conceitos matemáticos teriam que ser explicados previamente. Mas queríamos que você soubesse que existe a possibilidade de calcular o fatorial de um número negativo ou de um número decimal.

Na verdade, como exemplo, calculamos alguns valores fatoriais e decimais negativos:

$\underline{\bm{n}}$	$\underline{\bm{n!}}$
$\displaystyle \left(\frac{1}{2}\right)!$	$\displaystyle \frac{1}{2}\sqrt{\pi}$
$\displaystyle \left(-\frac{1}{2}\right)!$	$\displaystyle \sqrt{\pi}$
$\displaystyle \left(\frac{3}{2}\right)!$	$\displaystyle \frac{3}{4}\sqrt{\pi}$
$\displaystyle \left(\frac{5}{2}\right)!$	$\displaystyle \frac{15}{8}\sqrt{\pi}$