Nesta página você descobrirá o que são funções exponenciais e também como representar uma função exponencial em um gráfico. Além disso, você verá todas as suas características e diversos exemplos para entendê-lo totalmente. Por fim, você poderá praticar exercícios e problemas resolvidos passo a passo em funções exponenciais.
O que é uma função exponencial?
A definição de uma função exponencial é a seguinte:
Em matemática, funções exponenciais são funções que possuem a variável independente x no expoente de uma potência. Em outras palavras, eles são os seguintes:
![]()
Ouro
![]()
é um número real positivo e diferente de 1.
Exemplos de funções exponenciais
As seguintes funções são exemplos de funções exponenciais:
![]()
![]()
![]()
![]()
Características das funções exponenciais
As funções exponenciais têm as seguintes propriedades:
- O domínio de uma função exponencial consiste em números reais, ou em outras palavras, existe uma função exponencial para qualquer valor de x .
![]()
- No entanto, a função aceita apenas valores positivos, portanto o contradomínio de uma função exponencial consiste em números reais positivos.
![]()
- Toda função exponencial é uma função contínua e injetiva.
- Se a função não for traduzida, qualquer função exponencial passa pelo ponto (0,1). Porque a função avaliada como zero sempre dá um.
![]()
- Da mesma forma, o valor de uma função exponencial em x=1 é igual à base.
![]()
- Se a base de poder
é maior que 1, a função exponencial está aumentando. Por outro lado, se o coeficiente

está no intervalo entre 0 e 1, a função exponencial está diminuindo.
- Em geral, o eixo x é uma assíntota horizontal de uma função exponencial.
- O inverso da função exponencial é a função logarítmica. Portanto, os gráficos de uma função exponencial e de uma função logarítmica são simétricos em relação à reta y=x se ambas tiverem a mesma base.
Como representar graficamente uma função exponencial
As funções exponenciais são muito simples de representar. Então, vamos ver como representar graficamente uma função exponencial em um gráfico usando um exemplo.
- Trace a seguinte função exponencial em um gráfico:
![]()
Nas funções exponenciais não há necessidade de calcular o domínio, pois sempre serão todos números reais:
![]()
Basta, portanto, elaborar a tabela de valores. Como esses tipos de funções mudam muito de um ponto para outro, calcularemos 5 pontos. Mas quanto mais pontos calcularmos, mais precisa será a representação da função.

Recomendamos o uso de uma calculadora para encontrar os pontos da tabela de valores, pois são complicados de calcular manualmente.
Agora representamos os pontos em um gráfico :

E finalmente, juntamos os pontos e estendemos a função:
Observe que a função à direita continua a crescer até o infinito.
Em contraste, a função à esquerda diminui, mas nunca chega a 0. Mesmo chegando muito perto dela, nunca a toca. Isso significa que a reta y=0 (o eixo x) é uma assíntota horizontal.
Exercícios resolvidos sobre funções exponenciais
Exercício 1
Faça um gráfico da seguinte função exponencial:
![]()
É uma função exponencial, portanto para representá-la é necessário criar uma tabela de valores dando valores à variável x:
![]()
![]()
![]()
![]()
![]()

Assim que tivermos a tabela de valores, plotamos os pontos obtidos no gráfico e plotamos a função:

Observe que a função à direita continua a crescer até o infinito. Por outro lado, à esquerda, a função diminui, mas nunca excede 1. Na verdade, a função tem uma assíntota horizontal à direita y=1.
Neste caso, a assíntota horizontal está em y=1 em vez do eixo OX porque uma translação vertical de uma unidade para cima foi feita em direção à função.
Exercício 2
Trace a seguinte função exponencial em um gráfico:
![]()
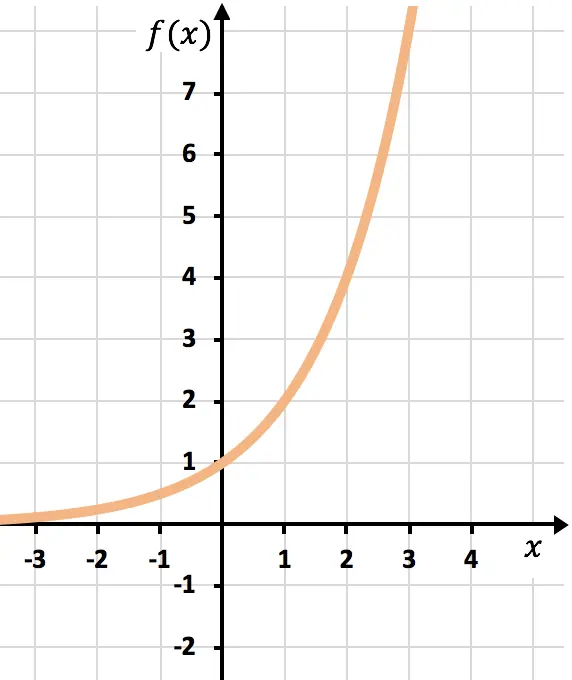
É uma função exponencial, portanto para representá-la graficamente é necessário construir uma tabela de valores dando valores à variável x:
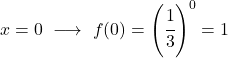
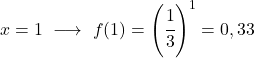
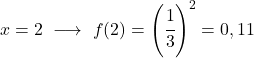
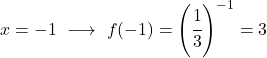
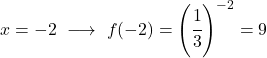
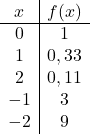
Assim que tivermos a tabela de valores, plotamos os pontos calculados no gráfico e desenhamos a função:

Observe que a função à esquerda continua a crescer até o infinito. Por outro lado, à direita, a função diminui, mas nunca excede 0. Na verdade, a função tem uma assíntota horizontal em y=0 (o eixo X).
Exercício 3
Trace a seguinte função exponencial em um gráfico:
![]()
É uma função exponencial, portanto para desenhá-la é necessário criar uma tabela de valores avaliando a função em vários pontos:
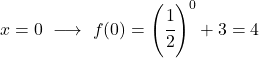
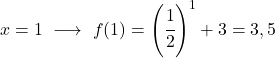
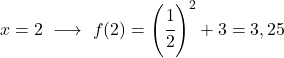
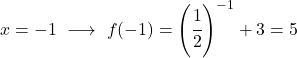
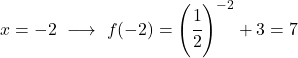

Por fim, representamos os pontos obtidos no gráfico e traçamos a função:

Observe que a função à esquerda cresce ilimitadamente até o infinito. Por outro lado, à direita, a função diminui mas nunca excede 3. Na verdade, a função tem uma assíntota horizontal em y=3.
Neste caso, a assíntota horizontal está em y=3 em vez do eixo X porque a função foi movida verticalmente três unidades para cima.
Exercício 4
Resolva o seguinte problema relacionado a funções exponenciais.
- Determine o valor de

de modo que a próxima função exponencial passe pelo ponto (2.8).
![]()
A função deve passar pelo ponto (2,8), então podemos substituir os valores de x e f(x) do ponto na função para encontrar o valor da constante k:
![]()
E agora resolvemos a equação resultante:
![]()
![]()
![]()
![]()
Exercício 5
Resolva o seguinte problema relacionado a funções exponenciais.
Uma população de cupins se reproduz de acordo com a seguinte função:
![]()
Ouro
![]()
é o número de cupins e
![]()
o tempo passou em meses.
Quantos cupins existirão após 1 ano?
Para calcular o número de cupins que haverá em um ano, basta substituir o tempo decorrido (1 ano) na função. Mas como a função t são os meses decorridos e não os anos, devemos colocar t =12 já que num ano há 12 meses:
![]()
![]()
![]()
Resolvemos com a calculadora:
![]()
Então, depois de um ano, haverá 1.594.323 cupins.