▷ Concavidade e convexidade de uma função (curvatura)

Aqui você aprenderá o que são concavidade e convexidade de uma função e como saber se uma função é côncava ou convexa. Além disso, você poderá praticar exercícios passo a passo sobre a curvatura de uma função.

Qual é a concavidade e a convexidade de uma função?

A concavidade e a convexidade de uma função referem-se à curvatura do gráfico de uma função. Uma função côncava é uma função cujo gráfico tem a forma de uma montanha, e uma função convexa é uma função cujo gráfico tem a forma de um vale.

No parágrafo anterior, as funções côncavas e convexas foram definidas informalmente para facilitar a compreensão, mas a definição matemática de função côncava e função convexa é a seguinte:

Função côncava: quando o segmento que une quaisquer dois pontos da função está abaixo da curva.
Função convexa: quando o segmento que une quaisquer dois pontos da função está acima da curva.

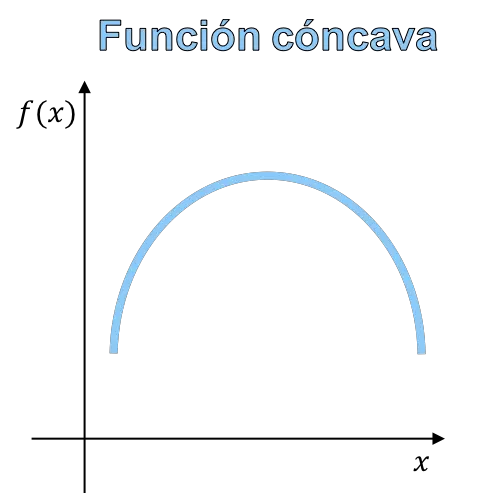
Em última análise, a diferença entre uma função côncava e uma função convexa está na forma da função e, portanto, você pode distinguir a concavidade da convexidade no gráfico da função.

No entanto, uma função não precisa necessariamente ser côncava ou convexa em todo o seu domínio, mas também pode ser côncava em um intervalo e convexa em outro intervalo.

Nota: A comunidade matemática ainda não concorda plenamente e, por isso, alguns professores dizem o contrário: chamam uma função côncava aquela que tem a forma de um

$\bm{\cup}$

, e uma função convexa que tem a forma de

$\bm{\cap}$

. De qualquer forma, o importante é saber qual é a função, seja qual for o nome.

Como estudar a curvatura de uma função

Estudar a curvatura de uma função envolve encontrar a concavidade e a convexidade da função, ou seja, conhecer os intervalos em que a função é côncava e os intervalos em que a função é convexa.

Portanto, para estudar a curvatura de uma função, devem ser executados os seguintes passos:

Encontre os pontos que não pertencem ao domínio da função.
Calcule a primeira derivada e a segunda derivada da função.
Encontre as raízes da segunda derivada , ou seja, calcule os pontos que cancelam a segunda derivada resolvendo
$f''(x)=0$

.
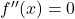
Faça intervalos com as raízes da derivada e os pontos que não pertencem ao domínio da função.
Calcule o valor da segunda derivada em um ponto de cada intervalo.
Assim, o sinal da segunda derivada determina a concavidade ou convexidade da função neste intervalo:
- Se a segunda derivada da função for positiva, a função é convexa neste intervalo.
- Se a segunda derivada da função for negativa, a função é côncava neste intervalo.

Exemplo de como encontrar a curvatura de uma função

A seguir, resolveremos um exemplo passo a passo para que você possa ver como são calculados os intervalos de concavidade e convexidade de uma função.

Estude a concavidade e a convexidade da seguinte função:

$f(x)=x^3-3x$

A primeira coisa a fazer é calcular o domínio de definição da função. Neste caso, temos uma função polinomial, então o domínio da função consiste em números reais:

$\text{Dom } f= \mathbb{R}$

Depois de calcularmos o domínio da função, precisamos investigar em que pontos a segunda derivada da função desaparece.

Portanto, calculamos a primeira derivada da função:

$f(x)=x^3-3x \ \longrightarrow \ f'(x)= 3x^2-3$

Encontramos então a segunda derivada da função:

$f'(x)=3x^2-3 \ \longrightarrow \ f''(x)= 6x$

E agora definimos a segunda derivada igual a 0 e resolvemos a equação:

$f''(x)=0$

$6x=0$

$x=\cfrac{0}{6}$

$x=0$

Depois de calcularmos o domínio da função e

$f''(x)=0$

, representamos todos os pontos críticos encontrados na linha. Neste caso não encontramos nenhum ponto crítico no cálculo do domínio de definição da função, mas obtivemos um ponto que anula a segunda derivada da função:

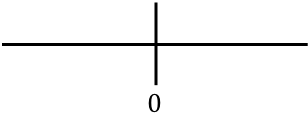
E agora avaliamos o sinal da segunda derivada em cada intervalo, para saber se a função é côncava ou convexa. Portanto, pegamos um ponto em cada intervalo (nunca os pontos críticos) e observamos qual sinal a segunda derivada tem neste ponto:

$f''(x)=6x$

$f''(-1) = 6\cdot (-1)=-6 \ \rightarrow \ \bm{-}$

$f''(1) = 6\cdot 1=+6 \ \rightarrow \ \bm{+}$

Finalmente, deduzimos os intervalos de concavidade e convexidade da função. Se a segunda derivada for positiva, significa que a função é convexa.

$(\bm{\cup})$

, e se a segunda derivada for negativa isso significa que a função é côncava

$(\bm{\cap})$

. Assim, os intervalos de concavidade e convexidade da função são:

Convexo

$(\bm{\cup})$

$\bm{(0,+\infty)}$

Côncavo

$(\bm{\cap})$

$\bm{(-\infty,0)}$

Exercícios resolvidos sobre concavidade e convexidade de uma função

Exercício 1

Calcule os intervalos de concavidade e convexidade da seguinte função polinomial:

$f(x) = x^3-3x^2-2x$

Veja a solução

A função no exercício é um polinômio, então o domínio da função consiste em números reais:

$\text{Dom } f= \mathbb{R}$

Depois de determinar o domínio da função, diferenciamo-lo:

$f(x)=x^3-3x^2-2x \ \longrightarrow \ f'(x)= 3x^2-6x-2$

Encontramos então a segunda derivada da função:

$f'(x)= 3x^2-6x-2 \ \longrightarrow \ f''(x)= 6x-6$

E agora definimos a segunda derivada igual a 0 e resolvemos a equação:

$f''(x)= 0$

$6x-6= 0$

$6x= 6$

$x= \cfrac{6}{6}$

$x=1$

Depois de calcularmos o domínio da função e resolvermos

$f''(x)=0$

, representamos todos os pontos singulares encontrados na reta numérica:

E agora vamos pegar um ponto pertencente a cada intervalo e ver qual sinal tem a segunda derivada neste ponto:

$f''(0)= 6\cdot 0-6 = -6 \ \rightarrow \ \bm{-}$

$f''(2)= 6\cdot 2-6 = 12-6=+6 \ \rightarrow \ \bm{+}$

Quando a segunda derivada é maior que zero, significa que a função é convexa.

$(\bm{\cup})$

, mas quando a segunda derivada é negativa isso implica que a função é côncava

$(\bm{\cap})$

. Portanto, os intervalos de concavidade e convexidade são:

Convexo

$(\bm{\cup})$

$\bm{(1,+\infty)}$

Côncavo

$(\bm{\cap})$

$\bm{(-\infty,1)}$

Exercício 2

Estude a curvatura da seguinte função racional:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Veja a solução

Primeiro precisamos calcular o domínio da função. Como se trata de uma função racional, igualamos o denominador a zero para ver quais números não pertencem ao domínio da função:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

Isso significa que quando x for -2 ou +2, o denominador será 0. E portanto, a função não existirá. O domínio da função é, portanto, composto por todos os números, exceto x=-2 e x=+2.

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

Segundo, calculamos a primeira derivada da função:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

E então resolvemos a segunda derivada:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

Todos os termos são multiplicados por

$(x^2-4)$

. Podemos, portanto, simplificar a fração:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Agora vamos calcular as raízes da segunda derivada da função:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

O termo

$\left(x^2-4\right)^3$

Isso envolve dividir todo o lado esquerdo, para que possamos multiplicá-lo por todo o lado direito:

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

Extraímos o fator comum:

$x(8x^2+96)=0$

Para que a multiplicação seja igual a 0, um dos dois elementos da multiplicação deve ser zero. Portanto, definimos cada fator igual a 0:

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

Não há solução, pois não existe raiz negativa de um número real.

Representamos agora na reta todos os pontos críticos obtidos, ou seja, os pontos que não pertencem ao domínio (x=-2 e x=+2) e aqueles que cancelam a segunda derivada (x=0):

E avaliamos o sinal da segunda derivada em cada intervalo, para saber se a função é côncava ou convexa. Então pegamos um ponto em cada intervalo e observamos qual sinal tem a segunda derivada nesse ponto:

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

Se a segunda derivada for positiva, significa que a função é convexa.

$(\bm{\cup})$

, e se a segunda derivada for negativa isso significa que a função é côncava

$(\bm{\cap})$

. Os intervalos de concavidade e convexidade são, portanto:

Convexo

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

Côncavo

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

Exercício 3

Uma função

$f(x)$

tem um extremo relativo em

$x=3$

. E mais, a função é convexa

$(\cup )$

neste mesmo ponto. Determine se o extremo relativo é mínimo ou máximo.

➤ Veja: definição de máximos e mínimos de uma função

Veja a solução

Deixe a função convexa

$(\cup)$

$x=3$

significa que a segunda derivada neste ponto é positiva, ou seja

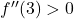$f''(3)>0″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”74″ style=”vertical-align: -5px;”></p> <p> .</p> <p class=$ Portanto, o extremo relativo de

$\bm{x=3}$

Este é o mínimo , pois

$f''(3)$

É positivo.

Qual é a concavidade e a convexidade de uma função?

Como estudar a curvatura de uma função

Exemplo de como encontrar a curvatura de uma função

Exercícios resolvidos sobre concavidade e convexidade de uma função

Exercício 1

Exercício 2

Exercício 3

Deixe um comentário Cancelar resposta