Função cosseno hiperbólico

Aqui você encontrará tudo sobre a função cosseno hiperbólico: qual a sua fórmula, sua representação gráfica, suas características, as relações matemáticas com outras funções, etc.

Fórmula hiperbólica do cosseno

A função cosseno hiperbólica é uma das principais funções hiperbólicas e é representada pelo símbolo cosh(x) . O cosseno hiperbólico é igual à soma de e ^x mais e ^-x dividido por 2.

Portanto, a fórmula do cosseno hiperbólico é:

$\displaystyle\text{cosh}(x)=\cfrac{e^{x}+e^{-x}}{2}$

Assim, o cosseno hiperbólico está matematicamente relacionado à função exponencial. No link a seguir você pode ver as propriedades deste tipo de função:

➤ Veja: propriedades da função exponencial

Representação gráfica do cosseno hiperbólico

A representação gráfica da função cosseno hiperbólico tem a forma de uma função quadrática (ou parábola):

➤ Veja: Representação gráfica de uma função quadrática .

Neste gráfico, podemos ver claramente que o cosseno hiperbólico é uma função par, porque é simétrico em relação ao eixo y.

Por outro lado, o gráfico do cosseno hiperbólico é muito diferente daquele do cosseno (função trigonométrica), que é uma função periódica. Você pode ver a representação gráfica do cosseno e todas as diferenças com o cosseno hiperbólico no seguinte link:

➤ Veja: representação gráfica da função cosseno

Características do cosseno hiperbólico

O cosseno hiperbólico respeita as seguintes propriedades:

O domínio da função cosseno hiperbólico são todos os números reais:

$\text{Dom } f = \mathbb{R}$

Em vez disso, o intervalo (ou intervalo) da função cosseno hiperbólica é 1 e todos os números maiores que 1:

$\text{Im } f= [1,+\infty)$

O cosseno hiperbólico é uma função contínua e par.

$\displaystyle \text{cosh}(-x)=\text{cosh}(x)$

A função intercepta o eixo Y no ponto x=0.

$(0,1)$

Por outro lado, a função não tem ponto de intersecção com o eixo X.

Os dois limites ao infinito (positivo e negativo) da função cosseno hiperbólica dão mais infinito.

$\displaystyle\lim_{x\to+\infty}\text{cosh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{cosh}(x)=+\infty$

O cosseno hiperbólico diminui até x = 0 e a partir desse ponto aumenta indefinidamente, então a função tem mínimo em x = 0.

$(0,1)$

A função é convexa em todo o seu domínio, portanto não possui ponto de inflexão.

A derivada da função cosseno hiperbólico é o seno hiperbólico:

$f(x)=\text{cosh}(x) \ \longrightarrow \ f'(x)=\text{senh}(x)$

A integral da função cosseno hiperbólico é o seno hiperbólico:

$\displaystyle \int \text{cosh}(x) \ dx= \text{senh}(x) + C$

O polinômio de Taylor (ou série de Maclaurin) da função cosseno hiperbólica é o seguinte:

$\displaystyle\text{cosh}(x)=1+\cfrac{x^2}{2!}+\cfrac{x^4}{4!}+\cfrac{x^6}{6!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n}}{(2n)!}$

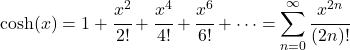
A transformada de Laplace da função cosseno hiperbólica é a seguinte:

$\mathcal{L}\bigl[\text{cosh}(at)\bigr]=\cfrac{s}{s^2-a^2}$

Relações matemáticas do cosseno hiperbólico

A seguir, veremos como o cosseno hiperbólico pode ser calculado a partir de outras funções hiperbólicas, uma vez que todas estão matematicamente relacionadas.

A equação fundamental relaciona o cosseno hiperbólico ao seno hiperbólico:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

➤ Veja: seno hiperbólico

As três principais funções hiperbólicas (seno, cosseno e tangente hiperbólicos) podem ser relacionadas pela seguinte equação:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

Por outro lado, o cosseno hiperbólico da adição (ou subtração) de dois números diferentes pode ser determinado pelas seguintes fórmulas:

$\text{cosh}(x+y)=\text{cosh}(x)\text{cosh}(y)+\text{senh}(y)\text{senh}(x)$

$\text{cosh}(x-y)=\text{cosh}(x)\text{cosh}(y)-\text{senh}(y)\text{senh}(x)$

O cosseno hiperbólico de duas vezes um número é igual à soma dos quadrados do cosseno hiperbólico e do seno hiperbólico deste número:

$\text{cosh}(2x)=\text{cosh}^2(x)+\text{senh}^2(x)$

A adição ou subtração de dois cossenos hiperbólicos pode ser calculada aplicando as seguintes fórmulas:

$\displaystyle\text{cosh}(x)+\text{cosh}(y)=2\text{cosh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{cosh}(x)-\text{cosh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{senh}\left(\frac{x-y}{2}\right)$

Finalmente, o quadrado do cosseno hiperbólico pode ser calculado com a seguinte fórmula:

$\text{cosh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)+1\Bigr)$

Função cosseno hiperbólica

Fórmula hiperbólica do cosseno

Representação gráfica do cosseno hiperbólico

Características do cosseno hiperbólico

Relações matemáticas do cosseno hiperbólico

Deixe um comentário Cancelar resposta