Frações algébricas: simplificação, operações, exercícios resolvidos, etc. -

Nesta página explicamos o que são frações algébricas, quando são equivalentes, como simplificá-las e como realizar operações com frações algébricas (adição, subtração, multiplicação e divisão). Além disso, você poderá ver passo a passo exercícios resolvidos para frações algébricas. Resumindo, aqui você encontrará tudo sobre frações algébricas.

O que são frações algébricas?

Em matemática, uma fração algébrica é uma fração que possui um polinômio no numerador e outro polinômio no denominador.

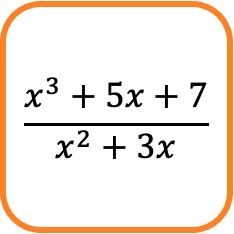
Por exemplo, a expressão fracionária acima consiste em uma fração algébrica porque seu numerador e denominador são compostos de polinômios.

Equivalente de fração algébrica

Depois de sabermos a definição de frações algébricas, vamos ver quando duas dessas frações são iguais.

Matematicamente, duas frações algébricas são equivalentes se a seguinte condição for atendida:

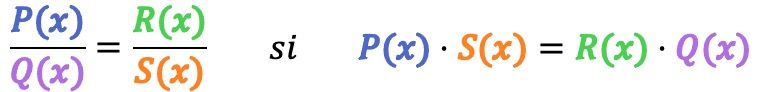
Como exemplo, verificaremos se as 2 frações algébricas a seguir são equivalentes:

$\cfrac{x+3}{x^2+5x+6} \qquad \cfrac{1}{x+2}$

Para determinar se as frações são algebricamente iguais, multiplicamos seus termos transversalmente:

$(x+3)\cdot (x+2) = (x^2+5x+6)\cdot 1$

Agora vamos calcular as multiplicações de polinômios:

$x^2+2x+3x+6 = x^2+5x+6$

$x^2+5x+6 = x^2+5x+6$

Obtivemos a mesma expressão em ambos os lados da equação, portanto são efetivamente duas frações algébricas equivalentes.

Simplifique frações algébricas

Para simplificar uma fração algébrica, primeiro você deve fatorar os polinômios no numerador e no denominador e, em seguida, eliminar os fatores que eles têm em comum.

Obviamente, para simplificar frações algébricas, é fundamental que você saiba o que é fatoração polinomial e como ela é feita. Se você ainda não sabe como os polinômios são fatorados ou não se lembra completamente, recomendo ir à página vinculada antes de continuar, caso contrário você mal entenderá o procedimento. Explica passo a passo como fatorar polinômios e, além disso, você poderá ver diversos exemplos e praticar com exercícios resolvidos.

Agora vamos ver como uma fração algébrica é simplificada aplicando o método de fatoração de polinômios usando um exemplo:

Simplifique a seguinte fração algébrica:

$\cfrac{x^3+2x^2-x-2}{x^2-2x+1}$

Primeiro, fatoramos os polinômios do numerador e denominador da fração:

$\cfrac{(x-1)(x+1)(x+2)}{(x-1)(x-1)}$

⬆(Se você não sabe como os polinômios foram fatorados, dê uma olhada no link acima)⬆

E uma vez fatorados os polinômios, eliminamos os fatores comuns entre o numerador e o denominador, ou seja, removemos todos os termos que se repetem:

$\cfrac{\cancel{(x-1)}(x+1)(x+2)}{\cancel{(x-1)}(x-1)}$

A fração algébrica simplificada, portanto, fica assim:

$\cfrac{(x+1)(x+2)}{x-1}$

Neste problema, os polinômios da fração algébrica foram fatorados encontrando suas raízes; entretanto, às vezes um polinômio pode ser fatorado diretamente usando o fator comum (método muito mais rápido). Neste link você verá o que significa extrair um fator comum de um polinômio e descobrirá como simplificar uma fração algébrica usando um fator comum.

Operações com frações algébricas

Como qualquer tipo de fração, as operações também podem ser realizadas com frações algébricas. Especificamente, as frações algébricas podem ser adicionadas, subtraídas, multiplicadas e divididas. Abaixo explicamos passo a passo com exemplos como cada tipo de operação é calculado.

Adição e subtração de frações algébricas

O procedimento de adição e subtração de frações algébricas é praticamente idêntico, por isso iremos analisá-los em conjunto. Primeiro veremos um exemplo de adição de duas frações algébricas, e a seguir estudaremos a diferença entre o método de subtração de frações algébricas.

Adicionando frações algébricas

A adição de frações algébricas é feita da mesma maneira que com frações normais: primeiro reduza as frações a um denominador comum e depois adicione os numeradores.

Vamos ver como as frações algébricas são adicionadas usando um exemplo:

$\cfrac{x}{x^2+2x+1} + \cfrac{3x}{x^2+x}$

Primeiro fatoramos os denominadores das frações:

$\cfrac{x}{(x+1)(x+1)} + \cfrac{3x}{x(x+1)}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

Agora precisamos encontrar o lcm (mínimo múltiplo comum) dos denominadores para reduzir as frações a um denominador comum.

Dica: o lcm dos denominadores é sempre formado a partir do produto dos fatores que eles têm em comum elevado ao maior expoente multiplicado pelos fatores não comuns .

Por exemplo, no nosso caso

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

O divisor comum entre os denominadores elevados ao maior expoente é

$(x+1)^2.$

E o fator não comum entre os denominadores é

$x.$

Portanto, o lcm dos denominadores neste caso é:

$(x+1)^2 \cdot x$

O lcm dos denominadores é, portanto,

$(x+1)^2 \cdot x,$

este será, portanto, o novo denominador das 2 frações.

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{}{x(x+1)^2} + \cfrac{}{x(x+1)^2}$

Depois de encontrar o denominador comum, devemos modificar os numeradores. Para fazer isso, seguimos o mesmo processo da adição de frações normais: para cada fração dividimos o lcm

$\bigl( \ x(x+1)^2 \ \bigr)$

entre o denominador original e multiplique o resultado pelo numerador:

$\cfrac{x(x+1)^2}{(x+1)^2} = \cfrac{x\cancel{(x+1)^2}}{\cancel{(x+1)^2}} = \color{red}\bm{x}$

$\cfrac{x(x+1)^2}{x(x+1)}= \cfrac{\cancel{x}(x+1)^\cancel{2}}{\cancel{x}\cancel{(x+1)}}=\color{blue} \bm{x+1}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{x \cdot \color{red}\bm{x} \color{black} }{x(x+1)^2} + \cfrac{3x \cdot \color{blue} \bm{(x+1)} \color{black}}{x(x+1)^2}$

Então agora podemos juntar as duas frações porque elas têm o mesmo denominador:

$\cfrac{x^2+3x(x+1)}{x(x+1)^2}$

Finalmente, operamos no numerador. Primeiro fazemos o produto do monômio e do polinômio:

$\cfrac{x^2 +3x\cdot x+ 3x\cdot 1 }{x(x+1)^2}$

$\cfrac{x^2 +3x^2 + 3x }{x(x+1)^2}$

A seguir, adicionamos os termos semelhantes ao numerador:

$\cfrac{4x^2 + 3x }{x(x+1)^2}$

Normalmente já estaríamos lá, mas se olharmos este problema de perto, podemos simplificar ainda mais a fração algébrica removendo um fator comum do numerador. Ainda:

$\cfrac{x(4x + 3)}{x(x+1)^2}$

$\cfrac{\cancel{x}(4x + 3)}{\cancel{x}(x+1)^2}$

$\cfrac{4x + 3}{(x+1)^2}$

E assim já completamos a soma das duas frações algébricas.

Subtração de frações algébricas

Para subtrair frações algébricas, devemos seguir um procedimento semelhante à adição de frações algébricas: primeiro reduza as frações a um denominador comum e depois subtraia os numeradores.

Vamos ver como as frações algébricas são subtraídas com um exemplo:

$\cfrac{2x}{x^2-x-6} - \cfrac{4x-3}{(x+2)^2}$

Primeiro, precisamos fatorar os denominadores das duas frações:

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2}$

Tal como acontece com a subtração de frações normais, devemos agora calcular o lcm (mínimo múltiplo comum) dos denominadores para reduzir as frações a um denominador comum. Neste caso, o lcm dos denominadores é

$(x+2)^2(x-3) ,$

este será, portanto, o novo denominador das 2 frações.

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{}{(x+2)^2(x-3)} + \cfrac{}{(x+2)^2(x-3)}$

Agora aplicamos o mesmo processo de subtração de frações normais: para cada fração dividimos o lcm

$\bigl( \ x(x+1)^2 \ \bigr)$

entre o denominador original e multiplique o resultado pelo numerador:

$\cfrac{(x+2)^2(x-3)}{(x+2)(x-3)} = \cfrac{(x+2)^{\cancel{2}}\cancel{(x-3)}}{\canel{(x+2)}\cancel{(x-3)}} = \color{red}\bm{x+2}$

$\cfrac{(x+2)^2(x-3)}{(x+2)^2}= \cfrac{\cancel{(x+2)^2}(x-3)}{\cancel{(x+2)^2}}=\color{blue} \bm{x-3}$

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{2x\cdot \color{red}\bm{(x+2)} \color{black}}{(x+2)^2(x-3)} + \cfrac{(4x-3)\cdot \color{blue} \bm{(x-3)} \color{black}}{(x+2)^2(x-3)}$

Agora juntamos as duas frações algébricas, pois elas têm o mesmo denominador:

$\cfrac{2x(x+2)-(4x-3)(x-3)}{(x+2)^2(x-3)}$

E operamos no numerador. Primeiro resolvemos as multiplicações polinomiais:

$\cfrac{2x^2+4x-\bigl[4x^2-12x-3x+9\bigr]}{(x+2)^2(x-3)}$

Um erro muito comum ao subtrair frações algébricas é esquecer de colocar parênteses após realizar esta multiplicação. Isto seria um erro, pois o sinal negativo afeta todos os elementos resultantes do produto, e não apenas o primeiro termo.

Realizamos as operações entre parênteses:

$\cfrac{2x^2+4x-\bigl[4x^2-15x+9\bigr]}{(x+2)^2(x-3)}$

Assim, graças ao sinal negativo, mudamos o sinal de todos os termos entre parênteses:

$\cfrac{2x^2+4x-4x^2+15x-9}{(x+2)^2(x-3)}$

E, por fim, agrupamos monômios semelhantes:

$\cfrac{-2x^2+19x-9}{(x+2)^2(x-3)}$

Multiplicação de frações algébricas

Para multiplicar frações algébricas, primeiro fatoramos todos os polinômios dessas frações, depois multiplicamos os numeradores entre si e os denominadores entre si e, por fim, simplificamos a fração obtida.

Portanto, o produto das frações algébricas é calculado da mesma forma que o produto das frações normais.

A seguir, vamos ver como multiplicar duas frações algébricas com um exemplo:

$\cfrac{3x}{x^2+x-2} \cdot \cfrac{x^2-6x+5}{x+1}$

Primeiro de tudo você tem que fatorar todos os polinômios das frações, tanto os numeradores quanto os denominadores:

$\cfrac{3x}{(x-1)(x+2)} \cdot \cfrac{(x-1)(x-5)}{x+1}$

Agora vamos multiplicar frações. Para fazer isso, multiplicamos os numeradores e denominadores:

$\cfrac{3x \cdot (x-1)(x-5)}{(x-1)(x+2)\cdot (x+1)}$

$\cfrac{3x(x-1)(x-5)}{(x-1)(x+2)(x+1)}$

E por fim, simplificamos os fatores que se repetem no denominador e no numerador:

$\cfrac{3x\cancel{(x-1)}(x-5)}{\cancel{(x-1)}(x+2)(x+1)}$

O resultado da multiplicação é portanto:

$\cfrac{3x(x-5)}{(x+2)(x+1)}$

A fração não pode ser mais simplificada. Então já terminamos de multiplicar frações algébricas.

Divisão de frações algébricas

Para calcular uma divisão de frações algébricas , primeiro fatoramos todos os polinômios, depois multiplicamos as frações transversalmente (o primeiro numerador pelo segundo denominador e o primeiro denominador pelo segundo numerador) e por fim, simplificamos a fração algébrica.

Então vamos ver melhor como duas frações algébricas são divididas usando um exemplo:

$\cfrac{x^3-7x-6}{2x^2-8} : \cfrac{x^2+2x+1}{6}$

O primeiro passo para dividir duas frações algébricas é fatorar todos os polinômios envolvidos na operação:

$\cfrac{(x+1)(x+2)(x-3)}{2(x-2)(x+2)} : \cfrac{(x+1)^2}{6}$

Agora precisamos dividir as frações. Para isso, multiplicamos as frações transversalmente, ou seja, multiplica-se o primeiro numerador pelo segundo denominador e o resultado será o numerador da nova fração, e, da mesma forma, multiplica-se o primeiro denominador pelo segundo numerador e o resultado será o denominador da nova fração:

$\cfrac{(x+1)(x+2)(x-3)\cdot 6}{2(x-2)(x+2)\cdot (x+1)^2}$

$\cfrac{6(x+1)(x+2)(x-3)}{2(x-2)(x+2)(x+1)^2}$

Simplificamos os fatores que se repetem no denominador e no numerador:

$\cfrac{6\cancel{(x+1)}\cancel{(x+2)}(x-3)}{2(x-2)\cancel{(x+2)}(x+1)^\cancel{2}}$

$\cfrac{6(x-3)}{2(x-2)(x+1)}$

E podemos simplificar ainda mais a fração, já que

$6:2 = 3.$

$\cfrac{3(x-3)}{(x-2)(x+1)}$

A fração não pode ser mais simplificada. Portanto, já dividimos as frações algébricas.

Exercícios resolvidos sobre frações algébricas

A seguir oferecemos diversos exercícios resolvidos passo a passo sobre frações algébricas, para que você possa praticar e assim finalizar a compreensão do conceito. Não se esqueça que você pode nos perguntar qualquer dúvida abaixo nos comentários! 💬💬💬

Exercício 1

Determine se as seguintes frações algébricas são equivalentes ou não:

$\cfrac{x+3}{x^2-9} \qquad \cfrac{1}{x-3} \qquad \cfrac{x-3}{x^2+2x-3}$

Veja a solução

Para verificar se duas frações algébricas são equivalentes, você deve multiplicá-las transversalmente e ver se obtém uma igualdade. Portanto, primeiro verificaremos a primeira e a segunda frações:

$\cfrac{x+3}{x^2-9}= \cfrac{1}{x-3} \quad ?$

$(x+3)\cdot (x-3)=(x^2-9)\cdot 1$

Resolvemos a identidade notável à esquerda da equação:

$x^2-9=x^2-9$

✅

Neste caso, obtivemos uma igualdade, portanto a primeira e a segunda frações são algebricamente iguais.

Aplicamos agora o mesmo procedimento com a primeira e a terceira frações algébricas:

$\cfrac{x+3}{x^2-9}= \cfrac{x-3}{x^2+2x-3} \quad ?$

$(x+3)\cdot (x^2+2x-3)=(x^2-9)\cdot(x-3)$

$x^3+2x^2-3x+3x^2+6x-9=x^3-3x^2-9x+27$

$x^3+5x^2+3x-9=x^3-3x^2-9x+27$

❌

Porém, desta vez as frações algébricas não satisfazem a equação, então a primeira e a terceira frações são matematicamente diferentes.

Concluindo, a terceira fração é diferente da primeira fração e, portanto, também é desigual à segunda fração, uma vez que a primeira e a segunda frações são equivalentes.

$\cfrac{x+3}{x^2-9} = \cfrac{1}{x-3} \neq \cfrac{x-3}{x^2+2x-3}$

Exercício 2

Simplifique as seguintes frações algébricas:

$\text{A)} \ \cfrac{5x^2+10x}{11x}$

$\text{B)} \ \cfrac{x^2-4}{x^2+2x-8}$

$\text{C)} \ \cfrac{x^3-2x^2-3x}{x^2-3x}$

$\text{D)} \ \cfrac{x^3-3x+2}{x^3+4x^2+x-6}$

Veja a solução

Para simplificar uma fração algébrica, precisamos fatorar os polinômios no numerador e no denominador e, em seguida, eliminar os fatores repetidos. Ainda:

$\text{A)} \ \begin{array}{l} \cfrac{5x^2+10x}{11x} =\cfrac{5x(x+2)}{11x} = \\[4ex] =\cfrac{5\cancel{x}(x+2)}{11\cancel{x}}= \cfrac{\bm{5(x+2)}}{\bm{11}}\end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{x^2-4}{x^2+2x-8} = \cfrac{(x-2)(x+2)}{(x-2)(x+4)}= \\[4ex] = \cfrac{\cancel{(x-2)}(x+2)}{\cancel{(x-2)}(x+4)}=\cfrac{\bm{x+2}}{\bm{x+4}}}\end{array}$

$\text{C)} \ \begin{array}{l} \cfrac{x^3-2x^2-3x}{x^2-3x} = \cfrac{x(x+1)(x-3)}{x(x-3)}}= \\[4ex] = \cfrac{\cancel{x} (x+1) \cancel{x-3}}{\cancel{x}\cancel{(x-3)}} = \cfrac{x+1}{1} = \\[4ex] = \bm{x+1}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^3-3x+2}{x^3+4x^2+x-6}=\cfrac{(x-1)^2(x+2)}{(x-1)(x+3)(x+2)}= \\[4ex] = \cfrac{(x-1)^{\cancel{2}}\cancel{(x+2)}}{\cancel{(x-1)}(x+3)\cancel{(x+2)}}=\cfrac{\bm{x-1}}{\bm{x+3}}\end{array}$

Exercício 3

Calcule as seguintes adições e subtrações de frações algébricas:

$\text{A)} \ \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6}$

$\text{B)} \ \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4}$

$\text{C)} \ \cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}$

$\text{D)} \ x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}$

Veja a solução

Para somar (ou subtrair) frações algébricas, devemos primeiro reduzir as frações a um denominador comum e depois somar (ou subtrair) os numeradores. ENTÃO:

$\text{A)} \ \begin{array}{l} \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6} = \cfrac{4}{x(x+2)} + \cfrac{3x-2}{(x+2)(x-3)} = \\[4ex] =\cfrac{4\cdot(x-3)}{x(x+2)\cdot (x-3)} + \cfrac{(3x-2)\cdot x}{(x+2)(x-3)\cdot x} = \cfrac{4\cdot(x-3) + (3x-2)\cdot x}{x(x+2)(x-3)} = \\[4ex] = \cfrac{4x-12 + 3x^2-2x}{x(x+2)(x-3)} = \cfrac{ \bm{3x^2+2x-12}}{\bm{x(x+2)(x-3)}} \end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4} = \cfrac{4x}{x(x+1)^2} - \cfrac{2}{(x+1)(x-4)}= \\[4ex] = \cfrac{4x \cdot (x-4)}{x(x+1)^2 \cdot (x-4)} - \cfrac{2 \cdot (x+1) \cdot x}{(x+1)^2(x-4)\cdot x}= \cfrac{4x \cdot (x-4) - 2 \cdot (x+1) \cdot x }{x(x+1)^2 (x-4) }= \\[4ex] = \cfrac{4x^2 -16x - 2 \cdot (x^2+x) }{x(x+1)^2 (x-4) }= \cfrac{4x^2 -16x - 2x^2 - 2x }{x(x+1)^2 (x-4) } =\\[4ex] =\cfrac{2x^2 -18x}{x(x+1)^2 (x-4)}=\cfrac{x(2x -18)}{x(x+1)^2 (x-4)}= \\[4ex] = \cfrac{\bm{2x -18}}{\bm{(x+1)^2 (x-4)}}\end{array}$

$\text{C)} \ \begin{array}{l}\cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}=\cfrac{7x}{(x-2)^2} + \cfrac{-5}{x-2}} = \\[4ex] = \cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)\cdot (x-2)}=\cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)^2}= \\[4ex] = \cfrac{7x + [-5\cdot (x-2)] }{(x-2)^2} =\cfrac{7x -5\cdot (x-2) }{(x-2)^2} = \\[4ex] = \cfrac{7x -5x+10 }{(x-2)^2} = \cfrac{ \bm{2x+10}}{\bm{(x-2)^2 } } \end{array}$

$\text{D)} \ \begin{array}{l} x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}=\cfrac{x}{1} +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}= \\[4ex] =x +\cfrac{-3x}{(x-2)(x+2)} - \cfrac{2x^3-1}{2(x+1)(x+2)}= \\[4ex] = \cfrac{x\cdot 2(x-2)(x+2)(x+1)}{1\cdot 2(x-2)(x+2)(x+1)} \ + \ \cfrac{-3x\cdot 2(x+1)}{(x-2)(x+2)\cdot 2(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x+1)(x+2)\cdot (x+1)}= \\[4ex] = \cfrac{ 2x(x-2)(x+2)(x+1)}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x(x+1)}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x-2)(x+2)(x+1)}= \\[4ex]= \cfrac{ 2x^4+2x^3-8x^2-8x}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x^2-6x}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{2x^4-4x^3-x+2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - (2x^4-4x^3-x+2)}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - 2x^4+4x^3+x-2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ \bm{6x^3-14x^2-13x-2}}{\bm{2(x-2)(x+2)(x+1)}}\end{array}$

Exercício 4

Resolva as seguintes multiplicações e divisões de frações algébricas:

$\text{A)} \ \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1}$

$\text{B)} \ \cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3}$

$\text{C)} \ \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}$

$\text{D)} \ \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2}$

Veja a solução

Para multiplicar frações algébricas, devemos primeiro fatorar todos os polinômios, depois multiplicar os numeradores e denominadores e, finalmente, simplificar a fração resultante.

$\text{A)} \ \begin{array}{l} \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1} = \cfrac{(x+1)(x+4)}{7}\cdot \cfrac{x-1}{(x-1)(x+1)}\\[4ex] =\cfrac{(x+1)(x+4)\cdot (x-1)}{7 \cdot (x-1)(x+1)}=\cfrac{(x+1)(x+4) (x-1)}{7(x-1)(x+1)} = \\[4ex] = \cfrac{\cancel{(x+1)}(x+4)\cancel{ (x-1)}}{7\cancel{(x-1)}\cancel{(x+1)}} = \cfrac{\bm{x+4}}{\bm{7}}\end{array}$

$\text{B)} \ \begin{array}{l}\cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3} = \cfrac{3(x+2)(x+3)}{3x}\cdot \cfrac{(x-1)(x+2)}{(x-1)(x+1)(x+3)}= \\[4ex] =\cfrac{3(x+2)(x+3)\cdot (x-1)(x+2)}{3x\cdot (x-1)(x+1)(x+3)}=\cfrac{3(x+2)(x+3) (x-1)(x+2)}{3x (x-1)(x+1)(x+3)} = \\[4ex] = \cfrac{\cancel{3}(x+2)\cancel{(x+3)} \cancel{(x-1)}(x+2)}{\cancel{3}x \cancel{(x-1)}(x+1)\cancel{(x+3)}} = \cfrac{(x+2)(x+2)}{x (x+1)} = \\[4ex] = \cfrac{\bm{(x+2)^2}}{\bm{x (x+1)}}\end{array}$

Por outro lado, para dividir frações algébricas primeiro fatoramos todos os polinômios, depois multiplicamos as frações transversalmente (o primeiro numerador pelo segundo denominador e o primeiro denominador pelo segundo numerador) e, por fim, simplificamos a fração algébrica encontrada.

$\text{C)} \ \begin{array}{l} \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}= \cfrac{3x}{(x+5)^2}:\cfrac{2x}{(x-5)(x+5)}=\\[4ex] = \cfrac{3x\cdot (x-5)(x+5)}{(x+5)^2\cdot 2x}=\cfrac{3x(x-5)(x+5)}{2x(x+5)^2 }= \\[4ex] =\cfrac{3\cancel{x}(x-5)\cancel{(x+5)}}{2\cancel{x}(x+5)^\cancel{2}} = \cfrac{\bm{3(x-5)}}{\bm{2(x+5)}}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2} = \cfrac{(x+3)(x+5)}{4x}:\cfrac{(x-1)(x+5)}{2x^2}= \\[4ex] = \cfrac{(x+3)(x+5)\cdot 2x^2 }{4x \cdot (x-1)(x+5)} = \cfrac{2x^2 (x+3)(x+5)}{4x (x-1)(x+5)} = \\[4ex] = \cfrac{2x^{\cancel{2}}(x+3)\cancel{ (x+5)}}{4\cancel{x} (x-1)\cancel{ (x+5)}} =\cfrac{2x(x+3)}{4(x-1)} = \cfrac{\bm{x(x+3)}}{\bm{2(x-1)}}\end{array}$

O que você acha da explicação? Você gostou? Ou você tem alguma sugestão? 💬 Conte-nos o que você achou desta página nos comentários! Nós lemos todos vocês! 👀 E não se esqueça que você também pode nos tirar todas as suas dúvidas! ❔👇❔👇

Frações algébricas: simplificação, operações, exercícios resolvidos,…

O que são frações algébricas?

Equivalente de fração algébrica

Simplifique frações algébricas

Operações com frações algébricas

Adição e subtração de frações algébricas

Adicionando frações algébricas

Subtração de frações algébricas

Multiplicação de frações algébricas

Divisão de frações algébricas

Exercícios resolvidos sobre frações algébricas

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Deixe um comentário Cancelar resposta