▷ Tudo sobre geometria analítica no espaço ✅

Nesta página você encontrará a explicação de tudo sobre geometria analítica no espaço (e as fórmulas): as equações da reta e do plano, as posições relativas entre planos e retas, como distâncias e ângulos são calculados no espaço,…

O que é geometria no espaço?

A geometria espacial é o ramo da geometria responsável pelo estudo das figuras geométricas tridimensionais (3D), ou seja, aquelas que ocupam um lugar no espaço. Como o cone, o cubo, a pirâmide, a esfera, o cilindro, os prismas, os poliedros, etc.

No entanto, nesta página vamos nos concentrar na geometria analítica no espaço , a parte da geometria espacial que se concentra na análise de pontos, linhas, planos, nas distâncias entre duas figuras geométricas, no ângulo que elas formam, nos pontos de intersecção entre diferentes geometrias. figuras. elementos, etc

Equações da reta no espaço

Lembre-se de que a definição matemática de uma reta é um conjunto de pontos consecutivos representados na mesma direção, sem curvas ou ângulos.

Assim, para expressar matematicamente qualquer reta em um espaço tridimensional (em R3) utilizamos as equações da reta, e para encontrá-las precisamos apenas de um ponto que pertença à reta e ao vetor diretor dessa reta.

Com apenas esses dois elementos geométricos, você pode encontrar absolutamente todas as diferentes equações da reta, que são as seguintes:

As equações da reta são a equação vetorial , as equações paramétricas , a equação contínua e a equação implícita (ou geral) .

Abaixo você tem uma explicação dos diferentes tipos de equações da reta.

Equação vetorial da linha no espaço

Sim

$\vv{\text{v}}$

é o vetor de direção da linha e

$P$

um ponto que pertence à direita:

$\vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z) \qquad P(P_x,P_y,P_z)$

A fórmula para a equação vetorial da reta é:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=(P_x,P_y,P_z)+t\cdot (\text{v}_x,\text{v}_y,\text{v}_z) \end{empheq}$

Equações paramétricas da reta no espaço

Podemos obter a fórmula para a equação paramétrica de uma reta a partir de sua equação vetorial igualando componente a componente:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_x+t\cdot\text{v}_x \\[1.7ex] y=P_y+t\cdot\text{v}_y \\[1.7ex] z=P_z+t\cdot\text{v}_z\end{cases} \end{empheq}$

Equação contínua da reta no espaço

A fórmula para a equação contínua da reta é:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_x}{\text{v}_x}=\cfrac{y-P_y}{\text{v}_y}= \cfrac{z-P_z}{\text{v}_z} \end{empheq}$

Este tipo de equação da reta também pode ser obtida a partir de equações paramétricas, você pode ver a demonstração em nossa página da equação contínua , além disso, você também poderá ver exemplos e praticar com exercícios resolvidos de equações da direita.

Equações gerais (ou implícitas) da reta no espaço

Por fim, multiplicando as frações da equação contínua da reta duas por duas, obtemos as equações gerais (ou implícitas) da reta :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} A_1x+B_1y+C_1z+D_1=0 \\[1.7ex] A_2x+B_2y+C_2z+D_2=0\end{cases} \end{empheq}$

Este tipo de equação da reta também é chamada de equação cartesiana.

Acabamos de ver as 4 equações mais relevantes da reta (vetorial, paramétrica, contínua e geral), porém, existe outra equação um tanto particular e, portanto, é necessária uma página inteira para explicá-la. Esta é a equação canônica , neste link você pode ver toda a sua explicação, porque é tão especial e o que a diferencia de todas as outras.

Equações planas no espaço

Na geometria analítica, a equação de um plano é uma equação que permite que qualquer plano seja expresso analiticamente. Assim, para encontrar a equação de um plano, basta um ponto e dois vetores linearmente independentes pertencentes a esse plano.

Assim, todos os tipos de equações do plano são: a equação vetorial , as equações paramétricas , a equação implícita (ou geral) e a equação canônica (ou segmental) do plano.

A seguir veremos a explicação e fórmula de todas as equações do plano.

Equação vetorial do plano

Dado um ponto e dois vetores de direção de um plano:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

A fórmula para a equação vetorial de um plano é:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}} \end{empheq}$

Ou equivalente:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Ouro

$\lambda$

$\mu$

São dois escalares, ou seja, dois números reais.

Equações paramétricas do plano

Por outro lado, a fórmula para a equação paramétrica do plano é:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases} \end{empheq}$

Equação implícita ou geral do plano

A equação implícita de um plano, também chamada de equação geral, é obtida resolvendo o seguinte determinante e definindo o resultado como 0:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

Assim a equação implícita ou geral do plano resultante terá a seguinte forma:

Este tipo de equação plana também é chamada de equação plana cartesiana.

Equação canônica ou segmentar do plano

A fórmula para a equação canônica ou segmentar de um plano é a seguinte:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cfrac{x}{a}+\cfrac{y}{b} + \cfrac{z}{c} = 1 \end{empheq}$

Ouro:

$a$

Este é o ponto de intersecção entre o plano e o eixo X.
$b$

Este é o ponto de intersecção entre o plano e o eixo Y.
$c$

É aqui que o plano cruza o eixo Z.

Vetor normal a um plano

O vetor normal a um plano é um vetor perpendicular a todas as retas contidas neste plano. Portanto, um vetor normal a um plano significa que ele é perpendicular ao plano.

Muitos problemas métricos em geometria analítica espacial dizem respeito a planos e seus vetores normais. Para resolver estes exercícios basta conhecer a relação matemática entre um plano e seu vetor normal:

As componentes X, Y, Z do vetor normal a um plano coincidem respectivamente com os coeficientes A, B, C da equação implícita (ou geral) do referido plano.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Ouro

$\vv{n}$

é o vetor ortogonal ao plano

$\pi.$

Posições relativas de dois elementos geométricos no espaço

Obviamente, uma linha ou um plano não precisam necessariamente estar sozinhos no espaço, mas pelo contrário, normalmente interagem entre si: se cruzam, são paralelos, perpendiculares, etc. Bem, nesta seção veremos as diferentes posições relativas de retas e planos e como elas são determinadas.

Posição relativa de duas linhas no espaço

Na geometria analítica, ao trabalhar num espaço tridimensional (em R3) existem 4 posições relativas possíveis entre duas retas: duas retas podem ser retas coincidentes , retas paralelas , retas secantes ou retas secantes .

Linhas paralelas

Duas retas são paralelas se têm a mesma direção, mas não têm ponto em comum. Além disso, as linhas paralelas estão sempre à mesma distância umas das outras.

Linhas coincidentes

Duas retas coincidem se tiverem a mesma direção e se todos os seus pontos forem comuns.

Linhas de interseção

posição relativa de duas linhas que se cruzam

Duas linhas que se cruzam têm direções diferentes, mas se tocam em um ponto.

Linhas de interseção

Duas linhas que se cruzam têm direções diferentes e não se cruzam em nenhum ponto. Duas linhas cruzadas não estão, portanto, no mesmo plano. Por exemplo, na representação gráfica acima da linha

$s$

está sempre na frente da linha reta

$r$

, então eles nunca se tocarão.

Como encontrar a posição relativa de duas linhas por intervalos

Uma maneira de encontrar a posição relativa de duas linhas é calcular os contradomínios de duas matrizes específicas, como veremos a seguir. Este método é muito útil quando as duas retas são expressas na forma de uma equação implícita (ou geral).

Assim, se tivermos duas retas expressas com suas equações implícitas (ou gerais) em um espaço tridimensional (em R3):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

Seja A a matriz composta pelos coeficientes das duas retas:

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

E dada a matriz expandida A’, que é a matriz formada por todos os parâmetros das duas retas:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

Então, a posição relativa das duas linhas pode ser determinada pela extensão das duas matrizes anteriores de acordo com a tabela a seguir:

posições relativas de duas linhas por intervalos

Portanto, para encontrar a posição relativa entre duas linhas teremos que calcular os contradomínios de ambas as matrizes e dependendo do contradomínio de cada matriz será um caso ou outro.

Este teorema pode ser provado usando o teorema de Rouché-Frobenius (método usado para resolver sistemas de equações lineares), porém nesta página não faremos a prova porque é bastante complicado e não acrescenta muito. .

Posição relativa de dois planos no espaço

Na geometria analítica, existem apenas três posições relativas possíveis entre dois planos: planos que se cruzam, planos paralelos e planos coincidentes.

Planos que se cruzam : dois planos estão se cruzando se apenas se cruzarem em uma linha.
Planos paralelos : Dois planos são paralelos se não se cruzam em nenhum ponto.
Planos coincidentes : dois planos são coincidentes se tiverem todos os pontos em comum.

Fotos que se cruzam

posição relativa de dois planos que se cruzam

planos paralelos

Planos correspondentes

posição relativa de dois planos coincidentes

Como determinar a posição relativa de dois planos por coeficientes

Uma forma de saber a posição relativa entre dois planos é utilizar os coeficientes de suas equações gerais (ou implícitas).

Considere então a equação geral (ou implícita) de dois planos diferentes:

$\pi_1 : \ Ax+By+Cz+D=0$

$\pi_2 : \ A'x+B'y+C'z+D'=0$

A posição relativa entre os dois planos num espaço tridimensional depende da proporcionalidade dos seus coeficientes ou parâmetros:

posição relativa de dois planos com parâmetros

Assim, os dois planos se cruzarão quando um dos coeficientes A, B ou C não for proporcional aos demais. Por outro lado, os dois planos serão paralelos quando apenas os termos independentes não forem proporcionais. E, finalmente, os planos coincidirão quando todos os coeficientes das duas equações forem proporcionais.

Distâncias no espaço

Abaixo você encontra as fórmulas para calcular a distância entre diferentes elementos geométricos: entre um ponto e uma reta, entre dois planos, entre um plano e uma reta,…

Distância entre dois pontos

A distância entre dois pontos corresponde à norma do vetor determinado por estes 2 pontos.

Então, se tivermos dois pontos genéricos:

$A(a_x,a_y,a_z) \qquad \qquad B(b_x,b_y,b_z)$

A fórmula para a distância entre os dois pontos é:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(A,B) = \vert \vv{AB} \rvert = \sqrt{(b_x-a_x)^2+(b_y-a_y)^2+(b_z-a_z)^2} \end{empheq}$

Distância de um ponto a uma reta

A fórmula para calcular a distância de um ponto a uma linha no espaço é:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert} \end{empheq}$

Ouro:

$\lvert \vv{\text{v}}_r \rvert$

é o módulo do vetor de direção da linha

$r.$
$Q$

é um ponto à direita

$r,$

$P$

um ponto na linha

$s$

E

$\vv{QP}$

o vetor definido pelos dois pontos
$\lvert \vv{QP} \times \vv{\text{v}}_r \rvert$

é o módulo do produto vetorial entre os vetores

$\vv{QP}$

E

$\vv{\text{v}}_r$

Distância entre duas linhas

A distância entre duas linhas depende de sua posição relativa:

Se as duas retas coincidem ou se cruzam , a distância entre as duas retas é igual a zero, pois elas se cruzam (pelo menos) em um ponto.
Quando as duas retas são paralelas ou se cruzam, deve-se aplicar uma fórmula dependendo do caso (ambas as explicações estão disponíveis abaixo).

Distância entre duas linhas paralelas

Duas linhas paralelas estão sempre à mesma distância. Então para calcular a distância entre duas retas paralelas no espaço (em R3) isso é feito da mesma forma que no plano (em R2): basta pegar um ponto em uma das duas retas e encontrar a distância aí é deste ponto até a outra linha.

Portanto, para determinar a distância entre 2 retas paralelas você deve usar a fórmula da distância entre um ponto e uma reta.

Distância entre duas linhas que se cruzam

Seja o vetor de direção e qualquer ponto de duas linhas que se cruzam:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}$

A fórmula para a distância entre duas linhas que se cruzam é:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} \end{empheq}$

Ouro:

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|$

é o valor absoluto do produto misto dos vetores

$\vv{\text{u}}, \vv{\text{v}}$

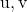
e o vetor definido pelos pontos

$A$

E

$B$

.
$\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert$

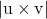
é o módulo do produto vetorial entre os vetores de direção das duas linhas cruzadas.

Embora você tenha a fórmula aqui, determinar a distância entre duas linhas que se cruzam é mais complicado do que parece. Então se quiser praticar no link a seguir você pode ver exemplos e exercícios resolvidos sobre adistância entre duas linhas que se cruzam.

Distância de um ponto a um plano

Dado um ponto e a equação geral (ou implícita) de um plano:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

A fórmula para a distância de um ponto a um plano é:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}} \end{empheq}$

qual é a distância de um ponto a um plano

Se aplicando a fórmula obtivemos um resultado igual a zero, isso obviamente significa que a distância entre o ponto e o plano é zero e, portanto, o ponto faz parte deste plano.

Distância entre dois planos

A distância entre dois planos no espaço depende da posição relativa entre estes dois planos:

Se os dois planos se cruzam ou coincidem , a distância entre eles é igual a zero porque se cruzam num determinado ponto.
Se os dois planos forem paralelos , a distância entre os dois planos é calculada tomando um ponto em um dos dois planos e calculando a distância entre esse ponto e o outro plano.

Distância entre dois planos paralelos

Dois planos paralelos estão sempre à mesma distância um do outro, portanto, para determinar a distância entre dois planos paralelos, podemos pegar num ponto num dos dois planos e calcular a distância desse ponto ao outro plano.

Portanto, para calcular a distância entre dois planos paralelos, você deve encontrar um ponto em um dos dois planos e, em seguida, usar a fórmula da distância entre um ponto e um plano.

Ângulos no espaço

Tal como acontece com as distâncias, a determinação do ângulo entre dois objetos geométricos no espaço depende de suas características geométricas. Porque calcular o ângulo formado por duas retas não é a mesma coisa que calcular o ângulo formado por dois planos. Abaixo você tem as fórmulas para encontrar os ângulos entre retas e planos.

Ângulo entre duas linhas

Para saber o ângulo entre duas retas no espaço euclidiano, devemos calcular o ângulo formado pelos seus vetores diretores, portanto:

Dados os vetores de direção de duas linhas diferentes:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y,\text{u}_z)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y,\text{v}_z)$

O ângulo formado por essas duas linhas pode ser calculado com a seguinte fórmula:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

Ouro

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

são os módulos dos vetores

$\vv{\text{u}}$

$\vv{\text{v}}$

respectivamente.

Lembre-se de que a fórmula do módulo de um vetor é:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

Ângulo entre dois planos

O ângulo entre dois planos é igual ao ângulo formado pelos vetores normais desses planos. Portanto, para encontrar o ângulo entre dois planos, calculamos o ângulo formado pelos seus vetores normais, uma vez que são equivalentes .

Dada a equação geral (ou implícita) de dois planos diferentes:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1=0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2=0$

O vetor normal de cada plano é:

$\vv{n}_1=(A_1,B_1,C_1)$

$\vv{n}_2=(A_2,B_2,C_2)$

E o ângulo formado por esses dois planos é determinado calculando o ângulo formado por seus vetores normais usando a seguinte fórmula:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{n}_1 \cdot \vv{n}_2\rvert}{\lvert \vv{n}_1 \rvert \cdot \lvert \vv{n}_2 \rvert} \end{empheq}$

Ângulo entre uma reta e um plano

O ângulo formado por uma reta e um plano é definido como o menor dos dois ângulos complementares formados pelo vetor diretor da reta e pelo vetor normal do plano.

Portanto, se

$\vv{\text{v}}$

é o vetor de direção da linha e

$\vv{n}$

é o vetor normal ao plano:

$\vv{\text{v}} = (\text{v}_x,\text{v}_y,\text{v}_z)$

$\vv{n}=(n_x,n_y,n_z)$

A fórmula usada para calcular o ângulo formado por uma linha e um plano é:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \text{sen}(\alpha)=\cfrac{\lvert \vv{\text{v}} \cdot \vv{n}\rvert}{\lvert \vv{\text{v}} \rvert \cdot \lvert \vv{n} \rvert} \end{empheq}$

Geometria analítica no espaço (fórmulas)

O que é geometria no espaço?

Equações da reta no espaço

Equação vetorial da linha no espaço

Equações paramétricas da reta no espaço

Equação contínua da reta no espaço

Equações gerais (ou implícitas) da reta no espaço

Equações planas no espaço

Equação vetorial do plano

Equações paramétricas do plano

Equação implícita ou geral do plano

Equação canônica ou segmentar do plano

Vetor normal a um plano

Posições relativas de dois elementos geométricos no espaço

Posição relativa de duas linhas no espaço

Como encontrar a posição relativa de duas linhas por intervalos

Posição relativa de dois planos no espaço

Como determinar a posição relativa de dois planos por coeficientes

Distâncias no espaço

Distância entre dois pontos

Distância de um ponto a uma reta

Distância entre duas linhas

Distância entre duas linhas paralelas

Distância entre duas linhas que se cruzam

Distância de um ponto a um plano

Distância entre dois planos

Distância entre dois planos paralelos

Ângulos no espaço

Ângulo entre duas linhas

Ângulo entre dois planos

Ângulo entre uma reta e um plano

Deixe um comentário Cancelar resposta