▷ Como calcular o ponto médio de um segmento? (Fórmula)

Esta página explica o significado do ponto médio de um segmento. Além disso, você descobrirá como encontrar o meio de um segmento usando sua fórmula. Você ainda verá exemplos, exercícios e problemas resolvidos de pontos médios de segmentos.

Qual é o ponto médio de um segmento?

Em matemática, o ponto médio de um segmento é o ponto localizado à mesma distância das extremidades de um segmento. O meio, portanto, divide o segmento em duas partes iguais.

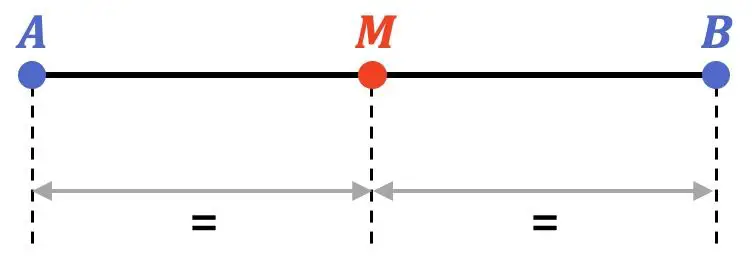
Além disso, o ponto médio está bem no centro do segmento, portanto pertence à bissetriz do segmento.

Por outro lado, o ponto médio de um segmento é também um ponto equidistante de dois elementos geométricos: as duas extremidades do segmento.

Como calcular o ponto médio de um segmento?

Dadas as coordenadas cartesianas dos pontos extremos de um segmento:

$A(x_1,y_1) \qquad B(x_2,y_2)$

As coordenadas do meio do referido segmento correspondem à meia soma das coordenadas dos pontos extremos:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

Esta é a fórmula para o meio de um segmento no plano cartesiano (em R2). Mas obviamente a fórmula também é aplicável ao espaço cartesiano (em R3), bastando somar a meia soma da coordenada Z:

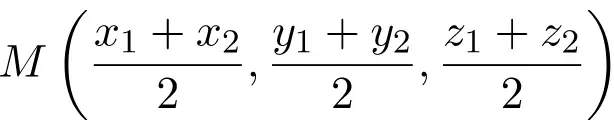
Vejamos um exemplo de como calcular as coordenadas do ponto médio de um segmento:

Determine o ponto médio do segmento formado pelos seguintes pontos:

$A(2,5) \qquad B(4,-1)$

Para encontrar o meio do segmento, basta aplicar sua fórmula:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{2+4}{2} , \frac{5+(-1)}{2} \right)$

$\displaystyle M\left(\frac{6}{2} , \frac{4}{2} \right)$

$\displaystyle \bm{M\left(3,2\right)}$

Exercícios resolvidos no meio de um segmento

Exercício 1

Qual é o ponto médio do segmento cujas extremidades são os dois pontos seguintes?

$A(3,-2) \qquad B(5,8)$

Veja a solução

Para encontrar o meio do segmento você deve aplicar diretamente a fórmula:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{3+5}{2} , \frac{-2+8}{2} \right)$

$\displaystyle M\left(\frac{8}{2} , \frac{6}{2} \right)$

$\displaystyle \bm{M\left(4,3\right)}$

Exercício 2

Encontre as coordenadas do ponto final do segmento que começa no ponto A e cujo ponto médio é M.

$A(4,-1) \qquad M(-2,1)$

Veja a solução

Neste caso conhecemos as coordenadas do ponto inicial e do meio do segmento. Portanto, substituímos as coordenadas que conhecemos na fórmula do ponto médio de um segmento:

$\displaystyle \left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)=(x_m,y_m)$

$\displaystyle \left(\frac{4+x_2}{2} , \frac{-1+y_2}{2} \right)=(-2,1)$

E agora resolvemos as coordenadas do ponto final do segmento da equação anterior:

Coordenadas X

$\cfrac{4+x_2}{2} = -2$

$4+x_2 = -2 \cdot 2$

$4+x_2 = -4$

$x_2 = -4-4$

$x_2 = -8$

Coordenadas Y

$\cfrac{-1+y_2}{2} = 1$

$-1+y_2 = 1 \cdot 2$

$-1+y_2 = 2$

$y_2 = 2+1$

$y_2 = 3$

As coordenadas da extremidade final do segmento são, portanto:

$\bm{B(-8,3)}$

Exercício 3

Dado o seguinte paralelogramo:

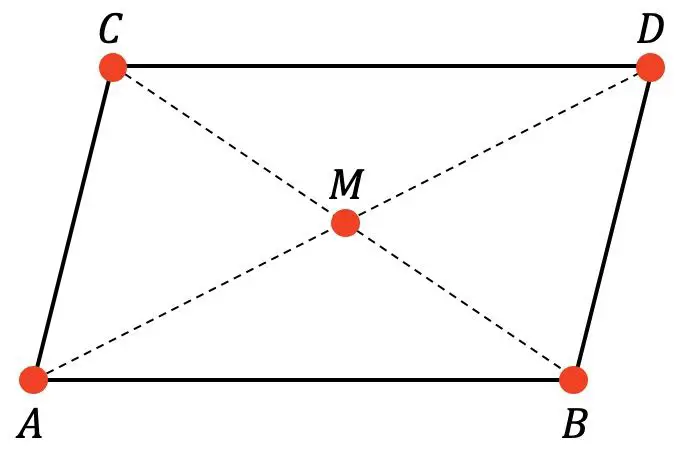
Sabemos que M é o centro do paralelogramo e as coordenadas dos pontos A, B e C são:

$A(1,1) \quad B(5,1) \quad C(7,3)$

A partir dessas informações e utilizando a fórmula do ponto médio, calcule as coordenadas do ponto D.

Veja a solução

Para encontrar as coordenadas do ponto D usando a fórmula do meio de um segmento, você deve primeiro calcular as coordenadas do ponto M e depois as do ponto D.

O ponto M é o ponto médio do segmento BC, suas coordenadas são portanto:

$\displaystyle M\left(\frac{5+7}{2} , \frac{1+3}{2} \right)$

$\displaystyle M\left(6,2 \right)$

E uma vez conhecido o ponto M, podemos encontrar o ponto D. O ponto M também é o meio do segmento AD, então:

$\displaystyle \left(\frac{1+x_2}{2} , \frac{1+y_2}{2} \right)=(6,2)$

Coordenada X do ponto D

$\cfrac{1+x_2}{2} = 6$

$1+x_2 = 12$

$x_2 = 11$

Coordenada Y do ponto D

$\cfrac{1+y_2}{2} = 2$

$1+y_2 = 4$

$y_2 = 3$

As coordenadas do ponto D são, portanto:

$\bm{D(11,3}$

Exercício 4

Calcule a equação contínua da reta perpendicular ao segmento PQ em seu ponto médio. Seja os pontos

$P(1,4)$

$Q(5,-2).$

Veja a solução

Para determinar a equação de uma reta, precisamos de seu vetor diretor e de um ponto que faz parte da reta.

Neste caso, o vetor de direção da reta será perpendicular ao vetor

$\vv{PQ}.$

Portanto, calculamos o vetor

$\vv{PQ}:$

$\vv{PQ} = Q - P = (5,-2)-(1,4) = (4,-6)$

E podemos encontrar um vetor perpendicular a outro alterando as componentes do vetor entre eles e depois alterando o sinal de uma componente, portanto:

$\vv{PQ}_\perp =(6,4)$

Agora temos o vetor diretor da reta, então precisamos apenas de um ponto pertencente à reta. Neste caso, a instrução nos diz que a reta passa pelo ponto médio do segmento, então calculamos o ponto médio usando a fórmula:

$\displaystyle M\left(\frac{1+5}{2} , \frac{4+(-2)}{2} \right)$

$\displaystyle M\left(3,1 \right)$

Finalmente, construímos a equação contínua da reta a partir do ponto e vetor calculados:

$\cfrac{x-3}{6}=\cfrac{y-1}{4}$

Fórmula para o meio de um segmento

Qual é o ponto médio de um segmento?

Como calcular o ponto médio de um segmento?

Exercícios resolvidos no meio de um segmento

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Deixe um comentário Cancelar resposta