Fórmula para distância entre dois pontos (geometria)

Nesta página você descobrirá como calcular a distância entre dois pontos na geometria (fórmula). Você também poderá ver exemplos e, além disso, praticar com exercícios resolvidos a distância entre dois pontos.

Qual é a fórmula para a distância entre dois pontos?

A distância entre dois pontos é igual ao comprimento do segmento que os une. Portanto, em matemática, para determinar a distância entre dois pontos diferentes, devemos calcular os quadrados das diferenças entre as suas coordenadas e depois encontrar a raiz da soma desses quadrados.

Em outras palavras, a fórmula utilizada para calcular a distância entre dois pontos diferentes no plano cartesiano é a seguinte:

Considere as coordenadas de dois pontos distintos:

$A(x_1,y_1) \qquad \qquad B(x_2,y_2)$

A fórmula para a distância entre dois pontos é:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Esta fórmula vem da magnitude de um vetor. Na verdade, o que estamos fazendo com esta fórmula é calcular a norma do vetor que é determinada pelos dois pontos em questão. Você pode ler mais sobre isso na explicação do que é o módulo de um vetor .

Por outro lado, em geometria analítica a demonstração da fórmula da distância entre dois pontos também pode ser feita através do teorema de Pitágoras:

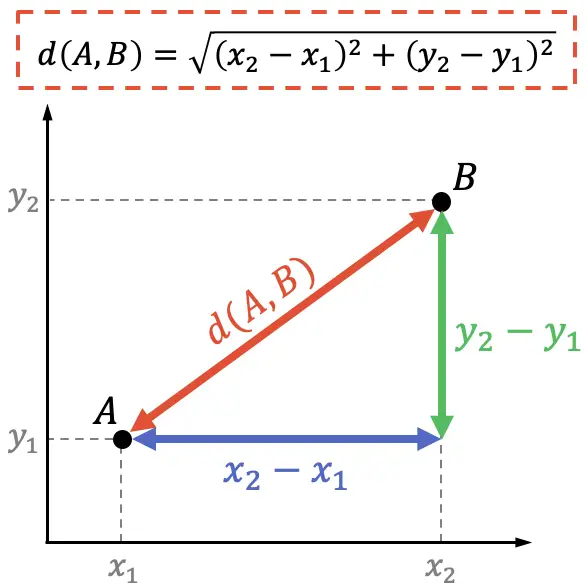
fórmula para a distância entre dois pontos

O teorema de Pitágoras afirma que o quadrado da hipotenusa de um triângulo retângulo é equivalente à soma dos quadrados de seus catetos, portanto:

$\bigl(d(A,B)\bigr)^2 = (x_2-x_1)^2 + (y_2-y_1)^2$

E para obter a fórmula basta encontrar a distância entre os 2 pontos:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Por fim, vale ressaltar que, se estivéssemos trabalhando com pontos de 3 coordenadas, a fórmula da distância entre dois pontos no espaço (em R3) seria a mesma, mas somando a coordenada Z:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2 \vphantom{\frac{1}{2}}}$

Exemplo de cálculo da distância entre dois pontos

Depois de vermos a definição da fórmula da distância entre dois pontos, vamos agora ver como determinar essa distância usando um exemplo:

Encontre a distância entre os dois pontos a seguir:

$A(-1,7) \qquad \qquad B(3,4)$

Para encontrar geometricamente a distância entre os dois pontos, basta aplicar a fórmula:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Agora substituímos as coordenadas dos pontos na fórmula:

$d(A,B) = \sqrt{(3-(-1))^2+(4-7)^2 \vphantom{\frac{1}{2}}}$

E fazemos os cálculos:

$\begin{aligned} d(A,B) &= \sqrt{(3+1)^2+(4-7)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{4^2+(-3)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{16+9}\\[2ex] &= \sqrt{25}\\[2ex] & = \bm{5}\end{aligned}$

A distância entre os dois pontos é, portanto, igual a 5 unidades.

Obviamente, o valor da distância deve sempre dar-nos um sinal positivo, porque as distâncias são sempre positivas. Caso contrário, significa que cometemos um erro em uma etapa.

Solução de problemas de distância entre dois pontos

Exercício 1

Calcule a distância entre os dois pontos a seguir:

$A(4,2) \qquad \qquad B(1,5)$

veja solução

Para encontrar a distância geométrica entre os dois pontos, basta usar a fórmula:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Agora substituímos as coordenadas dos pontos na fórmula:

$d(A,B) = \sqrt{(1-4)^2+(5-2)^2 \vphantom{\frac{1}{2}}}$

E fazemos os cálculos:

$\begin{aligned} d(A,B) & = \sqrt{(-3)^2+3^2 } \\[2ex] & = \sqrt{9+9 } \\[2ex] & = \bm{\sqrt{18}} \end{aligned}$

Exercício 2

Encontre a distância entre os dois pontos a seguir:

$A(8,6) \qquad \qquad B(-4,1)$

veja solução

Para encontrar a distância matemática entre os dois pontos, devemos usar a fórmula correspondente:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Agora substituímos as coordenadas dos pontos na fórmula:

$d(A,B) = \sqrt{(-4-8)^2+(1-6)^2 \vphantom{\frac{1}{2}}}$

E fazemos os cálculos:

$\begin{aligned} d(A,B) &= \sqrt{(-12)^2+(-5)^2 } \\[2ex] &= \sqrt{144+25 }\\[2ex] &= \sqrt{169} \\[2ex] &= \bm{13}\end{aligned}$

Exercício 3

Calcule o perímetro do triângulo formado pelos pontos A, B e C mostrados graficamente abaixo:

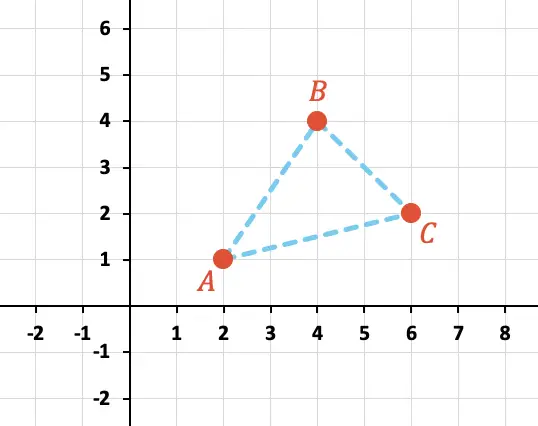
exercício resolvido da distância entre dois pontos

veja solução

Primeiro, precisamos identificar as coordenadas X e Y de cada ponto do gráfico:

$A(2,1)$

$B(4,4)$

$C(6,2)$

E agora precisamos calcular a distância entre todos os pontos com a fórmula:

$d(A,B) = \sqrt{(4-2)^2+(4-1)^2 } = \sqrt{4+9} =\sqrt{13} = 3,61$

$d(A,C) = \sqrt{(6-2)^2+(2-1)^2 } = \sqrt{16+1} =\sqrt{17} = 4,12$

$d(B,C) = \sqrt{(6-4)^2+(2-4)^2 } = \sqrt{4+4} =\sqrt{8} = 2,83$

Portanto, o perímetro do triângulo será a soma dos comprimentos dos 3 lados:

$P=3,61+4,12+2,83= \bm{10,56}$

Exercício 4

Verifique se o triângulo cujos vértices são os pontos A, B e C é um triângulo isósceles. Mas os três pontos:

$A(-4,5) \qquad B(7,-5) \qquad C(10,0)$

veja solução

Para que um triângulo seja isósceles, dois de seus lados devem ser iguais. Devemos, portanto, encontrar o comprimento de cada um dos seus lados, que corresponde às distâncias entre os seus vértices.

Portanto, calculamos a distância entre os vértices do triângulo:

$d(A,B) = \sqrt{(7-(-4))^2+(-5-5)^2 } = \sqrt{11^2+(-10)^2} = \sqrt{221}$

$d(A,C) = \sqrt{(10-(-4))^2+(0-5)^2 } = \sqrt{14^2+(-5)^2} = \sqrt{221}$

$d(B,C) = \sqrt{(10-7)^2+(0-(-5))^2} = \sqrt{3^2+5^2} = \sqrt{34}$

Portanto, o triângulo tem 2 lados idênticos e o terceiro lado mede de forma diferente dos outros dois, então é efetivamente um triângulo isósceles.

Exercício 5

Encontre um ponto no eixo Y que seja equidistante dos dois pontos a seguir:

$A(5,-3) \qquad \qquad B(-2,4)$

veja solução

Em primeiro lugar, se o ponto estiver localizado no eixo do computador (eixo OY), isso significa que a abcissa do ponto é zero:

$P(0,y)$

Segundo, se o ponto for equidistante dos pontos A e B, isso implica que a seguinte equação é satisfeita:

$d(P,A)= d(P,B)$

Assim, utilizando a fórmula da distância entre dois pontos, podemos encontrar o valor da variável y da equação anterior:

$\sqrt{(5-0)^2+(-3-y)^2 \vphantom{\frac{1}{2}}}=\sqrt{(-2-0)^2+(4-y)^2 \vphantom{\frac{1}{2}}}$

Como ambos os lados da equação têm raiz, podemos simplificá-los:

$5^2+(-3-y)^2=(-2)^2+(4-y)^2$

Resolvemos as potências e igualdades notáveis (ou produtos notáveis):

$25+9+y^2+6y=4+16+y^2-8y$

E operamos até encontrarmos o valor da incógnita y :

$y^2+6y-y^2+8y=4+16-25-9$

$14y=-14$

$y=\cfrac{-14}{14}$

$y=-1$

Resumindo, o ponto que a declaração do problema nos perguntou é:

$\bm{P(0,-1)}$

Se você achou este artigo útil, provavelmente também se interessará por exercícios sobre a distância entre um ponto e uma reta . Na página vinculada você encontrará não apenas exercícios resolvidos passo a passo, mas também uma explicação detalhada do cálculo da distância entre pontos e retas, exemplos e aplicação da fórmula da distância entre um ponto e uma reta para determinar outro tipo de distância .

Qual é a fórmula para a distância entre dois pontos?

Exemplo de cálculo da distância entre dois pontos

Solução de problemas de distância entre dois pontos

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Deixe um comentário Cancelar resposta