A fórmula de Euler é um conceito matemático que liga dois conceitos elementares da matemática: números complexos e trigonometria. Isso a torna uma das conceituações mais importantes e com mais aplicações em toda a matemática. Ao longo deste artigo veremos como é essa fórmula e todos os usos que ela tem.
Qual é a fórmula de Euler?
A fórmula de Euler é uma equação matemática fundamental baseada no número de Euler , que relaciona números complexos à trigonometria. Foi descoberto pelo matemático suíço Leonhard Euler no século 18 e desde então tem sido usado em diversos campos, da física à ciência da computação.
A fórmula de Euler é escrita como e ix = cos(x) + i sin(x) , onde e é a base do logaritmo natural, i é a unidade imaginária (definida como a raiz quadrada de -1) e x é um real número. Esta equação especifica que o número complexo e ix é igual à soma do número real cos(x) e o produto do número imaginário i pelo número real sin(x).

A importância da fórmula de Euler reside no fato de permitir que números complexos sejam expressos em termos de números reais e trigonometria, tornando-os mais fáceis de manipular e calcular.
Prova da fórmula de Euler
A prova da fórmula de Euler é baseada no uso da série de Taylor para a função exponencial e na identidade trigonométrica para cosseno e seno.
Primeiro, consideramos a série de Taylor para a função exponencial:

A seguir, substituímos x por ix na equação acima, onde i é a unidade imaginária (raiz quadrada de -1):
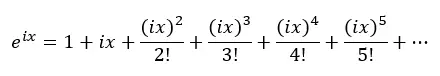
Então, aplicamos as potências de i e substituímos na equação anterior:
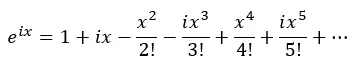
Agora agrupamos os termos reais e os termos com i:
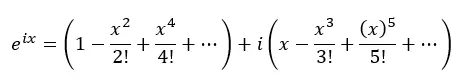
Na verdade, cada um dos parênteses acima é a série de Taylor para cosseno e seno:
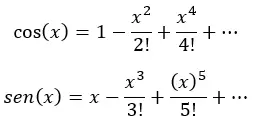
Finalmente, simplificamos (substituindo cada expressão entre parênteses por cosseno e seno de x) e obtemos:

Exemplo da fórmula de Euler
Agora que você já sabe como funciona essa fórmula matemática, recomendamos tentar resolver o seguinte exemplo prático: Expresse o número complexo e 2i (em radianos) na forma binomial:
A principal aplicação da fórmula de Euler é converter um número complexo expresso na forma exponencial em forma binomial. Portanto, usaremos a fórmula : e ix = cos(x) + i sin(x)
e 2i = cos(2) + i sin(2)
e2i = -0,416 + 0,909i
E já teríamos o número na forma binomial. A partir daí podemos fazer a representação gráfica no plano complexo . Para isso, é necessário entender que um número complexo é representado no plano complexo usando como coordenadas a parte real na abcissa (eixo x) e a parte imaginária na ordenada (eixo y).
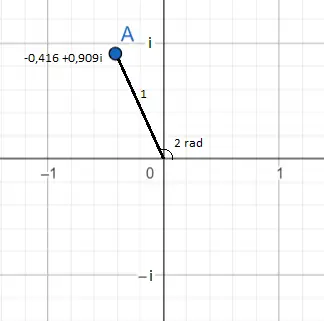
Na imagem anterior é mostrado o número complexo e 2i , que é igual a -0,416 + 0,909i. Isso pode ser visto como um ponto azul. Sua localização no avião pode ser vista de dois ângulos .
A primeira e mais óbvia é com a representação do número na forma binomial : -0,416 (na abcissa) e 0,909 (no computador). E a segunda está na forma exponencial : o módulo de e 2i é igual a 1, pois é o número que está na frente de e (como não existe número na frente de e, devemos imaginar que se existe um 1) e no expoente há 2, portanto, o argumento ou ângulo equivale a dois radianos.
Se você não entendeu muito bem este último parágrafo , recomendamos que leia nosso artigo sobre números complexos. Bom, aí fazemos uma explicação bem aprofundada das diferentes formas de escrever um número complexo e de todas as suas propriedades.
Representação gráfica da fórmula de Euler
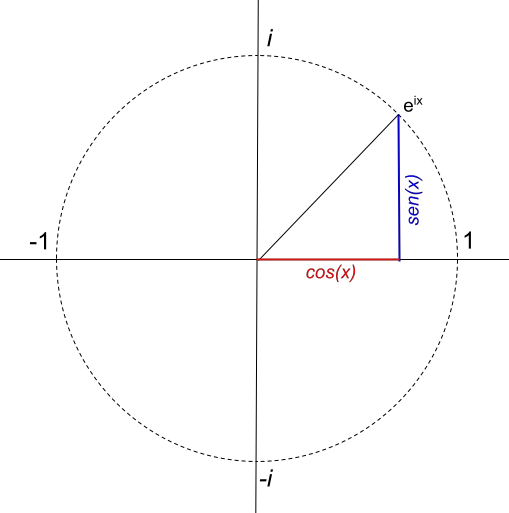
No exemplo anterior, você pôde ver como a fórmula de Euler é aplicada e como ela é representada graficamente no plano complexo. Mas, se formos um pouco mais longe e tentarmos representar uma função equivalente à fórmula de Euler, encontramos algo muito curioso: ela gera um círculo de raio 1 :
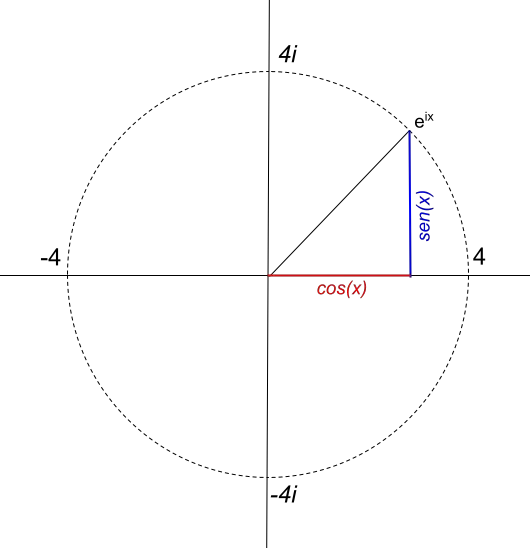
Porém, o raio do círculo depende diretamente do valor do módulo do número complexo. Por exemplo, se quisermos representar um círculo com raio 4, a função será 4e ix . Então, a função 4e ix é representada assim:
Voltando ao círculo de raio 1, se decidirmos representar e iπ (em radianos), devemos primeiro calcular:
e πi = cos(π) + i sin(π)
eπi = -1 + eu 0
eπi = -1
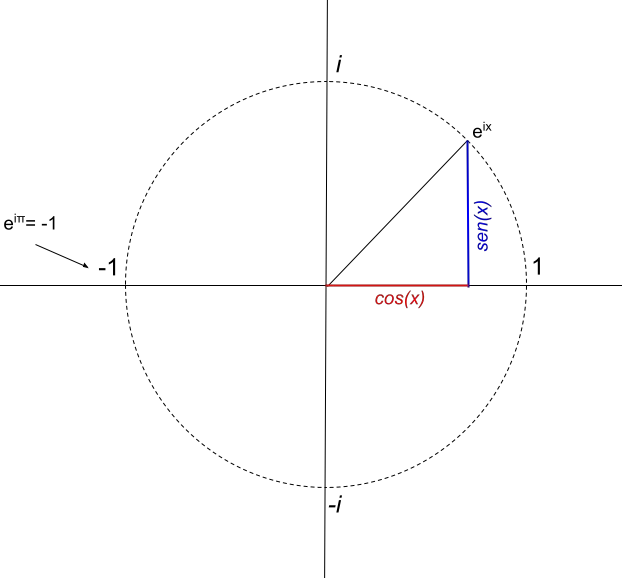
Obtemos e πi = -1, que é a famosa identidade de Euler.
Deduzimos disso que o número complexo e πi possui apenas uma parte real, que é igual a -1. Portanto, sua representação seria tal que:
Aplicações da fórmula de Euler
- Números complexos: a fórmula de Euler é uma relação entre funções trigonométricas e números complexos. A partir desta fórmula, podemos expressar números complexos de diferentes maneiras: binomial, exponencial e polar.
- Série de Taylor: a fórmula de Euler é usada para estender funções da série de Taylor.
- Álgebra Linear: A fórmula de Euler é usada na diagonalização de matrizes, que é uma técnica fundamental em álgebra linear.
- Cálculo Diferencial e Integral: A fórmula de Euler é utilizada na solução de equações diferenciais, sendo uma técnica relevante em cálculo.
Além disso, tem aplicações em muitas teorias matemáticas e até mesmo em conceitos fora do domínio matemático, como teoremas de física.
conclusões
Como você viu neste artigo, a maior aplicação da fórmula de Euler está nos números complexos : na sua expressão numérica e na sua representação. É verdade que isso tem alguma aplicação em álgebra, mas essencialmente você está trabalhando com números complexos. Portanto, é importante compreendê-los bem, acima de tudo.
Dito isto, esperamos ter ajudado você a entender melhor esse conceito. E se você tiver alguma dúvida ou não souber fazer algum exercício, não hesite em nos escrever nos comentários.