Inclinação de uma linha (fórmula)

Nesta página você encontrará a explicação mais detalhada da inclinação de uma reta: qual é sua fórmula, exemplos de cálculo, o que significa o conceito de inclinação de uma reta,… Você também poderá ver como identificar facilmente a inclinação de uma reta a partir de sua equação e, além disso, poderá praticar com exercícios resolvidos passo a passo.

Fórmula para a inclinação de uma linha

A inclinação de uma linha é igual ao deslocamento vertical entre dois pontos dividido pelo deslocamento horizontal entre esses mesmos dois pontos.

Isto é, dados dois pontos em uma linha:

$P_1(x_1,y_1) \qquad P_2(x_2,y_2)$

A fórmula para a inclinação de uma linha é:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

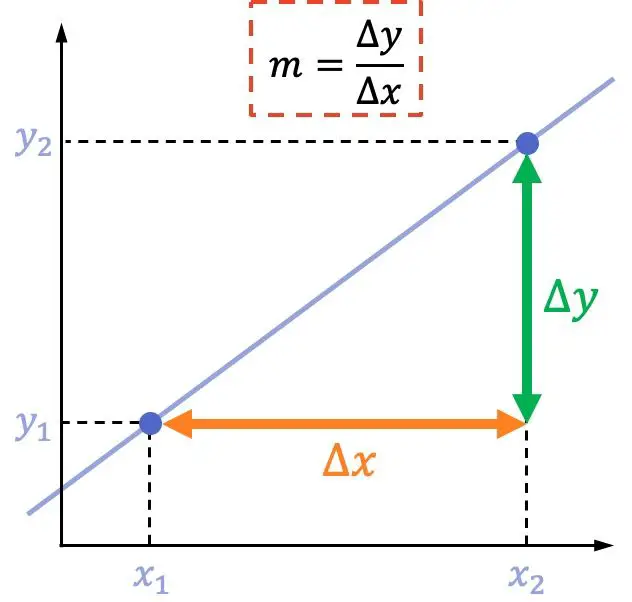
Exemplo de cálculo da inclinação de uma linha a partir de dois pontos

A seguir, veremos um exemplo de como a inclinação de uma reta é calculada com a fórmula:

Calcule a inclinação da reta que passa pelos dois pontos a seguir:

$P_1(3,1) \qquad P_2(5,7)$

Para encontrar a inclinação desta reta, basta aplicar sua fórmula:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{7-1}{5-3}=\cfrac{6}{2} = \bm{3}$

A inclinação da linha é, portanto, igual a 3.

Encontrar a inclinação de uma reta a partir de sua equação

Na seção acima, vimos como determinar numericamente a inclinação de uma reta. Porém, nem sempre é necessário fazer cálculos, mas seu valor também pode ser identificado a partir da equação de uma reta. Cada tipo de equação é diferente, por isso analisaremos cada caso separadamente.

Inclinação dada a equação explícita da reta

A equação explícita da reta segue a seguinte expressão:

$y =\color{blue}\bm{m}\color{black}x+n$

Então o parâmetro

$m$

corresponde à inclinação da linha.

Inclinação dada a equação ponto-inclinação da reta

A fórmula para a equação ponto-inclinação da reta é a seguinte:

$y -y_0=\color{blue}\bm{m}\color{black}(x-x_0)$

Como antes, o coeficiente

$m$

corresponde à inclinação da linha.

Inclinação dada a equação implícita da reta

Dada a equação implícita da reta (também chamada de equação geral ou cartesiana):

$Ax+By+C=0$

A inclinação da linha pode ser encontrada fazendo:

$m=-\cfrac{A}{B}$

Inclinação levando em consideração o vetor de direção da linha

O vetor de direção da linha é o vetor que marca sua direção. Então, se o vetor diretor de uma reta for:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

A inclinação desta reta é:

$m=\cfrac{\text{v}_2}{\text{v}_1}$

inclinação dado um ângulo

Finalmente, se uma linha forma um ângulo

$\alpha$

na parte positiva do eixo das abcissas (eixo X), sua inclinação é equivalente à tangente do ângulo:

$m = \text{tg}(\alpha)$

Significado da inclinação de uma linha

Com todas as informações acima, já sabemos perfeitamente como encontrar a inclinação de uma reta. Mas realmente… o que significa a inclinação de uma linha?

A inclinação de uma linha indica as unidades verticais que a linha sobe para cada unidade horizontal do gráfico.

Por exemplo, na representação da linha a seguir, você pode ver que ela avança 2 unidades verticais para cada unidade horizontal, pois sua inclinação é igual a 2.

Além disso, a inclinação de uma linha também indica a sua inclinação:

Se uma linha está aumentando (subindo), sua inclinação é positiva.
Se uma linha estiver decrescendo (descendente), sua inclinação será negativa.
Se uma linha for completamente horizontal, sua inclinação será igual a 0.
Se uma linha for completamente vertical, sua inclinação será igual ao infinito.

inclinação de uma linha positiva ou negativa

inclinação de uma linha zero ou infinita

Posição relativa das linhas

Por outro lado, a posição relativa entre duas linhas também pode ser conhecida a partir das propriedades das inclinações:

Se duas retas possuem inclinações diferentes, isso significa que elas se cruzam , ou seja, se cruzam em um ponto.

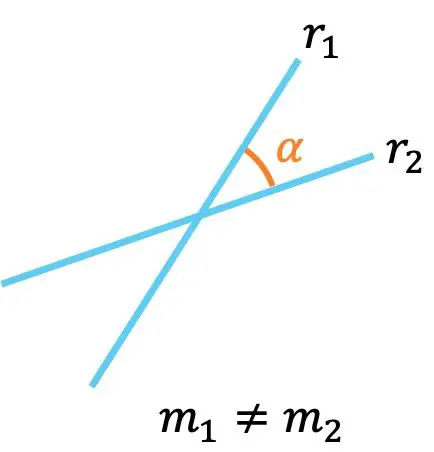
Além disso, o ângulo entre as duas linhas em suas inclinações pode ser calculado com a seguinte fórmula:

$\text{tg}(\alpha) = \cfrac{m_2-m_1}{1+m_1\cdot m_2}$

Em segundo lugar, se duas retas têm a mesma inclinação, isso implica que são paralelas .

Finalmente, as inclinações de duas linhas perpendiculares ou ortogonais (que formam 90º) atendem à seguinte condição:

linhas perpendiculares opostas às encostas

Esta é uma forma de descobrir se duas retas são paralelas ou perpendiculares entre si, porém, existem outros métodos e alguns são ainda mais rápidos. Para saber mais você pode ir para a explicação da perpendicularidade e paralelismo entre linhas . Além disso, estas páginas também explicam como encontrar uma linha perpendicular (ou paralela) a outra.

Problemas resolvidos da inclinação de uma linha

Exercício 1

Encontre a inclinação da reta que passa pelos dois pontos a seguir:

$P_1(5,6) \qquad P_2(8,3)$

veja solução

Para calcular a inclinação da linha, você deve usar a fórmula:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{3-6}{8-5}=\cfrac{-3}{3} = \bm{-1}$

Exercício 2

Calcule a inclinação da reta que passa pelos dois pontos a seguir:

$P_1(-3,1) \qquad P_2(-2,-4)$

veja solução

Para encontrar a inclinação da linha, você deve usar a fórmula:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-4-1}{-2-(-3)}=\cfrac{-5}{-2+3}=\cfrac{-5}{1} = \bm{-5}$

Exercício 3

Qual é a inclinação de cada linha?

$\begin{array}{lll} A) \ y= 2x+3 & \qquad & B) \ y-3=4(x+1) \\[2ex] C) \ 6x+2y-7=0 & \qquad & D) \ \begin{cases}x=3-t \\[2ex] y=1+2t \end{cases} \end{array}$

veja solução

A) A reta é expressa como uma equação implícita, então sua inclinação é 2 (o termo que acompanha a

$x$

B) A reta é definida por sua equação ponto-inclinação, então sua inclinação é 4 (o número antes dos parênteses).

C) A reta está na forma de equação implícita, então sua inclinação é:

$m= - \cfrac{A}{B} = -\cfrac{6}{2} = \bm{-3}$

D) A reta é definida na forma de equações paramétricas, portanto devemos primeiro encontrar seu vetor direção e com ele podemos calcular a inclinação da reta. Assim, os componentes do vetor de direção são os termos que acompanham o coeficiente

$t:$

$\vv{\text{v}} = (-1,2)$

E uma vez que conhecemos o vetor diretor da reta, podemos determinar a inclinação da reta:

$m = \cfrac{\text{v}_2}{\text{v}_1} = \cfrac{2}{-1} = \bm{-2}$

Exercício 4

Determine a inclinação de cada linha representada graficamente:

equação explícita da linha exercício resolvido passo a passo

veja solução

azul à direita

A linha azul aumenta em um Y para cada X, então sua inclinação é igual a 1.

$m=1$

verde direito

A linha verde aumenta três Y para cada X, então sua inclinação é 3 .

$m=3$

Linha Vermelha

A linha vermelha diminui em dois Y para cada X, então sua inclinação é igual a -2 .

$m=-2$

Fórmula para a inclinação de uma linha

Exemplo de cálculo da inclinação de uma linha a partir de dois pontos

Encontrar a inclinação de uma reta a partir de sua equação

Inclinação dada a equação explícita da reta

Inclinação dada a equação ponto-inclinação da reta

Inclinação dada a equação implícita da reta

Inclinação levando em consideração o vetor de direção da linha

inclinação dado um ângulo

Significado da inclinação de uma linha

Posição relativa das linhas

Problemas resolvidos da inclinação de uma linha

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Deixe um comentário Cancelar resposta