Extraia ou remova o fator comum

Nesta página explicamos como obter (ou extrair) o fator comum de um polinômio. Aqui você encontrará os diferentes tipos de fator comum e poderá ver vários exemplos de como isso é conseguido. Além disso, você pode treinar com exercícios resolvidos passo a passo.

Qual é o fator comum?

Em matemática, o fator comum é um fator presente em todos os termos de um polinômio, ou seja, o fator comum consiste em um número ou letra que multiplica cada termo de um polinômio.

Como exemplo, identificaremos qual é o fator comum do seguinte polinômio:

4x+4y

No número 4 é repetido em todos os termos do polinômio:

\color{red} \bm{4} \color{black} x + \color{red} \bm{4} \color{black} y

O fator comum deste polinômio é, portanto, igual a 4.

\displaystyle \text{Factor com\'un} = 4 {\phantom{\frac{1}{2}}

Como obter (ou extrair) o fator comum

Depois de sabermos o significado do fator comum, vamos ver como obter o fator comum de um polinômio.

Quando dois ou mais termos de um polinômio têm um fator comum, o fator comum pode ser tomado (ou extraído) para transformar adições ou subtrações do polinômio em uma multiplicação.

Isso pode parecer um pouco difícil de escrever, então vamos ver como extrair o fator comum de um polinômio com um exemplo:

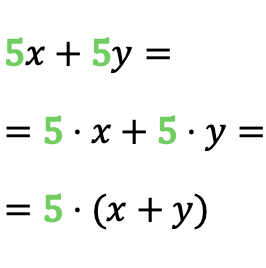
extrair ou remover o fator comum de um polinômio

Como você pode ver no exemplo, o número 5 se repete no monômio 5x e no monômio 5y, então o fator comum do polinômio é 5. Assim, uma vez identificado o fator comum, podemos converter a soma dos monômios em um produtos.

Não esqueça de colocar os parênteses na hora de extrair o fator comum, pois o fator comum deve multiplicar todas as adendas.

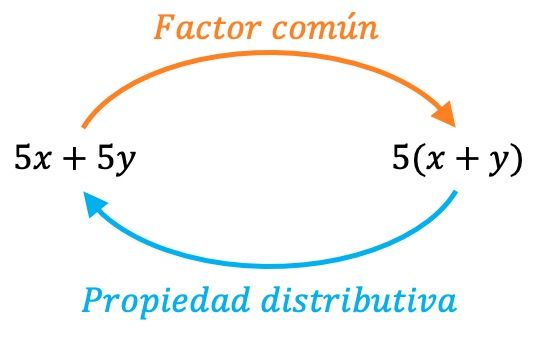
Retirar o fator comum é a operação inversa da propriedade distributiva , ou seja, estamos na verdade aplicando a propriedade distributiva ao contrário. Portanto, podemos sempre verificar se extraímos corretamente o fator comum realizando o processo inverso:

  • Se aplicando a propriedade distributiva obtivemos o mesmo polinômio desde o início, isso significa que obtivemos o fator comum corretamente.
  • Por outro lado, quando o resultado da utilização da propriedade distributiva é outro polinômio diferente do polinômio original, implica que cometemos um erro no processo de extração do fator comum.
fator comum e propriedade distributiva

Exemplos de tomada (ou extração) de fator comum

Deixamos mais exemplos para finalizar a compreensão do conceito de fator comum:

Exemplo 1

Como você pode ver neste exemplo, um fator comum pode ser extraído de mais de dois termos ao mesmo tempo:

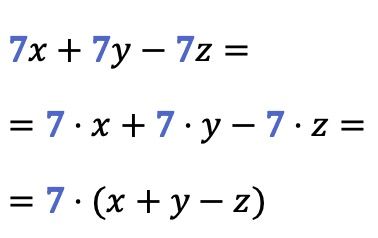
calculadora de fator comum

Exemplo 2

Você também pode extrair um fator comum das variáveis (ou letras):

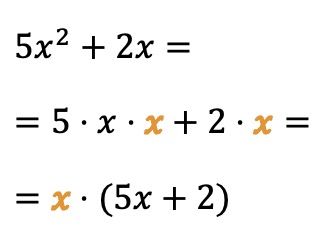
extrair fator comum em expressões algébricas

Neste caso, a letra x multiplica os dois termos do polinômio, então podemos simplificar a expressão algébrica tomando a variável x como fator comum.

Exemplo 3

Neste exemplo, o primeiro termo tem a variável x elevada à potência de 3 e no segundo termo o x é elevado à potência de 2, portanto ambos os termos têm dois x’s. O fator comum não é, portanto, apenas um x, mas x 2 :

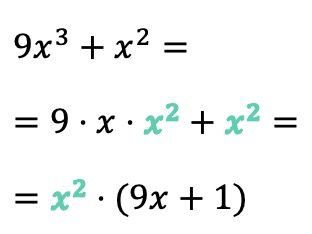
fator comum de álgebra de x ao quadrado

Por outro lado, observe que se o fator comum do polinômio coincide exatamente com um termo, ao extrairmos o fator comum devemos colocar 1 em seu lugar . Caso contrário, se não colocássemos nada no seu lugar, não obteríamos uma expressão equivalente.

como extrair ou encontrar um fator comum

Exemplo 4

Às vezes, o fator comum não é tão óbvio e não é diretamente visível, mas é um divisor dos coeficientes dos monômios. Por exemplo, o fator comum no exemplo a seguir é 3, uma vez que a decomposição fatorial de 6 e 9 contém 3:

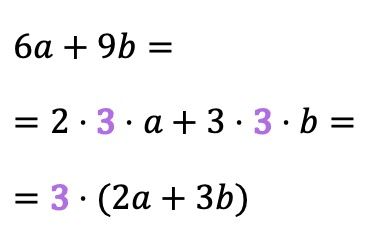
fator comum máximo

Este tipo de fator comum é denominado em alguns livros de álgebra fator comum máximo , pois o fator comum é ao mesmo tempo o máximo fator comum (MDC) dos coeficientes dos termos polinomiais.

Se você chegou até aqui, significa que provavelmente já sabe como encontrar o fator comum de um polinômio, perfeito. Porém, você ainda não se perguntou para que serve o fator comum? Bem, uma aplicação do fator comum é que ele é usado para fatorar polinômios. Se você ainda não sabe o que é, neste link você poderá ver o que é fatoração polinomial e porque o fator comum é tão importante para realizar esta operação polinomial.

Fator comum para frações

O fator comum também é muito útil para simplificar termos em frações com polinômios no numerador e no denominador.

Para ver como isso é feito, vamos simplificar a seguinte fração como exemplo:

\cfrac{2x^2+4}{14x+8y}

A primeira coisa que precisamos fazer é determinar o fator comum do polinômio do numerador e do polinômio do denominador. Neste caso, o fator comum dos dois polinômios é 2:

\cfrac{\color{red} \bm{2} \color{black}\cdot x^2+\color{red} \bm{2} \color{black}\cdot 2 }{\color{red} \bm{2} \color{black}\cdot 7x+\color{red} \bm{2} \color{black} \cdot 4y}

Agora vamos extrair o fator comum dos dois polinômios:

\cfrac{\color{red} \bm{2} \color{black}\left(x^2+2\right)}{\color{red} \bm{2} \color{black}\left(7x+4y\right)}

E uma vez obtido um fator comum para ambos os polinômios, precisamos retirar os fatores que se repetem no numerador e no denominador :

\cfrac{\cancel{2}\left(x^2+2\right)}{ \cancel{2}\left(7x+4y\right)}

Concluindo, a fração simplificada é:

\cfrac{x^2+2}{7x+4y}

Fator comum por agrupamento

Uma maneira de reduzir os termos de um polinômio é usar o método do fator comum agrupando os termos , também chamado de extração de fator comum duplo. Como o próprio nome sugere, este procedimento consiste em simplificar a expressão de um polinômio agrupando seus termos duas vezes.

Este método é um pouco complexo, então vamos ver como ele é aplicado passo a passo com o seguinte polinômio:

x^2+2x+5x+10

Primeiro precisamos determinar dois possíveis fatores comuns diferentes, então separamos o polinômio em duas partes:

(x^2+2x)+(5x+10)

Neste caso, os elementos x 2 e 2x têm a letra x como fator comum, e os termos 5x e 10 têm 5 como fator comum (já que 10 é múltiplo de 5). Portanto, temos esses dois fatores em comum:

(x\cdot x+2\cdot x)+(5\cdot x+5\cdot 2)

x(x+2)+5(x+2)

E finalmente, como os dois produtos polinomiais restantes têm o fator (x+2), podemos simplificar o polinômio da seguinte forma:

(x+2)\cdot (x+5)

Como você pode ver, esse método não é nada fácil. Portanto, não hesite em nos fazer qualquer pergunta nos comentários, e nós responderemos o mais breve possível.

Exercícios de fatores comuns resolvidos passo a passo

Deixamos vários exercícios resolvidos passo a passo para que você possa praticar a extração do fator comum de um polinômio.

Exercício 1

Extraia o fator comum dos seguintes polinômios:

\text{A)} \ 6a+6b

\text{B)} \ 3x^2+8x

\text{C)} \ 2x-4

\text{D)} \ -5x^4+x^2

A) Todos os termos que compõem o primeiro polinômio possuem 6, então o fator comum do polinômio é 6:

6a+6b = 6\cdot a + 6 \cdot b = \bm{6\cdot (a+b)}

B) No segundo polinômio, todos os seus elementos possuem pelo menos uma letra x. Aqui está o fator comum do polinômio:

3x^2+8x = 3x \cdot x+8\cdot x= \bm{x\cdot (3x+8)}

C) O primeiro monômio do polinômio obviamente tem 2, e o segundo monômio é um múltiplo de 2. Portanto, o fator comum do polinômio é 2:

2x-4= 2\cdot x - 2\cdot 2 =\bm{2\cdot (x-2)}

D) No último polinômio todas as variáveis são pelo menos elevadas ao quadrado. O fator comum é, portanto, x 2 :

-5x^4+x^2= -5x^2\cdot x^2 +1 \cdot x^2 = \bm{x^2\cdot (-5x^2+1)}

Lembre-se que quando o fator comum é idêntico a um termo, deve-se colocar 1 em seu lugar.

Exercício 2

Considere o fator comum dos seguintes polinômios:

\text{A)} \ 8x^2 + 10y^3

\text{B)} \ 5x^3-2x^2+4x

\text{C)} \ 25x^5+15x^3-20

\text{D)} \ 9x^4-3x^3-21x^2-6x

A) Todos os coeficientes dos elementos que compõem o primeiro polinômio são múltiplos de 2, portanto, ao extrair o fator comum o polinômio fica:

\begin{array}{l} 8x^2 + 10y^3 = \\[2ex] = 2\cdot 4x^2 +2\cdot 5y^3 = \\[2ex] = \bm{2\left(4x^2+5y^3\right)} \end{array}

B) Em todos os termos do polinômio existe pelo menos um x, portanto:

\begin{array}{l}5x^3-2x^2+4x = \\[2ex] = 5x^2\cdot x-2x\cdot x+4\cdot x= \\[2ex] =\bm{x\left(5x^2-2x+4\right)}\end{array}

C) O máximo divisor comum dos coeficientes de todos os termos do polinômio é 5, de modo que o divisor comum do referido polinômio é 5:

\begin{array}{l}25x^5+15x^3-20 = \\[2ex] =5\cdot 5x^5+5\cdot 3x^3-5\cdot 4 = \\[2ex] = \bm{5\left(5x^5+3x^3-4\right)}\end{array}

D) Todos os termos do polinômio possuem pelo menos um x e, além disso, todos os coeficientes são múltiplos de 3. Portanto, o fator comum do polinômio é 3x:

\begin{array}{l}9x^4-3x^3-21x^2-6x = \\[2ex] = 3x^3\cdot 3x-x^2\cdot 3x-7x\cdot 3x-2\cdot 3x= \\[2ex] = \bm{3x\left(3x^3-x^2-7x-2 \right)}\end{array}

Exercício 3

Encontre o fator comum de cada um dos seguintes polinômios e subtraia-o:

\text{A)} \ 4a^2b^5+7a^4b^3-10a^6b^4

\text{B)} \ 16x^4y^7z+8x^2y^2z^2+ 24x^3y^5

\text{C)} \ 6ab^2c^4-6ab^2c+12a^3b^2c

\text{D)} \ 18x^2y+10xy-5xy^3+4z

A) Todos os monômios têm pelo menos a letra

a

ao quadrado e a letra

b

ao cubo, então o fator comum é

a^2b^3:

\begin{array}{l} 4a^2b^5+7a^4b^3-10a^6b^4 = \\[2ex] = 4b^2\cdot a^2b^3+7a^2\cdot a^2b^3-10a^4b\cdot a^2b^3 = \\[2ex] = \bm{a^2b^3\left(4b^2+7a^2-10a^4b\right)} \end{array}

B) Todos os coeficientes do polinômio são múltiplos de 8 e, além disso, possuem pelo menos x 2 e y 2 como partes literais. O fator comum do polinômio é, portanto, 8x 2 y 2 .

\begin{array}{l}16x^4y^7z+8x^2y^2z^2+ 24x^3y^5 = \\[2ex] = 2x^2y^5z \cdot 8x^2y^2 +z^2\cdot 8x^2y^2+ 3xy^3\cdot 8x^2y^2= \\[2ex] =\bm{8x^2y^2\left(2x^2y^5z+z^2+3xy^3\right)}\end{array}

C) Neste caso, o fator comum coincide com o valor do monômio intermediário

\left(6ab^2c\right)

, uma vez que os coeficientes dos outros monômios são múltiplos de

6

e absolutamente todo mundo tem

ab^2c:

\begin{array}{l}6ab^2c^4-6ab^2c+12a^3b^2c = \\[2ex] =c^3\cdot 6ab^2c -1\cdot 6ab^2c+2a^2 \cdot 6ab^2c = \\[2ex] = \bm{6ab^2c\left(c^3-1+2a^2\right)}\end{array}

D) Neste caso particular, o polinômio não possui fator comum, pois nenhum fator se repete em todos os termos do polinômio. Portanto, a expressão polinomial não pode ser simplificada algebricamente.

18x^2y+10xy-5xy^3+4z

Exercício 4

Simplifique as seguintes frações algébricas tomando o fator comum:

\text{A)} \ \cfrac{10x^2+30}{5x-20}

\text{B)} \ \cfrac{16x^2-8}{24x-32}

\text{C)} \ \cfrac{49x^3+7x}{35x^2-14}

\text{D)} \ \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}

O procedimento para simplificar uma fração algébrica, ou seja, uma fração com polinômios, consiste em extrair o fator comum do numerador e denominador da fração e, em seguida, eliminar os fatores que se repetem acima e abaixo. abaixo da fração. ENTÃO:

\text{A)} \quad \begin{array}{l} \cfrac{10x^2+30}{5x-20}= \cfrac{5\cdot 2x^2 +5\cdot 6}{5\cdot x-5\cdot 4} = \\[4ex] = \cfrac{5(2x^2+6)}{5(x-4)}= \cfrac{\cancel{5}(2x^2+6)}{\cancel{5}(x-4)} = \\[4ex] = \cfrac{\bm{2x^2+6}}{\bm{x-4}} \end{array}

\text{B)} \quad \begin{array}{l} \cfrac{16x^2-8}{24x-32} = \cfrac{8 \cdot 2x^2+8 \cdot (-1)}{8 \cdot 3x-8 \cdot 4} =\\[4ex] = \cfrac{8(2x^2-1)}{8(3x-4)}= \cfrac{\cancel{8}(2x^2-1)}{\cancel{8}(3x-4)} =\\[4ex] = \cfrac{\bm{2x^2-1}}{\bm{3x-4}} \end{array}

\text{C)} \quad \begin{array}{l}\cfrac{49x^3+7x}{35x^2-14}=\cfrac{7x\cdot 7x^2+7x\cdot 1}{7 \cdot 5x^2+7\cdot (-2)} =\\[4ex] = \cfrac{7x(7x^2+1)}{7(5x^2-2)}= \cfrac{\cancel{7}x(7x^2+1)}{\cancel{7}(5x^2-2)}=\\[4ex] = \cfrac{\bm{x(7x^2+1)}}{\bm{5x^2-2}} \end{array}

\text{D)} \quad \begin{array}{l} \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}=\cfrac{4x^2\cdot 2x^2+4x^2\cdot 4x+4x^2\cdot (-1)}{4x\cdot 3x+4x\cdot 5}=\\[4ex] = \cfrac{4x^2(2x^2+4x-1)}{4x(3x+5)}= \cfrac{\cancel{4}x^{\cancel{2}}(2x^2+4x-1)}{\cancel{4}\cancel{x}(3x+5)}=\\[4ex] = \cfrac{\bm{x(2x^2+4x-1)}}{\bm{3x+5}} \end{array}

Exercício 5

Tome o fator comum das seguintes expressões polinomiais:

\text{A)} \ \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}

\text{B)} \ \sqrt{12x^3+16}

\text{C)} \ x^2+4x-3x-12

\text{D)} \ \cfrac{3}{4}x^2+ \cfrac{1}{2}x-\cfrac{5}{6}

A) Todos os termos do polinômio podem ser decompostos fatorialmente ao terceiro, portanto:

\begin{array}{l} \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}= \\[3ex] = \cfrac{1}{3}\cdot 7x^2+ \cfrac{1}{3}\cdot 8x-\cfrac{1}{3}\cdot 2 = \\[3ex] = \mathbf{\cfrac{1}{3}}\bm{\left(7x^2+8x-2\right)} \end{array}

B) O fator comum do polinômio dentro da raiz é 4, mas, então, podemos gerar o fator comum calculando sua raiz quadrada:

\begin{array}{l}\sqrt{12x^3+16}= \\[2ex] =\sqrt{4\cdot 3x^3+4\cdot 4}= \\[2ex]=\sqrt{4\left(3x^3+4\right)}= \\[2ex] =\bm{2\sqrt{3x^3+4}}\end{array}

C) Neste polinômio podemos aplicar o processo de extração do fator comum agrupando:

\begin{array}{l}x^2+4x-3x-12= \\[2ex] =x(x+4)-3(x+4) = \\[2ex] = \bm{(x+4)(x-3)}\end{array}

D) Todos os coeficientes fracionários do polinômio são múltiplos de metade, então o fator comum do polinômio é ½.

\begin{array}{l}\displaystyle \frac{3}{4}x^2+ \frac{1}{2}x-\frac{5}{6}= \\[4ex] \displaystyle = \frac{1}{2}\cdot\frac{3}{2}x^2+ \frac{1}{2}\cdot x-\frac{1}{2}\cdot\frac{5}{3}= \\[4ex] \displaystyle = \mathbf{\frac{1}{2}}\bm{\left(}\mathbf{\frac{3}{2}}\bm{x^2+x-}\mathbf{\frac{5}{3}} \bm{\right)}\end{array}

👇👇👇 O que você achou da explicação? Você gostou? Lembre-se também que se você tiver alguma dúvida sobre como é determinado o fator comum de um polinômio ou se não entender algum exercício, pode sempre nos perguntar nos comentários, e nós responderemos. 👇👇👇

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima