Faixa de uma matriz baseada em um parâmetro -

Nesta página você verá como calcular a classificação de uma tabela com base em um parâmetro. Você também encontrará exemplos passo a passo e exercícios resolvidos sobre como encontrar o contradomínio de uma matriz com base em um parâmetro.

Para compreender totalmente o procedimento de estudo do posto de matrizes com parâmetros, é importante que você já saiba calcular o posto de uma matriz por determinantes . Portanto, recomendamos que você aprenda essas duas coisas antes de continuar lendo.

Como calcular o intervalo de um array com base em um parâmetro. Exemplo:

Determina o intervalo da matriz A com base em diferentes valores de parâmetros
$\displaystyle a :$

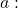
$\displaystyle A= \begin{pmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{pmatrix}$

A matriz A terá no máximo classificação 3, porque é uma matriz de ordem 3. Portanto, a primeira coisa que precisamos fazer é resolver o determinante de toda a matriz 3×3 com a regra de Sarrus , para ver se ele pode ser de posto 3:

$\displaystyle \begin{aligned} \begin{vmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{vmatrix} & =-a(a+1)+0+0+a+1-0-0 \\ & =-a^2-a+a+1 \\[1.5ex] & =-a^2+1 \end{aligned}$

O resultado do determinante é uma função do parâmetro

$\displaystyle a$

. Portanto, definimos o resultado igual a 0 para ver quando a tabela será de classificação 2 e quando será de classificação 3:

$\displaystyle -a^2+1 = 0$

E resolvemos a equação resultante:

$\displaystyle a^2 = 1$

$\displaystyle \sqrt{a^2} = \sqrt{1}$

$\displaystyle \bm{a = \pm 1}$

Portanto, quando

$\displaystyle a$

seja +1 ou -1, o determinante 3×3 será 0 e, portanto, o posto da matriz não será 3. Por outro lado, quando

$\displaystyle a$

for diferente de +1 e -1, o determinante será diferente de 0 e, portanto, a matriz terá posto 3.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq +1,-1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

Agora vamos ver o que acontece quando

$\displaystyle \bm{a=+1} :$

$\displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & -1 & 2 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & 1 \end{pmatrix}$

Como vimos anteriormente, quando

$\displaystyle a$

é 1, o determinante da matriz é 0. Portanto, não pode ser de posto 3. Tentamos agora calcular um determinante 2×2 diferente de 0 dentro da matriz, por exemplo, o do canto superior esquerdo:

$\displaystyle \begin{vmatrix} 2 & -1 \\[1.1ex] 0 & -1 \end{vmatrix} =-2-0= -2 \neq 0$

O determinante de ordem 2 é diferente de 0. Assim, quando o parâmetro

$\displaystyle a$

ou +1, a classificação da matriz será 2:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Uma vez que vemos o contradomínio da matriz quando

$\displaystyle a \neq +1,-1$

e quando

$\displaystyle a=+1$

Vamos ver o que acontece quando

$\displaystyle \bm{a = -1} :$

$\displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 0 & -1 & 0 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & -1 \end{pmatrix}$

Como vimos no início, quando

$\displaystyle a$

es -1 e o determinante da matriz é 0. Portanto, ela não pode ser definida como classificação 3. Portanto, devemos tentar encontrar um determinante de 2×2 na matriz que seja diferente de 0, por exemplo, o menor parte da matriz. ESQUERDA:

$\displaystyle \begin{vmatrix} 0 & -1 \\[1.1ex] 1 & -2 \end{vmatrix} = 0-(-1)= 1\neq 0$

O determinante da dimensão 2 é diferente de 0. Assim, quando o parâmetro

$\displaystyle a$

ou -1, a classificação da tabela será 2:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Encontramos, portanto, 3 casos diferentes em que a classificação da matriz A depende do valor que o parâmetro assume

$\displaystyle a.$

Aqui está o resumo :

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

Agora que você sabe como discutir o intervalo de matrizes dependentes de parâmetros, pode praticar os exercícios passo a passo abaixo. Para resolvê-los, as propriedades dos determinantes certamente irão ajudá-lo, então se você não tem muita clareza sobre eles, aconselho primeiro a dar uma olhada na página do link, onde cada um deles é explicado com exemplos.

Corrigidos problemas de intervalo de matriz baseado em parâmetros

Exercício 1

Estude o intervalo da tabela a seguir com base no valor do parâmetro

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}$

veja solução

A matriz A terá no máximo classificação 3, porque é uma matriz 3×3. Portanto, a primeira coisa que precisamos fazer é resolver o determinante de toda a matriz (com a regra de Sarrus), para ver se ela pode ser de posto 3:

$\displaystyle \begin{vmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix} =0-8+2a-4a+12-0 =-2a+4$

Definimos o resultado igual a 0 para ver quando o array terá a classificação 2 e quando a classificação 3:

$\displaystyle -2a+4=0$

$\displaystyle -2a=-4$

$\displaystyle a=\cfrac{-4}{-2} = 2$

Portanto, quando

$\displaystyle a$

for diferente de 2, o determinante 3×3 será diferente de 0 e, portanto, o posto da matriz será 3.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq 2 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

Agora vamos ver o que acontece quando

$\displaystyle a=2 :$

$\displaystyle a = 2 \longrightarrow A= \begin{pmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 3 & 1 \\[1.1ex] 2 & 2 \end{vmatrix} = 6-2 = 4 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = 2 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Encontramos portanto 2 casos em que a imagem da matriz A varia com o valor que o parâmetro assume:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 2 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 2\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

Exercício 2

Encontre o intervalo da tabela a seguir com base no valor do parâmetro

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{pmatrix}$

veja solução

$\displaystyle \begin{aligned} \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{vmatrix} & =2a-12-2a+2+12-2a^2 \\ &=2-2a^2\end{aligned}$

Definimos o resultado igual a 0 para ver quando o array terá a classificação 2 e quando a classificação 3:

$\displaystyle 2-2a^2=0$

$\displaystyle -2a^2=-2$

$\displaystyle a^2=\cfrac{-2}{-2}$

$\displaystyle a^2=1$

$\displaystyle a=\pm 1$

Portanto, quando

$\displaystyle a$

for diferente de +1 e -1, o determinante 3×3 será diferente de 0 e, portanto, o posto da matriz será 3.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq +1, -1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

Agora vamos ver o que acontece quando

$\displaystyle a=+1 :$

$\displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 1 & 3 \end{vmatrix} = 6-1 = 5 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Agora vamos ver o que acontece quando

$\displaystyle a=-1 :$

$\displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 2 & 2 \\[1.1ex] -1 & 1 \end{vmatrix} =2-(-2) = 4 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Encontramos, portanto, 3 casos em que o intervalo da matriz A varia dependendo do valor que o parâmetro assume:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

Exercício 3

Calcula o intervalo da tabela a seguir com base no valor do parâmetro

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{pmatrix}$

veja solução

$\displaystyle \begin{aligned} \begin{vmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{vmatrix} & =(a+1)(a-3) +2+0-5+6(a+1)-0 \\ & = a^2-3a+a-3 +2-5+6a+6 \\[1.5ex] & =a^2+4a\end{aligned}$

Definimos o resultado igual a 0 para ver quando o array terá a classificação 2 e quando a classificação 3:

$\displaystyle a^2+4a=0$

Esta é uma equação quadrática incompleta, então extraímos um fator comum:

$\displaystyle a(a+4)=0$

E definimos cada termo igual a 0:

$\displaystyle a(a+4)=0 \longrightarrow \begin{cases} \bm{a = 0} \\[2ex] a+4=0 \ \longrightarrow \ \bm{a=-4}\end{cases}$

Obtivemos 0 e -4 como soluções. Portanto, quando

$\displaystyle a$

for diferente de 0 e -4, o determinante 3×3 será diferente de 0 e, portanto, o posto da matriz será 3.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq 0, -4 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

Agora vamos ver o que acontece quando

$\displaystyle a=0 :$

$\displaystyle a = 0 \longrightarrow A= \begin{pmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 1 & 1 \\[1.1ex] 0 & 1 \end{vmatrix} = 1-0 = 1 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = 0 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Agora vamos ver o que acontece quando

$\displaystyle a=-4 :$

$\displaystyle a = -4 \longrightarrow A= \begin{pmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} -3 & 1 \\[1.1ex] 0 & 1\end{vmatrix} =-3-0 = -3 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -4 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Encontramos, portanto, 3 casos em que o intervalo da matriz A varia dependendo do valor que o parâmetro assume:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 0,-4 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 0\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -4\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

Exercício 4

Encontre a extensão da seguinte matriz de dimensão 3×4 de acordo com o valor do parâmetro

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&a \end{pmatrix}$

veja solução

A matriz A terá no máximo posto 3, pois não podemos calcular nenhum determinante 4×4 . Portanto, a primeira coisa que precisamos fazer é resolver todos os possíveis determinantes de ordem 3 (com a regra de Sarrus), para ver se podem ser de ordem 3:

$\displaystyle \begin{aligned} \begin{vmatrix} -1&-3&-2\\[1.1ex] 4&12&8\\[1.1ex] 2&6&4 \end{vmatrix} & =-48-48-48+48+48+48 =\bm{0}\end{aligned}$

$\displaystyle \begin{aligned} \begin{vmatrix} -1&-3&1\\[1.1ex] 4&12&-4\\[1.1ex] 2&6&a \end{vmatrix} & =-12a+24+24-24-24+12a=\bm{0}\end{aligned}$

$\displaystyle \begin{aligned} \begin{vmatrix} -1&-2&1\\[1.1ex] 4&8&-4\\[1.1ex] 2&4&a \end{vmatrix} & =-8a+16+16-16-16+8a=\bm{0}\end{aligned}$

$\displaystyle \begin{aligned} \begin{vmatrix} -3&-2&1\\[1.1ex] 12&8&-4\\[1.1ex] 6&4&a \end{vmatrix} & =-24a+48+48-48-48+24a=\bm{0}\end{aligned}$

Os resultados de todos os determinantes possíveis de ordem 3 são 0, qualquer que seja o valor de

$\displaystyle a$

. Assim, a matriz nunca será de posto 3, pois não importa o valor que ela assuma

$\displaystyle a$

que nunca haverá um determinante 3×3 diferente de 0.

Então agora tentamos determinantes de dimensão 2 × 2. No entanto, todos os determinantes de ordem 2 também dão 0, exceto os seguintes:

$\displaystyle \begin{aligned} \begin{vmatrix} 8&-4\\[1.1ex] 4&a \end{vmatrix} & =8a+16 \end{aligned}$

Agora definimos o resultado igual a 0 e resolvemos a equação:

$\displaystyle 8a+16=0$

$\displaystyle 8a=-16$

$\displaystyle a=\cfrac{-16}{8} =-2$

Portanto, quando

$\displaystyle a$

for diferente de -2, o determinante 2×2 será diferente de 0 e, portanto, o posto da matriz será 2.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq -2 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Agora vamos ver o que acontece quando

$\displaystyle a=-2 :$

$\displaystyle a = -2 \longrightarrow A= \begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&-2 \end{pmatrix}$

Como vimos anteriormente, quando

$\displaystyle a$

é -2, todos os determinantes de ordem 2 são 0. Não pode, portanto, ser de posto 2. E como existe pelo menos um determinante 1×1 diferente de 0, neste caso o posto da matriz é 1:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -2 \ \longrightarrow \ Rg(A)=1} \phantom{33} \\[-2ex] & \end{array} }$

Encontramos portanto 2 casos em que a imagem da matriz A varia com o valor que o parâmetro assume:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq -2 \longrightarrow \ Rg(A)=2} \phantom{33} \\[3ex] \color{black} \bm{a = -2\ \longrightarrow \ Rg(A)=1} \\ & \end{array} }$

Intervalo de um array baseado em um parâmetro

Como calcular o intervalo de um array com base em um parâmetro. Exemplo:

Corrigidos problemas de intervalo de matriz baseado em parâmetros

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Deixe um comentário Cancelar resposta