Matriz simétrica - Matoridade

Nesta página você encontrará a explicação do que são matrizes simétricas. Além disso, mostramos como identificar rapidamente quando uma matriz é simétrica, junto com diversos exemplos para que você não tenha dúvidas. Você também encontrará todas as propriedades das matrizes simétricas. E por fim, explicamos uma característica particular que qualquer matriz quadrada possui: ela pode ser decomposta na soma de uma matriz simétrica e de uma matriz antissimétrica.

O que é uma matriz simétrica?

A definição de uma matriz simétrica é a seguinte:

Uma matriz simétrica é uma matriz quadrada cuja transposta é igual à própria matriz.

$A^t = A$

Ouro

$A^t$

representa a matriz transposta de

$A$

Depois de conhecermos o conceito de matriz simétrica, veremos como qualquer matriz simétrica pode ser facilmente identificada:

Quando uma matriz é simétrica?

Reconhecer a estrutura de uma matriz simétrica é muito simples: o elemento da linha i e da coluna j deve ser idêntico ao elemento da linha j e da coluna i . E os valores da diagonal principal da matriz podem ser quaisquer.

Exemplos de matrizes simétricas

Aqui estão vários exemplos de matrizes simétricas para ajudá-lo a entender:

Exemplo de uma matriz simétrica de ordem 2 × 2

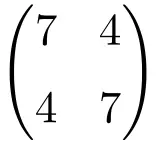
exemplo de uma matriz simétrica de dimensão 2x2

Exemplo de uma matriz simétrica de dimensão 3×3

exemplo de uma matriz simétrica de dimensão 3x3

Exemplo de uma matriz simétrica de tamanho 4×4

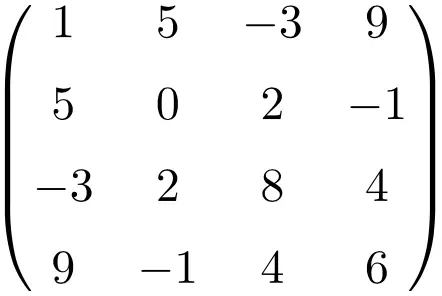
exemplo de uma matriz simétrica de dimensão 4x4

Ao transpor estas três matrizes verificamos que elas são simétricas, pois as matrizes transpostas são equivalentes às suas respectivas matrizes originais.

Por que é chamada de matriz simétrica?

Se você observar atentamente os exemplos anteriores, a diagonal principal de uma matriz simétrica é um eixo de simetria, ou em outras palavras, atua como um espelho entre os números acima da diagonal e os abaixo. Por esse motivo, esses tipos de matrizes são chamados de simétricas.

Propriedades de matrizes simétricas

As características das matrizes simétricas são as seguintes:

Adicionar (ou subtrair) duas matrizes simétricas resulta em outra matriz simétrica. Visto que transpor duas matrizes adicionadas (ou subtraídas) é equivalente a transpor cada matriz separadamente:

$\displaystyle \left(A+B\right)^t = A^t+B^t = A+B$

Qualquer matriz simétrica multiplicada por um escalar também dá origem a outra matriz simétrica.

Da mesma forma, o produto matricial entre duas matrizes simétricas nem sempre é igual a outra matriz simétrica, apenas se e somente se as duas matrizes puderem ser comutadas. Esta condição pode ser provada com a propriedade de multiplicação de matrizes transpostas:

$\displaystyle \left(A\cdot B\right)^t = B^t\cdot A^t = BA=AB$

A potência de uma matriz simétrica dá origem a outra matriz simétrica, desde que o expoente seja um número inteiro.

Obviamente, a matriz unitária e a matriz zero são exemplos de matrizes simétricas.

Uma matriz congruente com uma matriz simétrica também deve ser simétrica.

Se uma matriz simétrica for regular ou invertível, então sua matriz inversa também será simétrica.

O mesmo acontece com a matriz adjunta de uma matriz simétrica: a matriz adjunta de uma matriz simétrica fornece outra matriz simétrica como solução.

Uma matriz verdadeiramente simétrica também é uma matriz normal.

Como as matrizes simétricas são um caso especial de matrizes Hermitianas, todos os autovalores (ou autovalores) de uma matriz simétrica são números reais.

O teorema espectral nos diz que todas as matrizes cujos elementos são reais são matrizes diagonalizáveis e, além disso, a diagonalização é realizada por meio de uma matriz ortogonal. Portanto, todas as matrizes simétricas reais são diagonalizadas ortogonalmente.

Por outro lado, matrizes simétricas com números complexos podem ser diagonalizadas através de uma matriz unitária.

A matriz Hessiana é sempre simétrica.

Decomposição de uma matriz quadrada em uma matriz simétrica e uma matriz antissimétrica

Uma característica especial das matrizes quadradas é que elas podem ser decompostas na soma de uma matriz simétrica mais uma matriz antissimétrica.

A fórmula que nos permite fazer isso é a seguinte:

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

Onde C é a matriz quadrada que queremos decompor, C ^t sua transposta e, finalmente, S e A são respectivamente as matrizes simétricas e antissimétricas nas quais a matriz C é decomposta.

Abaixo você tem um exercício resolvido para ver como isso é feito. Vamos decompor a seguinte matriz:

$\displaystyle C=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

Calculamos a matriz simétrica e antissimétrica com as fórmulas:

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}$

E podemos verificar se a equação é cumprida somando as duas matrizes:

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}+\begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

$\displaystyle C=S+A$

✅