Matrizes semelhantes ou semelhantes

Nesta página você encontrará a explicação de matrizes semelhantes, também chamadas de matrizes semelhantes. Além disso, mostramos um exemplo claro de duas matrizes semelhantes e todas as propriedades deste tipo de matrizes para que você não tenha dúvidas. Finalmente, você poderá até ver como elas se relacionam com matrizes congruentes.

O que são matrizes semelhantes (ou semelhantes)?

A definição de matrizes semelhantes é a seguinte:

duas matrizes

$A$

$B$

são semelhantes (ou semelhantes) se existir uma matriz

$P$

com o qual a seguinte condição é atendida:

$P^{-1}AP = B$

Ou equivalente:

$AP = PB$

Na verdade, a matriz

$P$

atua como uma matriz de mudança básica. Portanto, o que esta equação significa é que a matriz

$A$

pode ser expresso em outra base (

$P$

), o que dá origem à matriz

$B$

Este termo também pode ser chamado de transformação de similaridade , já que na verdade estamos transformando a matriz

$A$

na matriz

$B$

Obviamente a matriz

$P$

deve ser uma matriz regular ou não degenerada (determinante diferente de zero).

Por outro lado, podemos indicar que duas matrizes são semelhantes à seguinte expressão:

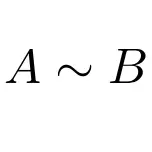
explicação de matrizes semelhantes ou semelhantes

Esta classe de matrizes é mais importante do que parece para a álgebra linear. Eles são usados principalmente para matrizes diagonalizáveis, pois o procedimento para diagonalizar qualquer matriz é baseado no conceito de similaridade de matrizes.

Na verdade, o processo de diagonalização de uma matriz envolve o cálculo de uma matriz semelhante que, ao mesmo tempo, é uma matriz diagonal. Você pode ver como isso é feito em como diagonalizar uma matriz .

Exemplo de matrizes semelhantes ou semelhantes

A seguir veremos um exemplo de matrizes semelhantes de dimensão 2×2 para finalizar a assimilação do conceito.

As matrizes quadradas A e B são semelhantes entre si através da matriz invertível P:

$\displaystyle A= \begin{pmatrix}-1&2\\[1.1ex] 3&1\end{pmatrix} \qquad B= \begin{pmatrix}-5&-3\\[1.1ex] 6&5\end{pmatrix}$

$\displaystyle P= \begin{pmatrix}2&1\\[1.1ex] -1&0\end{pmatrix}$

Para mostrar que estas matrizes são mutuamente semelhantes, devemos primeiro calcular a matriz inversa de P:

$\displaystyle P^{-1}= \begin{pmatrix}0&-1\\[1.1ex] 1&2\end{pmatrix}$

E agora verificamos se elas são semelhantes realizando o produto matricial que define a similaridade de duas matrizes:

$\displaystyle P^{-1}AP = B \quad ?$

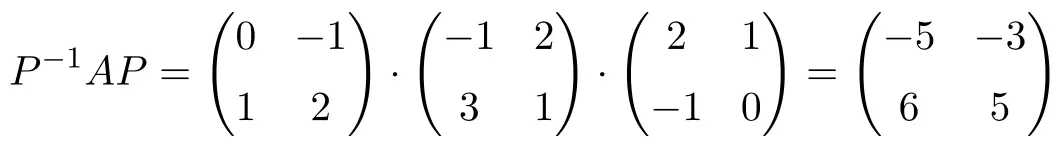
exemplos de matrizes 2x2 semelhantes ou semelhantes

$\displaystyle P^{-1}AP = B$

✅

Sim, a relação de similaridade é cumprida, portanto são matrizes semelhantes.

Propriedades de matriz semelhantes

Duas matrizes semelhantes A e B compartilham as seguintes características:

Mesma classificação.

$rg(A)=rg(B)$

Os determinantes das duas matrizes são iguais.

$det(A)=det(B)$

Mesmo rastreamento.

$tr(A)=tr(B)$

Mesmos autovalores (ou autovalores). No entanto, os autovetores (ou autovetores) geralmente são diferentes.

Mesmo polinômio característico e polinômio mínimo.

A transposição de uma matriz é semelhante à matriz original.

A matriz B pode ser encontrada aplicando operações elementares nas linhas da matriz A e vice-versa.

Obviamente, a semelhança é refletida. Ou seja, se A é semelhante a B, então B também é semelhante a A.

Além disso, a similaridade das matrizes também é simétrica. Ou seja, se com a matriz P pode ser obtida a matriz semelhante a A (B), a matriz semelhante a B (A) também pode ser obtida com a mesma matriz P:

$B=P^{-1}AP$

$A=PBP^{-1}$

Além disso, a semelhança é transitiva. Portanto, se a matriz A é semelhante à matriz B e a matriz B é semelhante à matriz C, a matriz A também é semelhante à matriz C.

$\left. \begin{array}{l}A\sim B \\[2ex] B \sim C \end{array}\right\} \longrightarrow A \sim C$

Finalmente, cada matriz é semelhante a uma matriz dente de serra. E desta propriedade podemos deduzir o seguinte corolário: toda matriz quadrada é semelhante a uma matriz triangular.

matrizes congruentes

Por outro lado, existe também outra relação muito semelhante entre matrizes mas em vez de ser com a matriz inversa, é com a matriz transposta. Isso é chamado de congruência .

Duas matrizes A e B são congruentes se existe uma matriz invertível P com a qual a seguinte igualdade é satisfeita:

$P^tAP = B$

Como você pode ver, este é o análogo de matrizes semelhantes, mas com a matriz transposta.

O que são matrizes semelhantes (ou semelhantes)?

Exemplo de matrizes semelhantes ou semelhantes

Propriedades de matriz semelhantes

matrizes congruentes

Deixe um comentário Cancelar resposta