Matriz antisimétrica

Nesta página explicamos o que são matrizes antissimétricas. Além disso, você poderá ver vários exemplos, bem como sua estrutura típica para entendê-lo perfeitamente. Explicamos também a particularidade de calcular o determinante de uma matriz antissimétrica e todas as propriedades deste tipo de matriz. E, finalmente, você descobrirá como decompor qualquer matriz quadrada na soma de uma matriz simétrica mais outra matriz antissimétrica.

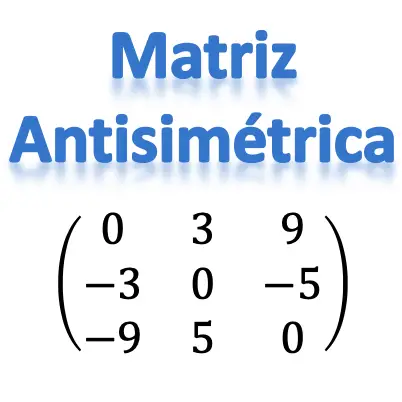
O que é uma matriz antissimétrica?

A definição de matriz antissimétrica é a seguinte:

Uma matriz antissimétrica é uma matriz quadrada cuja transposta é igual ao negativo da matriz.

$A^t = -A$

Ouro

$A^t$

representa a matriz transposta de

$A$

$-A$

é a matriz

$A$

com todos os seus elementos alterados de sinal.

Exemplos de matrizes antissimétricas

Assim que conhecermos o conceito de matriz antissimétrica, veremos vários exemplos de matrizes antissimétricas para melhor entendê-la:

Exemplo de uma matriz antissimétrica de ordem 2 × 2

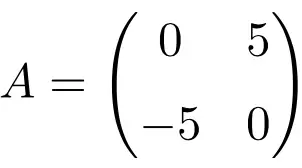
exemplo de matriz antissimétrica de dimensão 2x2

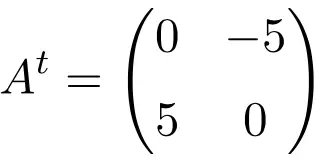
exercício resolvido de matriz antissimétrica de dimensão 2x2

Exemplo de uma matriz antissimétrica de dimensão 3×3

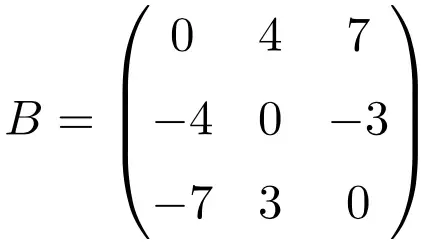
exemplo de matriz antissimétrica de dimensão 3x3

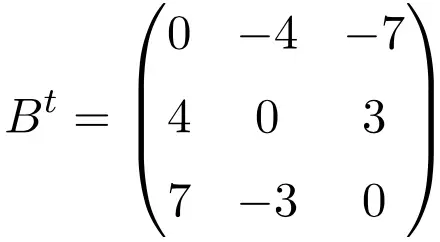
exercício resolvido de matriz antissimétrica de dimensão 3x3

Exemplo de uma matriz antissimétrica de tamanho 4×4

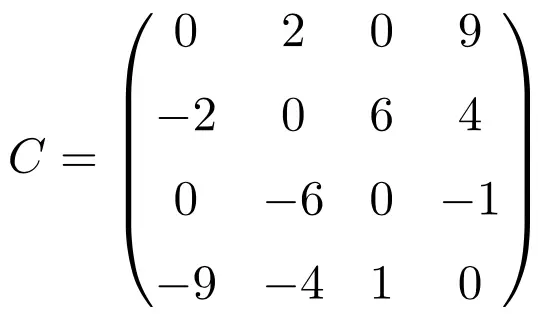
exemplo de matriz antissimétrica de dimensão 4x4

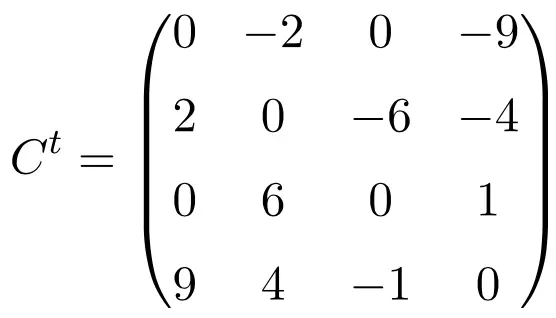
exercício resolvido de matriz antissimétrica de dimensão 4x4

Ao transpor essas três matrizes, verificamos que elas são antissimétricas, pois as matrizes transpostas são equivalentes às suas respectivas matrizes originais de sinal alterado.

Estrutura de uma matriz antissimétrica

Para que a condição da matriz antissimétrica seja atendida, elas devem ter sempre o mesmo tipo de estrutura: os números da diagonal principal são todos iguais a zero e o elemento da linha i e da coluna j é o negativo do elemento da linha j e da coluna eu . Em outras palavras, a forma das matrizes antissimétricas é a seguinte:

$\displaystyle \begin{pmatrix} 0 & a & b & \cdots & c\\[1.1ex]-a & 0 & d & \cdots &e\\[1.1ex]-b & -d & 0 & \cdots & f\\[1.1ex]\vdots & \vdots & \vdots & \ddots & \vdots\\[1.1ex] -c & -e & -f & \cdots & 0\end{pmatrix}$

Portanto, a diagonal principal de uma matriz antissimétrica atua como eixo de antissimetria. É daí que vem o nome desta matriz específica.

Determinante de uma matriz antissimétrica

O determinante de uma matriz antissimétrica depende da dimensão da referida matriz. Isso se deve às propriedades dos determinantes:

$\displaystyle \text{det}(A)=\text{det}(A^t)=\text{det}(-A)=(-1)^n \text{det}(A)$

Assim, se a matriz antissimétrica for de ordem ímpar, seu determinante será igual a 0 . Por outro lado, se a matriz antissimétrica tiver dimensão par, o determinante pode assumir qualquer valor.

Portanto, uma matriz antissimétrica de dimensão ímpar é uma matriz singular ou degenerada. Por outro lado, uma matriz antissimétrica de ordem par é uma matriz regular.

Propriedades de matrizes antissimétricas

As características das matrizes antissimétricas são as seguintes:

Adicionar (ou subtrair) duas matrizes antissimétricas resulta em outra matriz antissimétrica. Visto que transpor duas matrizes adicionadas (ou subtraídas) é equivalente a transpor cada matriz separadamente:

$\displaystyle \left(A+B\right)^t = A^t+B^t = -A-B$

Qualquer matriz antissimétrica multiplicada por um escalar também dá origem a outra matriz antissimétrica.

O poder de uma matriz antissimétrica é equivalente a uma matriz antissimétrica ou a uma matriz simétrica. Se o expoente for um número par, o resultado da potência será uma matriz simétrica, mas se o expoente for um número ímpar, o resultado da potência será uma matriz antissimétrica. Você pode consultar neste link o que é uma matriz simétrica .

O traço de uma matriz antissimétrica é sempre igual a zero.

A soma de qualquer matriz antissimétrica mais a matriz unitária dá origem a uma matriz invertível.

$\displaystyle \text{det}(A+I)\neq 0$

Todos os autovalores reais (ou autovalores) de uma matriz antissimétrica são 0. No entanto, uma matriz antissimétrica também pode ter autovalores complexos.

Todas as matrizes antissimétricas são matrizes normais. Portanto, estão sujeitos ao teorema espectral, que diz que uma matriz antissimétrica pode ser diagonalizada por uma matriz unitária.

Decomposição de uma matriz quadrada em uma matriz simétrica e uma matriz antissimétrica

Uma característica especial das matrizes quadradas é que elas podem ser decompostas na soma de uma matriz simétrica mais uma matriz antissimétrica.

A fórmula que nos permite fazer isso é a seguinte:

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

Onde C é a matriz quadrada que queremos decompor, C ^t sua transposta e finalmente S e A são respectivamente as matrizes simétrica e antissimétrica nas quais a matriz C é decomposta.

Abaixo você tem um exercício resolvido para demonstrar a fórmula. Vamos decompor a seguinte matriz:

$\displaystyle C=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

Calculamos a matriz simétrica e antissimétrica com as fórmulas:

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}$

E podemos verificar se a equação é cumprida somando as duas matrizes:

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}+\begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

$\displaystyle C=S+A$

✅