▷ Teorema do resto: o que é, exemplos e exercícios resolvidos ✅

Aqui você encontrará a explicação do que é o teorema do resto (ou teorema do resto) e como ele é aplicado aos polinômios. Você também poderá ver exemplos e, além disso, praticar com exercícios resolvidos passo a passo sobre o teorema do resto.

Qual é o teorema do resto?

Em matemática, o teorema do resto diz que o resto da divisão de qualquer polinômio P(x) por outro polinômio da forma (xa) é igual ao valor numérico do polinômio P(x) para o valor x=a, Em em outras palavras, o resto da divisão P(x):(xa) é equivalente a P(a).

Exemplo do teorema do resto

Depois de vermos o que é o teorema do resto, vejamos um exemplo prático de sua aplicação:

Calcule o restante da divisão entre os dois polinômios a seguir:

$P(x) = x^3+2x^2-4x+3 \qquad \qquad Q(x)=x-1$

$\cfrac{P(x)}{Q(x)}$

Para encontrar o resto (ou resíduo) da divisão polinomial podemos aproveitar o teorema do resto, pois neste caso o polinômio divisor é da forma (xa), ou seja, é de primeiro grau, o coeficiente de a variável x é 1 e tem um termo independente.

Então aplicamos o teorema do resto, que diz que o resto de uma divisão como esta é igual ao valor numérico do polinômio do dividendo avaliado no termo independente do polinômio divisor com sinal alterado, ou seja, P(1).

Portanto, para encontrar o resto da divisão, precisamos avaliar o polinômio em x=1:

$\begin{aligned} P(1) &= 1^3+2\cdot 1^2-4\cdot 1+3\\[2ex] &= 1+2\cdot 1-4 \cdot 1+3 \\[2ex] & = 1+2-4+3 \\[2ex] & =\bm{2} \end{aligned}$

O restante da divisão entre os polinômios é, portanto, 2 .

Por outro lado, também podemos verificar com a regra de Ruffini para divisão de polinômios que o resto coincide com o resultado que encontramos:

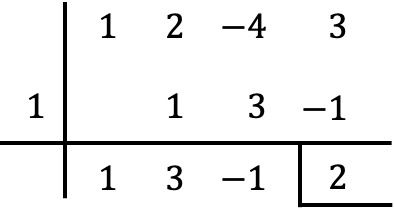
Como você pode ver, é muito mais rápido e fácil determinar o resto de uma divisão de um polinômio por um binômio com o teorema do resto do que com a regra de Ruffini, porque são realizados muito menos cálculos.

Teorema do resto e do fator

Do teorema do resto e da definição da raiz (ou zero) de um polinômio podemos deduzir o teorema do fator. Portanto, o teorema do fator implica o seguinte:

O teorema do fator diz que um polinômio P(x) é divisível por outro polinômio da forma (xa) se, e somente se, P(a)=0. E, neste caso, isso significa que a é uma raiz ou zero do polinômio P(x).

Além disso, de acordo com o teorema do resto, isto significa que se um polinómio é divisível por outro polinómio, o resto da referida divisão é zero, uma vez que P(a)=0.

Por exemplo, se tivermos um certo polinômio:

$P(x)=x^2+2x-8$

Este polinômio é divisível pelo binômio (x-2) porque P(2)=0:

$\begin{aligned} P(2) &= 2^2+2\cdot 2-8\\[2ex] &= 4+4-8 \\[2ex] & =\bm{0} \end{aligned}$

Como x=2 cancela o polinômio P(x), isso significa que x=2 é uma raiz do referido polinômio.

E além disso, como P(2)=0, podemos saber graças ao teorema do resto que o resto da divisão

$\cfrac{x^2+2x-8}{x-2}$

é igual a 0.

Exercícios resolvidos do teorema do resto

Para finalizar a compreensão do teorema do resto, preparamos alguns exercícios resolvidos passo a passo para que você possa praticar. Aconselhamos que você experimente primeiro o exercício e depois verifique se o fez corretamente.

Exercício 1

Encontre, pelo teorema do resto, o resto da divisão polinomial

$\cfrac{P(x)}{Q(x)}$

, sendo os polinômios envolvidos na operação:

$P(x) =x^3+4x^2-2x+1\qquad \qquad Q(x)=x-2$

Veja a solução

O polinômio divisor é composto apenas por um termo de primeiro grau e um termo independente e, além disso, o coeficiente do termo de primeiro grau é 1. Podemos, portanto, utilizar o teorema do resto.

E para aplicar o teorema do resto, basta avaliar o polinômio do dividendo no termo independente do polinômio divisor com sinal alterado, ou seja, devemos calcular P(2).

$\begin{aligned} P(2) &= 2^3+4\cdot 2^2-2\cdot 2+1\\[2ex] &=8+4\cdot 4-2\cdot 2+1 \\[2ex] & = 8+16-4+1 \\[2ex] & =\bm{21} \end{aligned}$

O restante da divisão entre os dois polinômios é, portanto, 21 .

Exercício 2

Dado o polinômio

$P(x)=x^4-2x^3+5x^2-3x+4 ,$

Encontre o resto obtido dividindo-o por cada um dos seguintes polinômios:

$\text{A)} \ \left(x-1 \right)$
$\text{B)} \ \left(x+1 \right)$
$\text{C)} \ \left(x+2 \right)$
$\text{D)} \ \left(x-3 \right)$

Veja a solução

Como todos os polinômios divisórios satisfazem as condições do teorema do resto, podemos usar este teorema para determinar o resto de cada divisão:

$\begin{aligned} \mathbf{A}\bm{)} \ P(1) &= 1^4-2\cdot 1^3+5\cdot 1^2-3\cdot 1+4\\[2ex] &=1-2\cdot 1+5\cdot 1 -3 \cdot 1+4 \\[2ex] & = 1-2+5-3+4 \\[2ex] & =\bm{5} \end{aligned}$

$\begin{aligned} \mathbf{B}\bm{)} \ P(-1) &= (-1)^4-2\cdot (-1)^3+5\cdot (-1)^2-3\cdot (-1)+4\\[2ex] &=1-2\cdot (-1)+5\cdot 1 -3 \cdot (-1)+4 \\[2ex] & = 1+2+5+3+4 \\[2ex] & =\bm{15} \end{aligned}$

$\begin{aligned} \mathbf{C}\bm{)} \ P(-2) &= (-2)^4-2\cdot (-2)^3+5\cdot (-2)^2-3\cdot (-2)+4\\[2ex] &=16-2\cdot (-8)+5\cdot 4 -3 \cdot (-2)+4 \\[2ex] & = 16+16+20+6+4 \\[2ex] & =\bm{62} \end{aligned}$

$\begin{aligned} \mathbf{D}\bm{)} \ P(3) &= 3^4-2\cdot 3^3+5\cdot 3^2-3\cdot 3+4\\[2ex] &=81-2\cdot 27+5\cdot 9 -3 \cdot 3+4 \\[2ex] & = 81-54+45-9+4 \\[2ex] & =\bm{67} \end{aligned}$

Exercício 3

Calcule quanto o parâmetro deve valer

$m$

de modo que o resto da divisão dos polinômios

$\cfrac{P(x)}{Q(x)}$

ser igual a 3, sendo ambos polinômios:

$P(x) =x^3-5x^2-mx+9 \qquad \qquad Q(x)=x+3$

Veja a solução

Neste caso particular, o polinômio divisor é composto por um monômio de primeiro grau e um termo independente e, além disso, o coeficiente do monômio de primeiro grau é 1. Podemos, portanto, utilizar o teorema do resto.

E para usar o teorema do resto, basta substituir o termo independente do polinômio divisor por uma mudança de sinal onde no polinômio dividido há um x, devemos portanto resolver P(-3).

$\begin{aligned} P(-3) &=(-3)^3-5\cdot (-3)^2-m\cdot (-3)+9\\[2ex] &=-27-5\cdot 9 -m\cdot (-3)+9 \\[2ex] & = -27-45+3m+9 \\[2ex] & =3m-63 \end{aligned}$

Mas obviamente obtemos um resultado baseado na incógnita

$m.$

No entanto, a definição do problema nos diz que o resto deve ser igual a três, então devemos definir o resto igual a 3:

$3m-63 = 3$

E finalmente, resolvemos a equação:

$3m = 3+63$

$3m = 66$

$m = \cfrac{66}{3}$

$\bm{m = 22}$

Exercício 4

Determine com o teorema do fator e do resto se o polinômio

$P(x)$

é divisível pelo polinômio

$Q(x).$

$P(x) =-2x^3-5x^2-x+2 \qquad \qquad Q(x)=x+2$

Veja a solução

Para que o polinômio

$P(x)$

ser divisível pelo polinômio

$Q(x)$

a divisão entre esses dois polinômios deve ser exata e, portanto, o resto deve ser zero.

Então, como o polinômio divisor é

$(x+2),$

Pelo teorema do fator e pelo teorema do resto, sabemos que o polinômio

$P(x)$

será divisível pelo polinômio

$Q(x)$

se estiver preenchido

$P(-2)=0.$

Devemos, portanto, ver se esta igualdade se verifica:

$P(-2)=0 \quad \color{blue} \bm{?}$

$\begin{aligned} P(-2) &=-2\cdot (-2)^3-5\cdot (-2)^2-(-2)+2\\[2ex] &=-2 \cdot (-8) -5 \cdot 4+2 +2\\[2ex] & =16-20+2+2 \\[2ex] & =0\end{aligned}$

Na verdade, o resto da divisão

$\cfrac{P(x)}{Q(x)}$

é igual a 0, então o polinômio

$P(x)$

Sim, é divisível pelo outro polinômio

$Q(x).$

O que você acha da explicação? Você gostou? Esperemos! Não se esqueça que você pode nos deixar suas sugestões ou dúvidas nos comentários. Lemos todos vocês!

Teorema do resto (ou resíduo)

Qual é o teorema do resto?

Exemplo do teorema do resto

Teorema do resto e do fator

Exercícios resolvidos do teorema do resto

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Deixe um comentário Cancelar resposta