Regra de Cramer

Nesta página você verá o que é a regra de Cramer e, além disso, encontrará exemplos e exercícios com resolução de sistemas de equações pela regra de Cramer.

Qual é a regra de Cramer?

A regra de Cramer é um método usado para resolver sistemas de equações por determinantes. Vamos ver como é usado:

Considere um sistema de equações:

$\begin{cases} ax+by+cz= \color{red}\bm{j} \\[1.5ex] dx+ey+fz=\color{red}\bm{k} \\[1.5ex] gx+hy+iz = \color{red}\bm{l} \end{cases}$

A matriz A e a matriz estendida A’ do sistema são:

$\displaystyle A= \left( \begin{array}{ccc} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} a & b & c & \color{red}\bm{j} \\[1.1ex] d & e & f & \color{red}\bm{k} \\[1.1ex] g & h & i & \color{red}\bm{l} \end{array} \right)$

A regra de Cramer diz que a solução de um sistema de equações é:

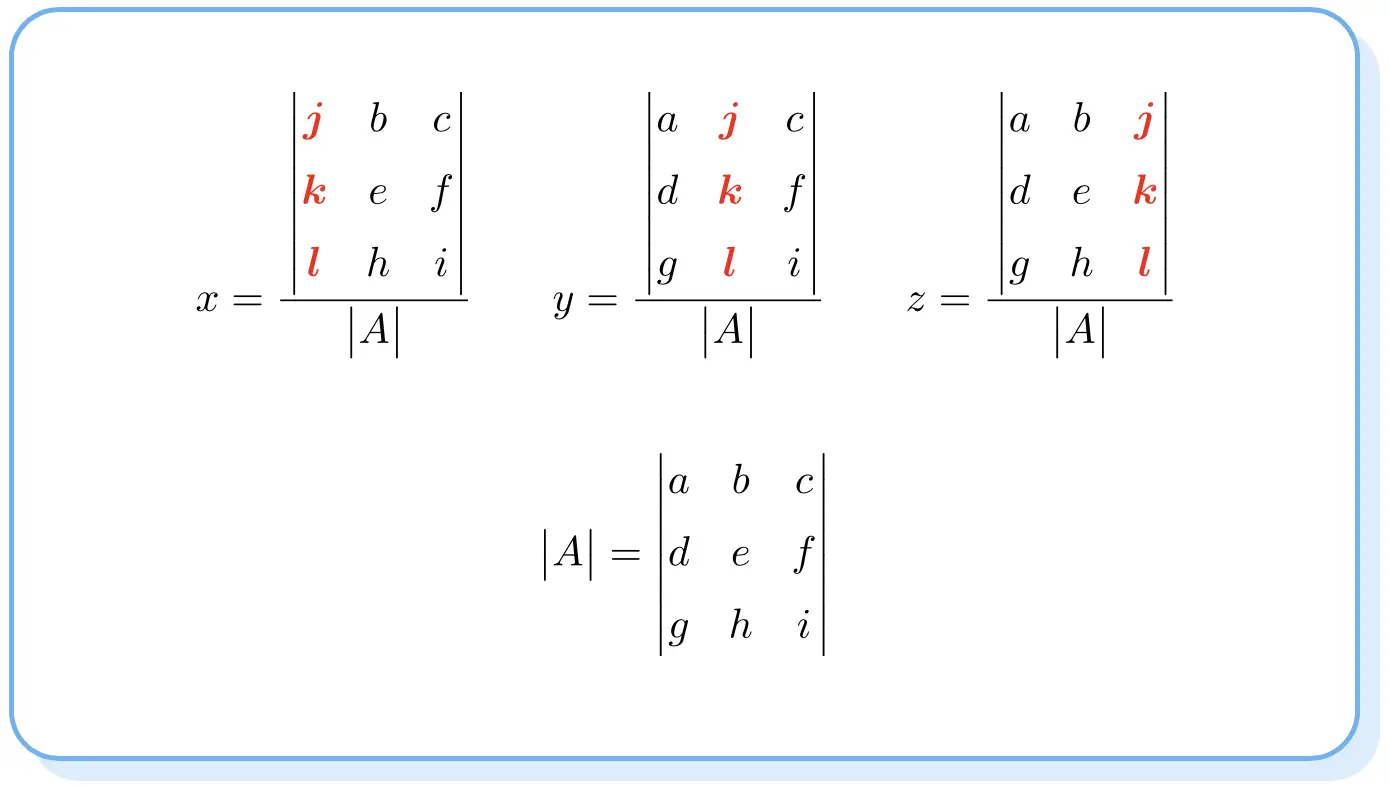
o que é a regra de Cramer, explicação da regra de Cramer

Observe que os determinantes dos numeradores são como o determinante da matriz A, mas mudando a coluna de cada incógnita para a coluna dos termos independentes.

Portanto, a regra de Cramer é usada para resolver sistemas de equações lineares. Mas, como você já sabe, existem muitas maneiras de resolver um sistema de equações, por exemplo , o método de Gauss Jordan é bem conhecido.

Abaixo estão exemplos de resolução de sistemas de equações lineares com a regra de Cramer, ou às vezes também escrita como regra de Kramer.

Exemplo 1: sistema compatível determinado (SCD)

Resolva o seguinte sistema de 3 equações com 3 incógnitas usando a regra de Cramer:

$\begin{cases} 2x+y+3z= 1 \\[1.5ex] 3x-2y-z=0 \\[1.5ex] x+3y+2z = 5\end{cases}$

Primeiro fazemos a matriz A e a matriz estendida A’ do sistema:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & 1 \\[1.1ex] 3 & -2 & -1 & 0 \\[1.1ex] 1 & 3 & 2 & 5 \end{array} \right)$

Calculamos agora a classificação das duas matrizes, para ver que tipo de sistema é. Para calcular a classificação de A, calculamos o determinante 3×3 de toda a matriz (usando a regra de Sarrus) e vemos se dá 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =-8-1+27+6+6-6 = 24 \neq 0$

O determinante de A é diferente de 0, então a matriz A tem classificação 3.

$\displaystyle rg(A)=3$

Portanto , a matriz A’ também é de posto 3 , uma vez que não pode ser de posto 4 e deve ter pelo menos o mesmo posto que a matriz A.

$\displaystyle rg(A')=3$

A extensão da matriz A é igual à extensão da matriz A’ e ao número de incógnitas do sistema (3), portanto, pelo teorema de Rouché-Frobenius , sabemos que se trata de um sistema compatível determinado (SCD):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Uma vez sabendo que o sistema é um SCD, aplicamos a regra de Cramer para resolvê-lo. Para fazer isso, lembre-se que a matriz A, seu determinante e a matriz A’ são:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & -1 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & 2 & \color{red}\bm{5} \end{array} \right)$

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =24$

Para calcular o desconhecido

$\displaystyle x$

Com a regra de Cramer, trocamos a primeira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} \color{red}\bm{1} & 1 & 3 \\[1.1ex] \color{red}\bm{0} & -2 & -1 \\[1.1ex] \color{red}\bm{5} & 3 & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{24}{24} = \bm{1}$

Para calcular o desconhecido

$\displaystyle y$

Com a regra de Cramer, trocamos a segunda coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 2 & \color{red}\bm{1} & 3 \\[1.1ex] 3 & \color{red}\bm{0} & -1 \\[1.1ex] 1 & \color{red}\bm{5} & 2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{48}{24} = \bm{2}$

Calcular

$\displaystyle z$

Com a regra de Cramer, trocamos a terceira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 2 & 1 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & \color{red}\bm{5}\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-24}{24} = \bm{-1}$

A solução do sistema de equações é, portanto:

$\displaystyle \bm{x = 1 \qquad y=2 \qquad z = -1}$

Exemplo 2: Sistema Compatível Indeterminado (ICS)

Resolva o seguinte sistema de equações usando a regra de Cramer:

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex] x+5y+3z = 1 \end{cases}$

Primeiro fazemos a matriz A e a matriz estendida A’ do sistema:

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & 2 & 4 & 1 \\[1.1ex] -2 & 3 & -1 & 0 \\[1.1ex] 1 & 5 & 3 & 1 \end{array} \right)$

Agora calculamos o contradomínio das duas matrizes e assim podemos ver que tipo de sistema é. Para calcular o posto de A, calculamos o determinante de toda a matriz (usando a regra de Sarrus) e verificamos se é 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3\end{vmatrix} = 27-2-40-12+15+12= 0$

O determinante dá 0, então a matriz A não é de posto 3. Mas tem um determinante 2×2 diferente de 0:

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

Portanto, a matriz A tem classificação 2 :

$\displaystyle rg(A)=2$

Uma vez conhecida a extensão da matriz A, calculamos a da matriz A’. O determinante das 3 primeiras colunas dá 0, então tentamos os outros determinantes 3×3 possíveis na matriz A’:

$\displaystyle \begin{vmatrix} 2 & 4 & 1 \\[1.1ex] 3 & -1 & 0 \\[1.1ex] 5 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 4 & 1 \\[1.1ex] -2 & -1 & 0 \\[1.1ex] 1 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 2 & 1 \\[1.1ex] -2 & 3 & 0 \\[1.1ex] 1 & 5 & 1 \end{vmatrix} = 0$

Todos os determinantes de ordem 3 dão 0. Mas, obviamente, a matriz A’ tem o mesmo determinante não-0 2×2 que a matriz A:

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

Portanto, a matriz A’ também é de posto 2 :

$\displaystyle rg(A')=2$

Assim, como o posto da matriz A é igual ao posto da matriz A’ mas estes dois são menores que o número de incógnitas do sistema (3), sabemos pelo teorema de Rouché-Frobenius que este é um sistema indeterminadamente compatível (ICS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

Quando queremos resolver um sistema indeterminado compatível (SCI), precisamos transformar o sistema : primeiro eliminamos uma equação, depois convertemos uma variável em λ (geralmente a variável z) e, finalmente, colocamos os termos com λ juntos com os termos independentes.

Uma vez transformado o sistema, aplicamos a regra de Cramer e obteremos a solução do sistema em função de λ.

Neste caso, eliminaremos a última equação do sistema:

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex]\cancel{x+5y+3z = 1} \end{cases} \longrightarrow \quad \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0\end{cases}$

Agora vamos converter a variável z em λ:

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x+2y+4\lambda=1 \\[1.5ex] -2x+3y-\lambda=0\end{cases}$

E colocamos os termos com λ com os termos independentes:

$\begin{cases} 3x+2y=1-4\lambda \\[1.5ex] -2x+3y=\lambda \end{cases}$

Portanto, a matriz A e a matriz A’ do sistema permanecem:

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 \\[1.1ex] -2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & 2 & 1 -4\lambda \\[1.1ex] -2 & 3 & \lambda \end{array} \right)$

Finalmente, uma vez transformado o sistema, aplicamos a regra de Cramer . Portanto, resolvemos o determinante de A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3\end{vmatrix} = 13$

Para calcular o desconhecido

$\displaystyle x$

Com a regra de Cramer, trocamos a primeira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1 -4\lambda & 2 \\[1.1ex] \lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3(1-4\lambda) -2\lambda}{13} = \cfrac{\bm{3-14\lambda} }{\bm{13}}$

Para calcular o desconhecido

$\displaystyle y$

Com a regra de Cramer, trocamos a segunda coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 1 -4\lambda \\[1.1ex]-2& \lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3\lambda -\bigl(-2(1-4\lambda)\bigr)}{13}= \cfrac{3\lambda -\bigl(-2+8\lambda\bigr)}{13} = \cfrac{\bm{2-5\lambda} }{\bm{13}}$

Embora a solução do sistema de equações seja função de λ, por ser um SCI e, portanto, possui infinitas soluções:

$\displaystyle \bm{x =} \cfrac{\bm{3-14\lambda} }{\bm{13}} \qquad \bm{y=}\cfrac{\bm{2-5\lambda} }{\bm{13}} \qquad \bm{z = \lambda}$

Regra de Cramer resolveu problemas

Exercício 1

Aplique a regra de Cramer para resolver o seguinte sistema de duas equações com 2 incógnitas:

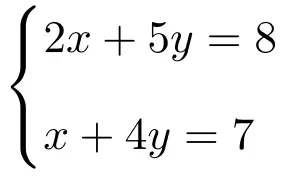
exercício resolvido passo a passo com a regra 2x2 de Cramer

veja solução

A primeira coisa a fazer é a matriz A e a matriz estendida A’ do sistema:

$\displaystyle A= \left( \begin{array}{cc} 2 & 5 \\[1.1ex] 1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 2 & 5 & 8 \\[1.1ex] 1 & 4 & 7 \end{array}\right)$

Devemos agora encontrar o posto da matriz A. Para isso, verificamos se o determinante de toda a matriz é diferente de 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-5=3 \bm{\neq 0}$

Como a matriz tem um determinante 2×2 diferente de 0, a matriz A tem posto 2:

$\displaystyle rg(A)=2$

Uma vez conhecida a classificação de A, calculamos a classificação de A’. Este será pelo menos de posto 2, pois acabamos de ver que tem dentro de um determinante de ordem 2 diferente de 0. Além disso, não pode ser de posto 3, pois não podemos deixar de fazer um determinante 3×3. Portanto, a matriz A’ também é de posto 2:

$\displaystyle rg(A')=2$

Portanto, aplicando o teorema de Rouché-Frobenius, sabemos que este é um sistema determinado compatível (SCD), pois o contradomínio de A é igual ao contradomínio de A’ e ao número de incógnitas.

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 2 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 2 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Uma vez sabendo que o sistema é um SCD, aplicamos a regra de Cramer para resolvê-lo.

Para calcular o desconhecido

$\displaystyle x$

Com a regra de Cramer, trocamos a primeira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 \\[1.1ex] 7 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-3}{3} = \bm{-1}$

Para calcular o desconhecido

$\displaystyle y$

Com a regra de Cramer, trocamos a segunda coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}2 & 8 \\[1.1ex] 1 & 7\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{6}{3} = \bm{2}$

A solução do sistema de equações é, portanto:

$\displaystyle \bm{x = -1 \qquad y=2}$

Exercício 2

Encontre a solução do seguinte sistema de três equações com 3 incógnitas usando a regra de Cramer:

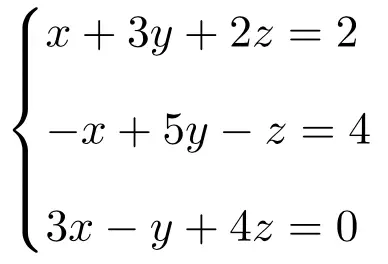
Exercício resolvido da regra de Cramer de um sistema de equações 3x3

veja solução

Primeiro fazemos a matriz A e a matriz estendida A’ do sistema:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 3 & 2\\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 3 & 2 & 2 \\[1.1ex] -1 & 5 & -1 & 4 \\[1.1ex] 3 & -1 & 4 & 0 \end{array}\right)$

Agora encontramos a classificação da matriz A calculando o determinante da matriz 3×3 com a regra de Sarrus:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{vmatrix} = 20-9+2-30-1+12=-6 \bm{\neq 0}$

A matriz tendo um determinante de ordem 3 diferente de 0, a matriz A é de posto 3:

$\displaystyle rg(A)=3$

conseqüentemente, a matriz A’ também é de classificação 3:

$\displaystyle rg(A')=3$

Portanto, utilizando o teorema de Rouché-Frobenius, sabemos que este é um sistema determinado compatível (SCD), pois o contradomínio de A é igual ao contradomínio de A’ e ao número de incógnitas.

Uma vez sabendo que o sistema é um SCD, precisamos aplicar a regra de Cramer para resolver o sistema.

Para calcular o desconhecido

$\displaystyle x$

Com a regra de Cramer, trocamos a primeira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 & 3 & 2 \\[1.1ex] 4 & 5 & -1\\[1.1ex]0 & -1 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-18}{-6} = \bm{3}$

Para calcular o desconhecido

$\displaystyle y$

Com a regra de Cramer, trocamos a segunda coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 4 & -1\\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-6}{-6} = \bm{1}$

Calcular

$\displaystyle z$

Com a regra de Cramer, trocamos a terceira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 3 & -1 & 0\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12}{-6} = \bm{-2}$

A solução do sistema de equações é, portanto:

$\displaystyle \bm{x =3 \qquad y=1 \qquad z=-2}$

Exercício 3

Calcule a solução do seguinte sistema de três equações com 3 incógnitas usando a regra de Cramer:

veja solução

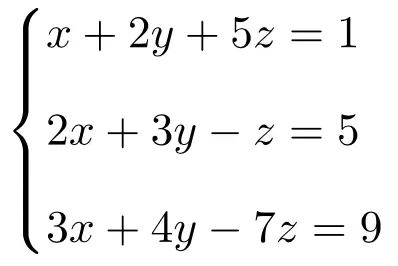
Primeiro fazemos a matriz A e a matriz estendida A’ do sistema:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 2 & 5 & 1 \\[1.1ex] 2 & 3 & -1 & 5 \\[1.1ex] 3 & 4 & -7 & 9 \end{array}\right)$

Calculamos a extensão da matriz A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{vmatrix} =-21-6+40-45+4+28=0$

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

$\displaystyle rg(A)=2$

Uma vez conhecida a extensão da matriz A, calculamos a da matriz A’. O determinante das 3 primeiras colunas dá 0, então tentamos os outros determinantes 3×3 possíveis na matriz A’:

$\displaystyle \begin{vmatrix} 2 & 5 & 1 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 4 & -7 & 9 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 5 & 1 \\[1.1ex] 2 & -1 & 5 \\[1.1ex] 3 & -7 & 9\end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 1 \\[1.1ex] 2 & 3 & 5 \\[1.1ex] 3 & 4 & 9 \end{vmatrix} = 0$

Todos os determinantes de ordem 3 dão 0. No entanto, a matriz A’ tem o mesmo determinante 2×2 diferente de 0 que a matriz A:

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

Portanto, a matriz A’ também é de posto 2:

$\displaystyle rg(A')=2$

Como o posto da matriz A é igual ao posto da matriz A’ mas estes dois são menores que o número de incógnitas do sistema (3), sabemos pelo teorema de Rouché-Frobenius que se trata de um Sistema Compatível Indeterminado (ICS):

Sendo um sistema ICS, temos que eliminar uma equação. Neste caso, eliminaremos a última equação do sistema:

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \\[1.5ex]\cancel{3x+4y-7z = 9} \end{cases} \longrightarrow \quad \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5\end{cases}$

Agora vamos converter a variável z em λ:

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+2y+5\lambda=1 \\[1.5ex] 2x+3y-\lambda=5\end{cases}$

E colocamos os termos com λ com os termos independentes:

$\begin{cases} x+2y=1-5\lambda\\[1.5ex] 2x+3y=5+\lambda \end{cases}$

Tal que a matriz A e a matriz A’ do sistema permanecem:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 \\[1.1ex] 2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 2 & 1 -5\lambda \\[1.1ex] 2 & 3 &5+\lambda \end{array} \right)$

Finalmente, uma vez transformado o sistema, aplicamos a regra de Cramer . Portanto, resolvemos o determinante de A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3\end{vmatrix} =-1$

Para calcular o desconhecido

$\displaystyle x$

Com a regra de Cramer, trocamos a primeira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1-5\lambda & 2 \\[1.1ex] 5+\lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3-15\lambda -(10+2\lambda)}{-1} = \cfrac{-7-17\lambda}{-1} = \bm{7+17\lambda}$

Para calcular o desconhecido

$\displaystyle y$

Com a regra de Cramer, trocamos a segunda coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 1-5\lambda \\[1.1ex] 2 & 5+\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{5+\lambda -(2-10\lambda)}{-1}= \cfrac{3+11\lambda}{-1} = \bm{-3-11\lambda}$

Embora a solução do sistema de equações seja função de λ, por ser um SCI e, portanto, possui infinitas soluções:

$\displaystyle \bm{x =7+17\lambda} \qquad \bm{y=-3-11\lambda} \qquad \bm{z = \lambda}$

Exercício 4

Resolva o seguinte problema de um sistema de três equações com 3 incógnitas aplicando a regra de Cramer:

$\begin{cases} -2x+5y+z=8 \\[1.5ex] 6x+2y+4z=4 \\[1.5ex] 3x-2y+z = -2 \end{cases}$

veja solução

Primeiro, construímos a matriz A e a matriz estendida A’ do sistema:

$\displaystyle A= \left( \begin{array}{ccc}-2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} -2 & 5 & 1 & 8 \\[1.1ex] 6 & 2 & 4 & 4 \\[1.1ex] 3 & -2 & 1 & -2 \end{array}\right)$

Agora vamos calcular a classificação da matriz A calculando o determinante da matriz 3×3 usando a regra de Sarrus:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} -2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1 \end{vmatrix} = -4+60-12-6-16-30=-8 \bm{\neq 0}$

A matriz tendo um determinante de ordem 3 diferente de 0, a matriz A é de posto 3:

$\displaystyle rg(A)=3$

conseqüentemente, a matriz A’ também é de posto 3, pois deve ser pelo menos do mesmo posto que a matriz A e não pode ser de posto 4 porque é uma matriz de dimensão 3×4.

$\displaystyle rg(A')=3$

Portanto, utilizando o teorema de Rouché-Frobenius, deduzimos que se trata de um sistema compatível determinado (SCD), pois o contradomínio de A é igual ao contradomínio de A’ e ao número de incógnitas.

Uma vez sabendo que o sistema é um SCD, precisamos aplicar a regra de Cramer para resolver o sistema.

Para calcular o desconhecido

$\displaystyle x$

Com a regra de Cramer, trocamos a primeira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 & 1 \\[1.1ex] 4 & 2 & 4 \\[1.1ex] -2 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{16}{-8} = \bm{-2}$

Para calcular o desconhecido

$\displaystyle y$

Com a regra de Cramer, trocamos a segunda coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}-2 & 8 & 1 \\[1.1ex] 6 & 4 & 4 \\[1.1ex] 3 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-6} = \bm{0}$

Calcular

$\displaystyle z$

Com a regra de Cramer, trocamos a terceira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} -2 & 5 & 8 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & -2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-32}{-8} = \bm{4}$

A solução do sistema de equações lineares é, portanto:

$\displaystyle \bm{x =-2 \qquad y=0 \qquad z=4}$

Exercício 5

Resolva o seguinte sistema de equações lineares usando a regra de Cramer:

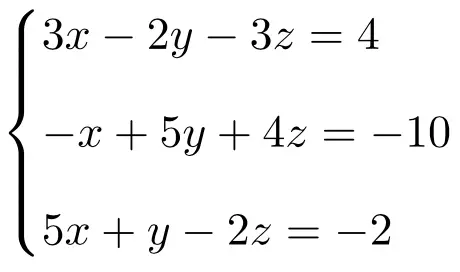
Exemplo de resolução de um sistema de equações com a regra de Cramer

veja solução

Primeiro fazemos a matriz A e a matriz estendida A’ do sistema:

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -2 & -3 & 4 \\[1.1ex] -1 & 5 & 4 & -10 \\[1.1ex] 5 & 1 & -2 & -2 \end{array}\right)$

Calculamos a extensão da matriz A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{vmatrix} =-30-40+3+75-12+4=0$

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 15- (2)= 13 \neq 0$

$\displaystyle rg(A)=2$

Uma vez conhecida a extensão da matriz A, calculamos a da matriz A’. O determinante das 3 primeiras colunas dá 0, então tentamos os outros determinantes 3×3 possíveis na matriz A’:

$\displaystyle \begin{vmatrix} -2 & -3 & 4 \\[1.1ex] 5 & 4 & -10 \\[1.1ex] 1 & -2 & -2 \end{vmatrix} = 0 \qquad \begin{vmatrix}3 & -3 & 4 \\[1.1ex] -1 & 4 & -10 \\[1.1ex] 5 & -2 & -2\end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & -2 & 4 \\[1.1ex] -1 & 5 & -10 \\[1.1ex] 5 & 1 &-2\end{vmatrix} = 0$

Todos os determinantes de ordem 3 dão 0. Mas, obviamente, a matriz A’ tem o mesmo determinante de ordem 2 diferente de 0 que a matriz A:

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 13 \neq 0$

Portanto, a matriz A’ também é de posto 2:

$\displaystyle rg(A')=2$

O posto da matriz A é igual ao posto da matriz A’ mas estes dois são menores que o número de incógnitas do sistema (3), então pelo teorema de Rouché-Frobenius sabemos que se trata de um Sistema Indeterminado Compatível (SCI) :

Sendo um sistema ICS, temos que eliminar uma equação. Neste caso, eliminaremos a última equação do sistema:

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \\[1.5ex]\cancel{5x+y-2z = -2} \end{cases} \longrightarrow \quad \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10\end{cases}$

Agora vamos converter a variável z em λ:

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x-2y-3\lambda=4 \\[1.5ex] -x+5y+4\lambda=-10\end{cases}$

E colocamos os termos com λ com os termos independentes:

$\begin{cases} 3x-2y=4+3\lambda \\[1.5ex] -x+5y=-10-4\lambda\end{cases}$

Tal que a matriz A e a matriz A’ do sistema permanecem:

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 \\[1.1ex] -1 & 5 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & -2 & 4+3\lambda \\[1.1ex] 1 & 5 &-10-4\lambda \end{array} \right)$

Finalmente, uma vez transformado o sistema, aplicamos a regra de Cramer . Portanto, resolvemos o determinante de A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}3& -2 \\[1.1ex] -1 & 5\end{vmatrix} =13$

Para calcular o desconhecido

$\displaystyle x$

Com a regra de Cramer, trocamos a primeira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 4+3\lambda & -2 \\[1.1ex]-10-4\lambda & 5\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{20+15\lambda -(20+8\lambda)}{13} = \cfrac{\bm{7\lambda}}{\bm{13}}$

Para calcular o desconhecido

$\displaystyle y$

Com a regra de Cramer, trocamos a segunda coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 4+3\lambda \\[1.1ex] -1 & -10-4\lambda\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-30-12\lambda -(-4-3\lambda)}{13}= \cfrac{\bm{-26-9\lambda}}{\bm{13}}$

Assim, a solução do sistema de equações é função de λ, pois é um SCI e, portanto, o sistema possui infinitas soluções:

$\displaystyle \bm{x=} \cfrac{\bm{7\lambda}}{\bm{13}} \qquad \bm{y=} \cfrac{\bm{-26-9\lambda}}{\bm{13}} \qquad \bm{z = \lambda}$

Qual é a regra de Cramer?

Exemplo 1: sistema compatível determinado (SCD)

Exemplo 2: Sistema Compatível Indeterminado (ICS)

Regra de Cramer resolveu problemas

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Deixe um comentário Cancelar resposta