Produto misto de três vetores (ou produto escalar triplo)

Nesta página explicamos o que é o produto misto de três vetores (ou produto escalar triplo) e como ele é calculado. Você também verá exemplos, exercícios e problemas resolvidos sobre este tipo de operação entre vetores. E, além disso, você encontrará as propriedades e aplicações do produto misto.

Qual é o produto misto de três vetores?

O produto misto de três vetores, também chamado de produto escalar triplo , é uma multiplicação sucessiva entre três vetores envolvendo dois tipos diferentes de operações: o produto escalar e o produto vetorial . Portanto, a combinação das duas operações vetoriais dá um escalar (um número real).

Concretamente, o produto misto consiste em calcular o produto vetorial de dois vetores e, posteriormente, multiplicar vetorialmente o resultado obtido por um terceiro vetor. Escrito assim pode parecer muito complicado, mas na realidade não é tanto assim, veja a fórmula do produto escalar triplo:

\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})

Como você pode ver em sua fórmula, o produto misto de três vetores é indicado por dois colchetes.

Como calcular o produto misto de três vetores?

A fórmula do produto escalar triplo é a que acabamos de ver na seção anterior, porém, geralmente não é usada para determinar o produto misto de três vetores porque existe outra maneira, mais simples e rápida:

Sejam quaisquer 3 vetores:

\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)\qquad \vv{\text{w}}= (\text{w}_x,\text{w}_y,\text{w}_z)

Para calcular o produto misto entre três vetores, basta resolver o determinante 3×3 formado pelas componentes dos vetores:

\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \\[1.1ex] \text{w}_x & \text{w}_y & \text{w}_z \end{vmatrix}

Para que você possa ver um exemplo de como isso é calculado , encontraremos o produto misto dos três vetores a seguir:

\vv{\text{u}}= (1,2,0) \qquad \vv{\text{v}}= (0,-1,3)\qquad \vv{\text{w}}= (-2,4,1)

Para determinar o produto misto, construímos um determinante de ordem 3 colocando os vetores nas linhas da matriz:

\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}

E agora só precisamos resolver o determinante da matriz, para isso você pode usar qualquer método. Neste caso, aplicaremos a regra de Sarrus (mas isso também pode ser feito por adições ou cofatores):

\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \\[2ex] &= -1-12+0-0-12-0 \\[2ex] & = \bm{-25} \end{aligned}

Para mostrar que os dois procedimentos são equivalentes, calcularemos o produto misto dos mesmos vetores por meio de sua definição:

\begin{aligned} \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] & = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})\\[2ex] &=(1,2,0) \cdot \Bigl( (0,-1,3)\times (-2,4,1)\Bigr) \\[2ex] & = (1,2,0) \cdot \begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 0& -1 & 3 \\[1.1ex] -2 &4&1 \end{vmatrix} \\[2ex] &= (1,2,0) \cdot (-13,-6,-2) \\[2ex] & = \bm{-25} \end{aligned}

Recomendamos calcular o produto misto através do determinante dos vetores, pois é mais rápido e há menos chances de erros. Mas, como você pode ver, o resultado é o mesmo, não importa o método usado, então use o que preferir. 👍

Interpretação geométrica do produto misto

Depois de saber como encontrar o produto misto de três vetores, você deve estar se perguntando… e para que serve o produto misto? Pois bem, em matemática tem dois usos principais: calcular o volume de um paralelepípedo e o volume de um tetraedro.

O volume de um paralelepípedo é igual ao valor absoluto do produto misto dos vetores que marcam as 3 dimensões do campo geométrico.

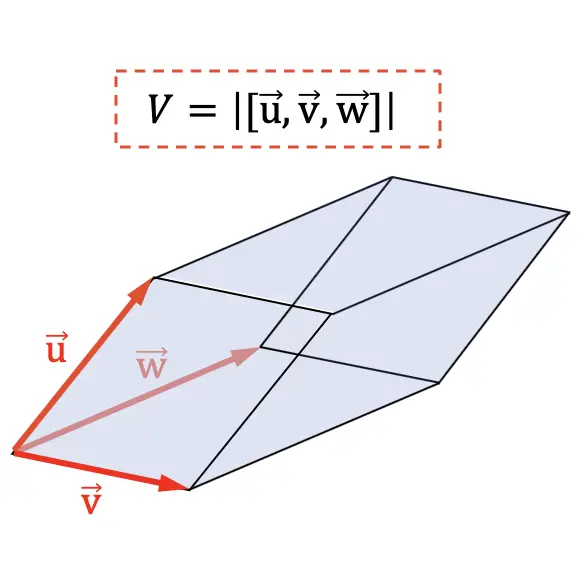
exemplo de produto misto de três vetores ou produto escalar triplo

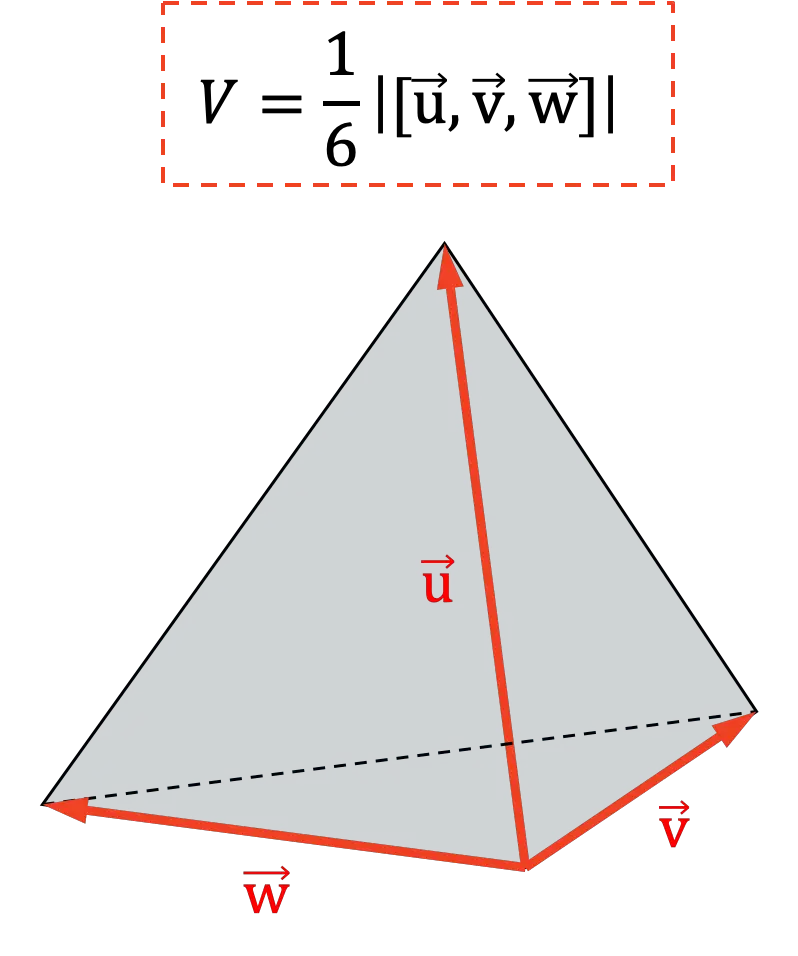
Outra aplicação do produto misto é determinar o volume de um tetraedro . Visto que geometricamente a sexta parte do valor absoluto do produto misto representa o volume de um tetraedro:

produto misto de três vetores em r3

Propriedades do produto misto ou produto escalar triplo

O produto misto, ou produto escalar triplo, possui as seguintes características:

  • Em geral, uma mudança na ordem dos vetores de produtos mistos também implica uma mudança no sinal. Portanto, a ordem dos vetores de produtos mistos é importante.

\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = -\bigl[\vv{\text{v}},\vv{\text{u}},\vv{\text{w}}\bigr] = -\bigl[\vv{\text{u}},\vv{\text{w}},\vv{\text{v}}\bigr] = - \bigl[\vv{\text{w}},\vv{\text{v}},\vv{\text{u}}\bigr]

  • Porém, se mudarmos a ordem ciclicamente , o sinal não muda:

\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \bigl[\vv{\text{v}},\vv{\text{w}},\vv{\text{u}}\bigr] = \bigl[\vv{\text{w}},\vv{\text{u}},\vv{\text{v}}\bigr]

  • Num espaço tridimensional (em R3), o produto misto de três vetores linearmente dependentes ou coplanares (pertencentes ao mesmo plano) é igual a 0.

Corrigidos problemas de produtos mistos

Exercício 1

Dados 3 vetores:

\vv{\text{u}}= (3,-1,2) \qquad \vv{\text{v}}= (-2,0,1)\qquad \vv{\text{w}}= (5,1,-1)

Calcule o produto misto dos três vetores:

\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]

Para encontrar o seu produto misto, devemos resolver o determinante composto pelas coordenadas dos vetores:

\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & -1 & 2 \\[1.1ex] -2 & 0 & 1 \\[1.1ex] 5 & 1 & -1 \end{vmatrix} \\[2ex] &= 0-5-4-0-3+2 \\[2ex] & = \bm{-10} \end{aligned}

Exercício 2

Dados 3 vetores:

\vv{\text{u}}= (7,2,-3) \qquad \vv{\text{v}}= (2,4,9)\qquad \vv{\text{w}}= (4,3,-1)

Determine o produto misto entre os três vetores:

\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]

Para encontrar seu produto misto, precisamos resolver o determinante que tem as coordenadas cartesianas dos vetores em forma de linha:

\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 7 & 2 & -3 \\[1.1ex] 2 & 4 & 9 \\[1.1ex] 4 & 3 & -1 \end{vmatrix} \\[2ex] &= -28+72-18+48-189+4 \\[2ex] & = \bm{-111} \end{aligned}

Exercício 3

Calcule o volume do paralelepípedo cujos 3 lados são os seguintes vetores:

\vv{\text{u}}= (0,2,5) \qquad \vv{\text{v}}= (-1,6,2)\qquad \vv{\text{w}}= (3,1,2)

O volume de um paralelepípedo é igual ao valor absoluto do produto misto de 3 dos vetores que ele tem como arestas. Portanto, primeiro calculamos o produto vetorial triplo dos vetores:

\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 0 & 2 & 5 \\[1.1ex] -1 & 6 & 2 \\[1.1ex] 3 & 1 & 2 \end{vmatrix} \\[2ex] &= 0+12-5-90-0+4 \\[2ex] & = -79 \end{aligned}

Para que o volume do paralelepípedo seja o valor absoluto do resultado do produto misto:

V= \lvert -79 \rvert = \bm{79}\ \mathbf{u}\bm{^3}

Exercício 4

Calcule o volume do tetraedro cujos vértices são os seguintes pontos:

A(1,0,2) \qquad B(3,3,2)\qquad C(5,-1,4)\qquad D(4,2,1)

Primeiro, calculamos os vetores que representam as arestas do tetraedro:

\vv{AB}=B-A= (3,3,2)-(1,0,2)=(2,3,0)

\vv{AC}=C-A= (5,-1,4)-(1,0,2)=(4,-1,2)

\vv{AD}=D-A= (4,2,1)-(1,0,2)=(3,2,-1)

O volume de um tetraedro equivale a um sexto do valor absoluto do produto misto de 3 dos vetores que ele possui para as arestas. Portanto, primeiro calculamos o produto misto dos vetores encontrados:

\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 2 & 3 & 0 \\[1.1ex] 4 & -1 & 2 \\[1.1ex] 3 & 2 & -1 \end{vmatrix} \\[2ex] &= 2+18+0-0-8+12 \\[2ex] & = 24 \end{aligned}

Assim, o volume do tetraedro será um sexto do valor absoluto do produto misto:

V= \cfrac{1}{6} \cdot \lvert 24 \rvert = \cfrac{24}{6} = \bm{4} \ \mathbf{u}\bm{^3}

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima