Pontos coplanares (ou coplanares)

Nesta página você descobrirá o que são pontos coplanares (ou coplanares) e como saber se determinados pontos são coplanares ou não. Além disso, você poderá ver exemplos e praticar com exercícios de pontos coplanares resolvidos.

O que são pontos coplanares?

Na geometria analítica, o significado dos pontos coplanares (ou coplanares) é o seguinte:

Pontos coplanares são pontos que pertencem ao mesmo plano.

Portanto, 2 ou 3 pontos são sempre coplanares porque um plano pode ser formado com apenas 3 pontos. Por outro lado, quando existem 4, 5 ou mais pontos, é possível que alguns dos pontos não estejam contidos no mesmo plano e, portanto, não sejam coplanares.

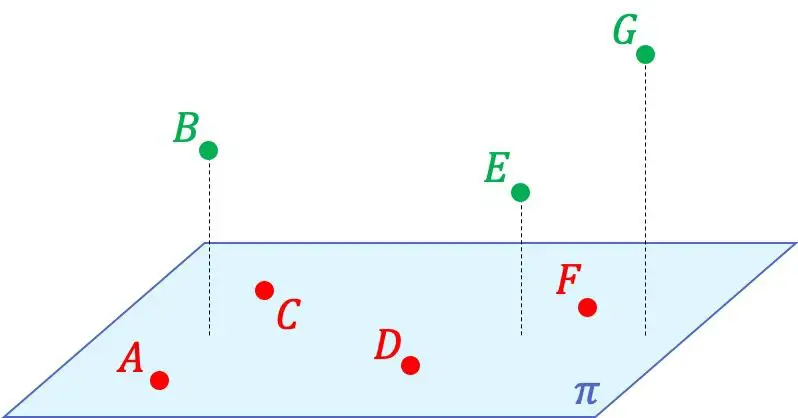
Por exemplo, na representação gráfica acima, você pode ver que os pontos A, C, D e F são coplanares entre si, pois estão contidos no mesmo plano. Por outro lado, estes 4 pontos não são coplanares com os pontos B, E e G, porque nenhum plano pode ser formado no espaço que contém todos os pontos.

Desta propriedade podemos deduzir que os vetores definidos por pontos coplanares também são vetores coplanares, ou seja, estão contidos no mesmo plano.

Quando os pontos são coplanares?

Como vimos na definição de pontos coplanares (ou coplanares), dois ou três pontos são sempre coplanares, mas mais de três pontos não precisam respeitar a relação de coplanaridade.

Portanto, existem basicamente 2 métodos para determinar se quatro ou mais pontos são coplanares:

Uma forma de saber se os pontos são coplanares é pelos vetores que são determinados pelos pontos: se esses vetores são coplanares , então os pontos também são coplanares.

Obviamente, para aplicar este método é necessário saber quando os vetores são coplanares. Mas como também existem várias maneiras de determinar se um conjunto de vetores é coplanar, recomendamos verificar como saber se os vetores são coplanares . Aqui você encontrará todos os procedimentos existentes para descobrir quando 2, 3, 4 ou mais vetores são coplanares, além de exemplos e exercícios resolvidos.

Outra forma de saber se um conjunto de pontos é coplanar é encontrar a equação do plano formado por 3 pontos do conjunto, e se os demais pontos satisfazem esta equação, então isso significa que todos os pontos do conjunto são coplanares.

Embora dependa do problema, recomendamos utilizar o primeiro dos dois métodos, pois é muito mais simples e rápido verificar se os vetores são coplanares do que calcular a equação de um plano. Mas, obviamente, use o que preferir.

Problemas de pontos coplanares resolvidos

Exercício 1

Determine se os três pontos a seguir são coplanares:

$A(3,5,1)$

$B(0,-2,3)$

$C(4,-1,2)$

veja solução

Neste caso não é necessário fazer nenhum cálculo porque 3 pontos são sempre coplanares , sejam eles quais forem.

Exercício 2

Determine se os quatro pontos a seguir são coplanares:

$A(1,2,0)$

$B(-1,3,4)$

$C(1,0,-1)$

$D(2,5,-3)$

veja solução

Para que os quatro pontos sejam coplanares, os vetores por eles determinados devem ser coplanares. Portanto, calculamos estes vetores:

$\vv{AB} = B- A = (-1,3,4)-(1,2,0) = (-2,1,4)$

$\vv{AC} = C- A = (1,0,-1)-(1,2,0) = (0,-2,-1)$

$\vv{AD} = D- A = (2,5,-3)-(1,2,0) = (1,3,-3)$

Vamos agora construir a matriz formada pelos vetores:

$\displaystyle A= \begin{pmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{pmatrix}$

Para que os vetores resultantes sejam coplanares, o posto da matriz anterior deve ser igual a 2. E, para isso, o determinante de toda a matriz 3×3 deve ser igual a zero:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{vmatrix} =-11\neq 0$

$rg(A)=3$

Porém, o determinante de toda a matriz é diferente de zero, então o posto da matriz é 3 e, portanto , os 4 pontos não são coplanares .

Exercício 3

Descubra se os cinco pontos a seguir são coplanares:

$A(3,1,1)$

$B(0,0,2)$

$C(4,-2,-1)$

$D(-1,1,3)$

$E(2,4,3)$

veja solução

Para que todos os cinco pontos sejam coplanares, os vetores por eles definidos devem ser coplanares. Portanto, calculamos estes vetores:

$\vv{AB} = B- A = (0,0,2)-(3,1,1) = (-3,-1,1)$

$\vv{AC} = C- A = (4,-2,-1)-(3,1,1) = (1,-3,-2)$

$\vv{AD} = D- A = (-1,1,3)-(3,1,1) = (-4,0,2)$

$\vv{AE} = E- A = (2,4,3)-(3,1,1) = (-1,3,2)$

Vamos agora construir a matriz composta pelos vetores:

$\displaystyle A= \begin{pmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{pmatrix}$

Para que os vetores resultantes sejam coplanares, o posto da matriz anterior deve ser igual a 2. Calculamos, portanto, o posto da matriz de vetores por determinantes para verificar se eles são coplanares:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\end{vmatrix} = 0 \qquad \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -1&3&2\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0 \qquad \begin{vmatrix} 1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} -3&-1 \\[1.1ex] 1&-3\end{vmatrix} =10\neq 0$

$rg(A)=2$

O posto da matriz é equivalente a 2, portanto os vetores são coplanares e portanto os 5 pontos também são coplanares.

Exercício 4

Calcular o valor do parâmetro

$k$

de modo que os 4 pontos a seguir sejam coplanares:

$A(3,1,4)$

$B(2,1,2)$

$C(0,-1,3)$

$D(3,2,k)$

veja solução

Para que os quatro pontos sejam coplanares, os vetores por eles determinados devem ser coplanares. Portanto, calculamos estes vetores:

$\vv{AB} = B- A = (2,1,2)-(3,1,4) = (-1,0,-2)$

$\vv{AC} = C- A = (0,-1,3)-(3,1,4) = (-3,-2,-1)$

$\vv{AD} = D- A = (3,2,k)-(3,1,4) = (0,1,k-4)$

Cuja matriz vetorial é:

$\displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}$

Para que os vetores resultantes sejam coplanares, o posto da matriz deve ser 2. E, portanto, o determinante de toda a matriz 3×3 deve ser 0:

$\displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0$

$\displaystyle 2k-3 =0$

Finalmente, resolvemos o desconhecido

$k:$

$2k =3$

$\bm{k =}\mathbf{\cfrac{3}{2}}$

Por fim, se este artigo foi útil para você, provavelmente você também está interessado em como é calculada a distância entre dois pontos (fórmula) , já que às vezes em problemas de geometria analítica nos perguntam qual é a distância entre dois pontos. Na página do link você encontrará uma explicação bem detalhada, além de exemplos e exercícios resolvidos passo a passo.

O que são pontos coplanares?

Quando os pontos são coplanares?

Problemas de pontos coplanares resolvidos

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Deixe um comentário Cancelar resposta