Matriz Nilpotente

Nesta página você encontrará uma explicação do que é uma matriz nilpotente, além de vários exemplos para que você possa entendê-la e não ter dúvidas. Além disso, você poderá ver as estruturas das matrizes nilpotentes e todas as propriedades desses tipos de matrizes.

O que é uma matriz nilpotente?

A definição de matriz nilpotente é a seguinte:

Uma matriz nilpotente é uma matriz quadrada que elevada a um número inteiro dá a matriz zero .

$N^k =0$

Ouro

$N$

é a matriz nilpotente e

$k$

o expoente da potência que dá a matriz zero.

Esta condição não significa que a potência de uma matriz nilpotente sempre dê zero independente do expoente, mas sim que se existir pelo menos uma potência da matriz cujo resultado seja uma matriz cheia de 0s, então a matriz é nilpotente.

Por outro lado, o índice de nilpotência de uma matriz nilpotente é o menor número com o qual a condição de nilpotência é satisfeita. Podemos dizer também que a matriz nilpotente é de ordem k , onde k é o seu índice de nilpotência.

Exemplos de matrizes nilpotentes

Para finalizar a compreensão do conceito de matriz nilpotente, veremos vários exemplos desse tipo de matriz:

Exemplo de uma matriz nilpotente 2 × 2

A seguinte matriz quadrada de dimensão 2×2 é nilpotente:

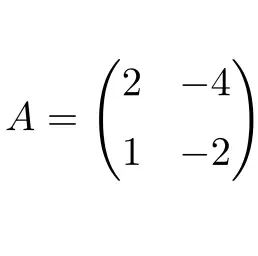
exemplo de uma matriz nilpotente de dimensão 2x2

A matriz é nilpotente porque ao elevar ao quadrado a matriz A obtemos como resultado a matriz zero:

$\displaystyle A^2=\begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}\cdot \begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}=\begin{pmatrix} \bm{0} &\bm{0} \\[1.1ex] \bm{0} & \bm{0} \end{pmatrix}$

É portanto uma matriz nilpotente e seu índice de nilpotência é 2, pois a matriz zero é obtida elevada à segunda potência.

Exemplo de uma matriz nilpotente 3×3

A seguinte matriz quadrada de ordem 3 é nilpotente:

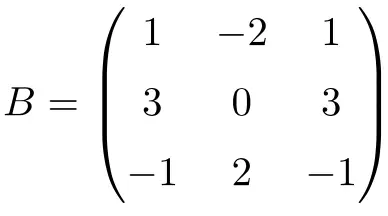
exemplo de uma matriz nilpotente de dimensão 3x3

Embora elevando a matriz para 2 não obtenhamos a matriz zero:

$\displaystyle B^2=\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}\cdot \begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}$

Mas ao calcular o cubo da matriz, obtemos uma matriz com todos os elementos iguais a 0:

$\displaystyle B^3= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}\cdot\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}\bm{0}&\bm{0}&\bm{0}\\[1.1ex]\bm{0}&\bm{0}&\bm{0}\\[1.1ex] \bm{0}&\bm{0}&\bm{0}\end{pmatrix}$

Portanto, a matriz B é uma matriz nilpotente, e como a matriz zero é elevada à potência de 3, seu índice de nilpotência é 3.

Estrutura de uma matriz nilpotente 2 × 2

Abaixo você pode ver a estrutura de todas as matrizes nilpotentes. Sua prova é um pouco tediosa, então deixamos para vocês diretamente a fórmula para obter uma matriz nilpotente de ordem 2:

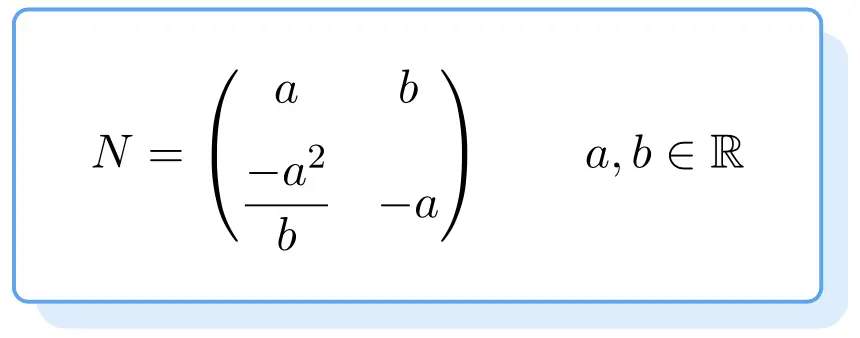
estrutura e fórmula de uma matriz nilpotente 2x2

Portanto, qualquer matriz que satisfaça a fórmula acima será uma matriz nilpotente. Para isso, os valores

$a$

$b$

eles podem ser arbitrários, desde que sejam números reais.

Propriedades de matrizes nilpotentes

As matrizes nilpotentes possuem as seguintes características:

O traço de uma matriz nilpotente é sempre zero.

Da mesma forma, o determinante de qualquer matriz nilpotente é sempre 0. Porém, o inverso não é verdadeiro, ou seja, o determinante de uma matriz é zero não implica que a matriz seja nilpotente.

A única matriz nilpotente que pode ser diagonalizada é a matriz zero.

O índice de nilpotência de uma matriz nilpotente de dimensão n×n é sempre igual ou menor que n . É por isso que o índice de nilpotência de uma matriz nilpotente 2 × 2 será sempre 2.

Uma matriz nilpotente não é invertível.

Qualquer matriz triangular com zeros na diagonal principal também é uma matriz nilpotente.

Existe um teorema que diz que se a matriz
$N$

é nilpotente, então a matriz

$N+I$

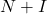
é invertível, onde

$I$

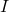
é a matriz identidade. Além disso, sua matriz inversa pode ser encontrada com a seguinte fórmula:

$\displaystyle(N+I)^{-1} = \sum_{m = 0}^\infty (-N)^m=I-N+N^2-N^3+\cdots$

Equivalentemente, se
$N$

é uma matriz nilpotente, então o inverso da matriz pode ser calculado

$N-I$

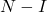
com a seguinte equação:

$\displaystyle(N-I)^{-1} = \sum_{m = 0}^\infty (N)^m=I+N+N^2+N^3+\cdots$

Qualquer matriz singular, ou seja, não invertível, pode ser decomposta no produto de matrizes nilpotentes.

Todos os autovalores (ou autovalores) de uma matriz nilpotente são zero.

$\displaystyle \lambda=0 \qquad \forall \ \lambda$

Por fim, a título de curiosidade, existe também o conceito de transformação nilpotente, que define uma aplicação linear
$L$

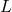
de um espaço vetorial tal que

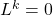
$L^k=0$

.