Matriz ortogonal - Matoridade

Nesta página você verá o que são matrizes ortogonais e a relação que elas têm com a inversa de uma matriz. Você também verá vários exemplos para entendê-lo perfeitamente. Além disso, ensinamos a fórmula que verifica qualquer matriz ortogonal, com a qual você saberá como encontrá-la rapidamente. E, finalmente, você encontrará as propriedades e aplicações dessas matrizes específicas, bem como um típico exercício de exame resolvido.

O que é uma matriz ortogonal?

A definição de matriz ortogonal é a seguinte:

Uma matriz ortogonal é uma matriz quadrada de números reais que multiplicada por sua transposta (ou transposta) é igual à matriz identidade. Ou seja, a seguinte condição é atendida:

$A\cdot A^t = A^t \cdot A =I$

Ouro

$A$

é uma matriz ortogonal e

$A^t$

representa sua matriz transposta.

Para que esta condição seja atendida, as colunas e linhas de uma matriz ortogonal devem ser vetores unitários ortogonais, ou seja, devem formar uma base ortonormal. Por esta razão, alguns matemáticos também as chamam de matrizes ortonormais .

Inversa de uma matriz ortogonal

Outra forma de explicar o conceito de matriz ortogonal é através da matriz inversa, pois a matriz transposta (ou transposta) de uma matriz ortogonal é igual à sua inversa.

Para compreender completamente este teorema, é importante que você saiba como inverter uma matriz . Neste link você encontrará uma explicação detalhada da inversa de uma matriz, todas as suas propriedades e ainda tem exercícios resolvidos passo a passo para praticar.

A matriz inversa de uma matriz ortogonal pode facilmente ser demonstrada como equivalente à sua transposta usando a condição da matriz ortogonal e a propriedade principal das matrizes inversas:

$\left.\begin{array}{c} A \cdot A^t =I \\[2ex] A \cdot A^{-1} = I\end{array} \right\} \longrightarrow \ A^t=A^{-1}$

Portanto, uma matriz ortogonal será sempre uma matriz invertível , ou seja, será uma matriz regular ou não degenerada.

A seguir veremos vários exemplos de matrizes ortogonais para finalizar a compreensão do conceito de tudo.

Exemplo de matriz ortogonal 2×2

A seguinte matriz é uma matriz ortogonal de dimensão 2×2:

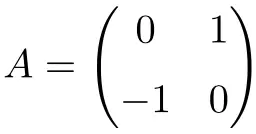
Podemos verificar que é ortogonal calculando o produto pela sua transposta:

$\displaystyle A\cdot A^t$

$\displaystyle A\cdot A^t= \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Como o resultado dá a matriz Idêntica, verificamos que A é uma matriz ortogonal.

Exemplo de matriz ortogonal 3×3

A seguinte matriz é uma matriz ortogonal de dimensão 3×3:

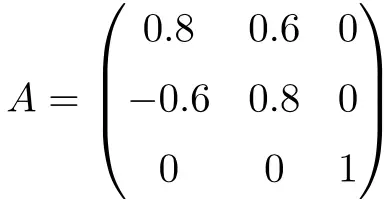
Podemos mostrar que é ortogonal multiplicando a matriz A pela sua transposta:

$\displaystyle A\cdot A^t = \begin{pmatrix}0.8&0.6&0\\[1.1ex] -0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}\cdot \begin{pmatrix}0.8&-0.6&0\\[1.1ex] 0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0\\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0&0&1\end{pmatrix}$

Como a solução é a matriz unitária, mostramos que A é uma matriz ortogonal.

Fórmula para encontrar uma matriz ortogonal 2×2

Veremos então a prova de que todas as matrizes ortogonais de ordem 2 seguem o mesmo padrão.

Considere uma matriz genérica de tamanho 2×2:

$\displaystyle A=\begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}$

Para que esta matriz seja ortogonal, a seguinte equação matricial deve ser satisfeita:

$\displaystyle A\cdot A^t =I$

$\displaystyle \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix} \cdot \begin{pmatrix} a & c \\[1.1ex] b & d \end{pmatrix} =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Resolvendo a multiplicação de matrizes, obtemos as seguintes equações:

$\displaystyle \begin{pmatrix} a^2+b^2 & ac+bd \\[1.1ex] ac+bd & c^2+d^2 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\displaystyle \begin{array}{c}a^2+b^2=1 \\[2ex] ac+bd=0 \\[2ex] c^2+d^2=1 \end{array} \qquad \begin{array}{l} (1) \\[2ex] (2) \\[2ex] (3) \end{array}$

Se você olhar de perto, essas igualdades se parecem muito com a relação trigonométrica pitagórica fundamental :

$\displaystyle \sin ^2\alpha+\cos ^2\alpha=1$

Consequentemente, os termos que satisfazem as equações (1) e (3) obtidas são:

$\displaystyle \begin{array}{l} a = \cos \theta \qquad \qquad \qquad c = \sin\phi \\[2ex] b = \sin \theta \qquad \qquad \qquad d = \cos \phi\end{array}$

Além disso, substituindo os valores na segunda equação, obtemos a relação entre os dois ângulos:

$\displaystyle ac+bd=0$

$\displaystyle \cos\theta\sin\phi+\sin\theta\cos\phi=0$

$\displaystyle \tan\phi=-\tan\theta$

Ou seja, uma das duas condições a seguir deve ser atendida:

$\displaystyle \text{si} \quad c=\sin\phi=-\sin\theta \quad \longrightarrow \quad d=\cos\phi=\cos\theta$

$\displaystyle \text{si} \quad d=\cos \phi=-\cos \theta \quad \longrightarrow \quad c=\sin\phi=\sin\theta$

Portanto, em conclusão, as matrizes ortogonais devem ter a estrutura de uma das duas matrizes a seguir:

fórmula para a matriz ortogonal de dimensão 2x2

Ouro

$\theta$

é um número real.

Com efeito, se a título de exemplo concedermos o valor

$\displaystyle\theta=\frac{\pi}{2}$

e pegarmos a primeira estrutura, obteremos a matriz que verificamos ser ortogonal na seção “Exemplo de matriz ortogonal 2×2”:

$\displaystyle M_1 \left(\theta =\frac{\pi}{2}\right)=\begin{pmatrix} \cos \cfrac{\pi}{2} &\sin \cfrac{\pi}{2} \\[4ex] -\sin \cfrac{\pi}{2} & \cos \cfrac{\pi}{2} \end{pmatrix}=\begin{pmatrix} \vphantom{\frac{\pi}{2}}0 &1 \\[2ex]\vphantom{\frac{\pi}{2}} -1 & 0 \end{pmatrix}$

Propriedades da Matriz Ortogonal

As características deste tipo de matriz são:

Uma matriz ortogonal nunca pode ser uma matriz singular , porque sempre pode ser invertida. Nesse sentido, a inversa de uma matriz ortogonal é outra matriz ortogonal.

Qualquer matriz ortogonal pode ser diagonalizada. Dizemos então que matrizes ortogonais são ortogonalmente diagonalizáveis.

Todos os autovalores ou autovalores de uma matriz ortogonal têm módulo igual a 1.

Qualquer matriz ortogonal composta apenas por números reais também é uma matriz normal.

O análogo da matriz ortogonal em um ambiente com números complexos é a matriz unitária.

Obviamente, a matriz identidade é uma matriz ortogonal.

O conjunto de matrizes ortogonais de dimensão n × n bem como a operação do produto matricial formam um grupo denominado grupo ortogonal. Ou seja, o produto de duas matrizes ortogonais é igual a outra matriz ortogonal.

Além disso, o resultado da multiplicação de uma matriz ortogonal pela sua transposta pode ser expresso pelo delta de Kronecker:

$\displaystyle (A\cdot A^{t})_{ij} = \delta_{ij}=\begin{cases}1 & \mbox{si }i = j, \\[2ex] 0 & \mbox{si }i \ne j\end{cases}$

Finalmente, o determinante de uma matriz ortogonal é sempre +1 ou -1.

$\displaystyle \text{det}(A)=\pm 1$

Exercício resolvido de matrizes ortogonais

Resolveremos então um exercício sobre matrizes ortogonais.

Dada a seguinte matriz quadrada de ordem 3, encontre os valores de
$a$

E

$b$

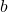
para torná-lo ortogonal:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix}$

Para que a ortogonalidade da matriz seja cumprida, o produto da matriz pela sua transposta deve ser igual à matriz Identidade. ENTÃO:

$\displaystyle A\cdot A^t = I$

$\displaystyle \frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix} \cdot \frac{1}{3}\begin{pmatrix}a&b&1\\[1.1ex] a&1&a\\[1.1ex] 1&b&a\end{pmatrix}=\begin{pmatrix}1&0&0\\[1.1ex] 0&1&0\\[1.1ex] 0&0&1\end{pmatrix}$

Multiplicamos as matrizes:

$\displaystyle \frac{1}{9}\begin{pmatrix}2a^2+1&ab+a+b&2a+a^2\\[1.5ex] ab+a+b&2b^2+1&b+a+ab\\[1.5ex] 2a+a^2&b+a+ab&1+2a^2\end{pmatrix} =\begin{pmatrix}1&0&0\\[1.5ex] 0&1&0\\[1.5ex] 0&0&1\end{pmatrix}$

Agora podemos obter uma equação do canto superior esquerdo das matrizes, porque os elementos nessa posição devem corresponder. Ainda:

$\displaystyle \frac{1}{9}(2a^2+1) = 1$

Resolvemos a equação e eliminamos a incógnita:

$\displaystyle 2a^2+1 = 9$

$\displaystyle 2a^2 = 8$

$\displaystyle a^2 = 4$

$\displaystyle \bm{a = \pm 2}$

No entanto, existem equações que não se sustentam com a solução positiva, por exemplo, aquela no canto superior direito. Portanto , apenas a solução negativa é possível .

Por outro lado, para calcular a variável

$b$

podemos combinar, por exemplo, os termos colocados na segunda linha da primeira coluna:

$\displaystyle \frac{1}{9}(ab+a+b) = 0$

$\displaystyle ab+a+b = 0$

Ao substituir o valor de

$a$

na equação:

$\displaystyle -2b-2+b = 0$

$\displaystyle -b =2$

$\displaystyle \bm{b =-2}$

Em suma, a única solução possível é:

$\displaystyle \bm{a=b =-2}$

Então a matriz ortogonal que corresponde a esses valores é:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}-2&-2&1\\[1.1ex] -2&1&-2\\[1.1ex] 1&-2&-2\end{pmatrix}$

Aplicações de matrizes ortogonais

Embora possa não parecer porque geralmente têm uma forma muito simples, as matrizes ortogonais são muito importantes na matemática, especialmente no campo da álgebra linear.

Na geometria, as matrizes ortogonais representam transformações isométricas (que não alteram distâncias e ângulos) em espaços vetoriais reais, por isso são chamadas de transformações ortogonais. Além disso, estas transformações são isomorfismos internos do espaço vetorial considerado. Estas transformações podem ser rotações , reflexões especulares ou inversões .

Por fim, esse tipo de matriz também é utilizado na física, pois permite estudar o movimento de corpos rígidos. E são até usados na formulação de certas teorias de campo.