Como fatorar polinômios (fatoração polinomial)

Nesta página explicamos como fatorar qualquer tipo de polinômio. Veremos primeiro como fatorar um polinômio com a regra de Ruffini, depois passaremos a como são fatorados polinômios sem termo independente, depois analisaremos as fatorações de polinômios raiz com frações e, por fim, os casos especiais de fatorações (notáveis identidades, fatoração por agrupamento, trinômios, etc.). Todas as explicações são feitas com exemplos e, além disso, ao final você poderá praticar com os exercícios resolvidos passo a passo para fatorar polinômios.

O que é fatoração polinomial?

A fatoração polinomial é uma técnica usada em matemática para decompor um polinômio no produto de fatores.

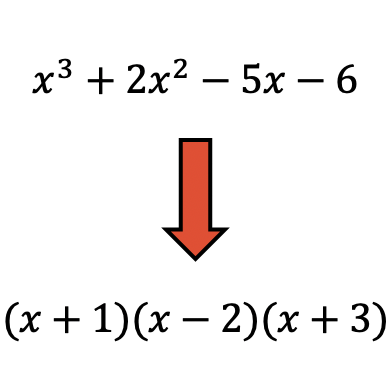
Fatorar polinômios é muito útil porque é mais fácil realizar operações com polinômios fatorados.

Agora que sabemos o que é fatoração polinomial, vamos ver como os polinômios são fatorados.

Como fatorar polinômios com a regra de Ruffini

Obviamente, para entender como fatorar um polinômio com a regra de Ruffini, primeiro você deve saber como aplicar a regra de Ruffini . Portanto, deixamos este link caso você queira primeiro revisar como era o procedimento.

Para fatorar um polinômio, as seguintes etapas devem ser seguidas:

1. As raízes do polinômio são calculadas de acordo com a regra de Ruffini.
2. Cada raiz encontrada do tipo x=a é expressa na forma de um fator (xa).
3. O polinômio fatorado é o produto de todos os fatores encontrados multiplicado pelo coeficiente do termo de maior grau do polinômio não ponderado.

Para que você veja como isso é feito e entenda melhor o procedimento de fatoração de polinômios, abaixo você encontrará um exemplo concreto explicado passo a passo:

• Fatore o seguinte polinômio:

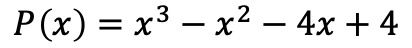
A primeira coisa a fazer é calcular as raízes ou zeros do polinômio. Para isso, precisamos encontrar os divisores do termo independente do polinômio , que neste caso são ±1, ±2 e ±4.

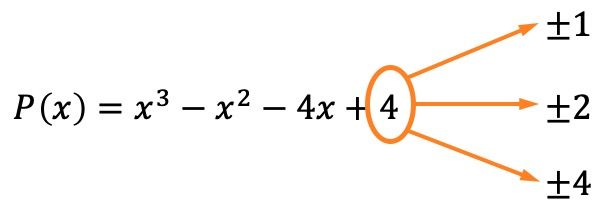
Agora sabemos, graças ao teorema do resto e dos fatores, que se o resto da divisão do polinômio por um desses valores for igual a 0, isso significa que esse valor é uma raiz do polinômio.

Devemos, portanto, dividir o polinômio por cada um dos divisores do termo independente com a regra de Ruffini e ver em quais casos o resto é zero.

Por exemplo, começamos aplicando a regra de Ruffini com

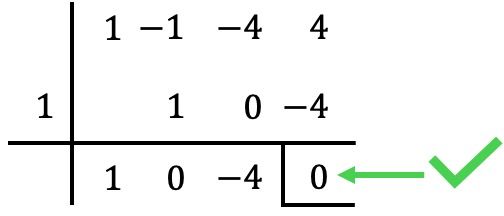
Neste caso, o resto (ou resíduo) da divisão é zero, então

É uma raiz do polinômio. ✅

Perfeito, já temos uma raiz do polinômio, só falta determinar as demais raízes restantes. Para fazer isso, usamos a regra de Ruffini com outro divisor do termo independente, por exemplo

Além disso, não há necessidade de usar o método de Ruffini com o polinômio inteiro, mas podemos continuar de onde paramos no passo anterior:

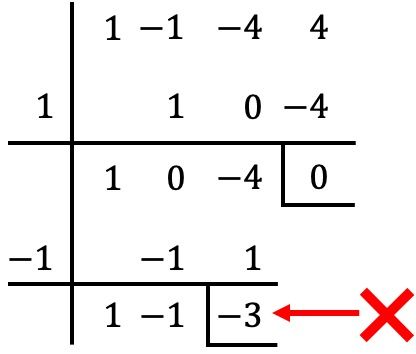
Porém, neste caso, ao dividir por

o resto obtido é diferente de 0, então

Não é uma raiz do polinômio. ❌

Devemos portanto tentar outro valor, por exemplo fazemos a regra de Ruffini com

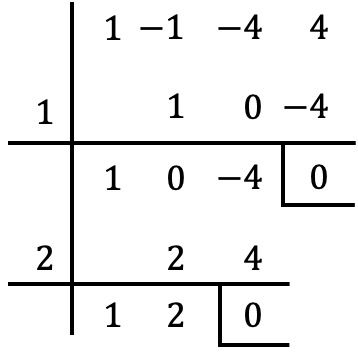
Neste caso, novamente obtemos um resto zero, então

É também uma raiz do polinômio.

E continuamos a aplicar o mesmo procedimento. Agora verificamos se

é uma raiz do polinômio ou não:

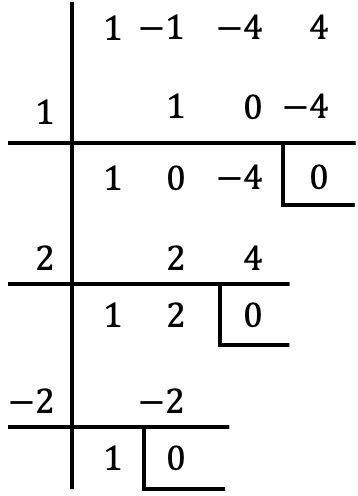
Ao dividir por

Com a regra de Ruffini obtemos resto zero, então

é uma raiz ou zero do polinômio.

Não podemos, portanto, continuar a aplicar a regra de Ruffini, pois já encontramos todas as raízes do polinômio, que são:

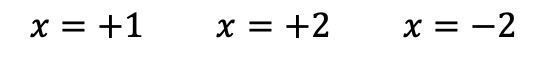
Depois de determinarmos todas as raízes do polinômio, podemos fatorá-lo. Para fazer isso, basta expressar cada raiz

na forma de um fator do tipo

, ou seja, para cada raiz você deve colocar um parêntese com um

e a raiz mudou de sinal:

E agora que temos todas as raízes expressas como fatores, devemos multiplicar todos os parênteses pelo coeficiente do termo de maior grau do polinômio original:

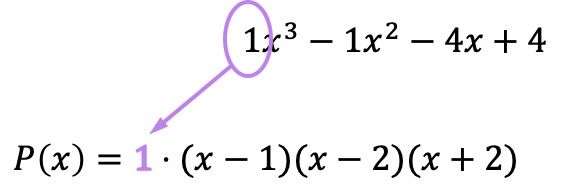
Embora neste caso o coeficiente seja 1 e, portanto, não afete o resultado, é importante lembrar de fazer esta multiplicação. Pois se o referido coeficiente fosse diferente de 1, o polinômio fatorado mudaria e, portanto, ao não inserir o número cometeríamos um erro na fatoração do polinômio.

Resumindo, o polinômio fatorado é:

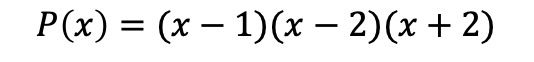
Fatoração de polinômios sem termo independente

Acabamos de ver que o termo independente é importante para a fatoração de polinômios, pois permite identificar as possíveis raízes do polinômio. No entanto, como fatorar um polinômio que não possui termo independente?

Para fatorar um polinômio sem termo independente , deve-se primeiro extrair o fator comum do polinômio, depois extrair as raízes do polinômio sem o fator comum usando a regra de Ruffini.

Escrito assim, pode parecer um pouco complicado, então vamos resolver um exemplo passo a passo para que você veja como fatorar um polinômio com um fator comum:

• Execute a decomposição fatorial do seguinte polinômio:

Como você pode ver, o polinômio do problema não possui um termo independente, então temos que pegar o fator comum do polinômio. Se olharmos atentamente, todos os elementos do polinômio têm pelo menos um

então o fator comum é

Portanto, ao extrair o fator comum do polinômio, obtemos a seguinte expressão:

E uma vez extraído o fator comum do polinômio, aplicamos a regra de Ruffini para calcular as raízes do polinômio agrupadas entre parênteses (com o procedimento que vimos na seção anterior):

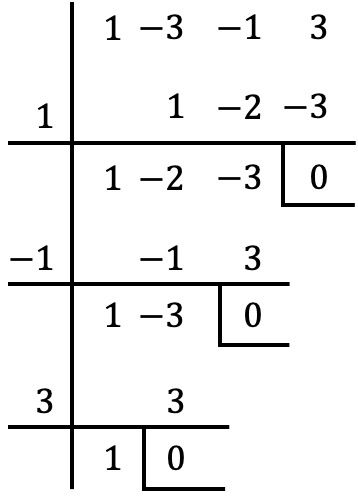
Portanto, as raízes ou zeros do polinômio entre parênteses são:

Portanto, para fatorar o polinômio, basta substituir o polinômio entre parênteses por suas raízes na forma fatorial (conforme explicado na seção acima):

E desta forma já fatoramos o polinômio que não tinha termo de grau 0. Observe que a única diferença é que primeiro temos que extrair um fator comum, mas todos os passos seguintes são exatamente iguais.

Por outro lado, você deve saber que

É também uma raiz do polinômio, pois quando extraímos o fator comum, implica que uma das raízes do polinômio é

Portanto, todas as raízes do polinômio são as seguintes:

Na verdade, o polinômio deve ter tantas raízes quanto o seu grau indicar. Neste caso o polinômio é de grau 4 e portanto possui 4 raízes.

Fatoração de polinômios com raízes racionais

Até aqui vimos exemplos de fatoração de polinômios com raízes inteiras, porém, um polinômio também pode ter raízes racionais, ou seja, com frações. Vamos ver como esse tipo de fatoração polinomial é resolvido com um exemplo:

• Fatore o seguinte polinômio incompleto:

Como sempre, utilizamos a regra de Ruffini com os divisores do termo independente para tentar determinar as raízes do polinômio:

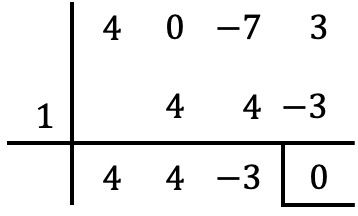
Mas não podemos calcular mais raízes com Ruffini, porque se tentarmos fazer Ruffini com todos os outros números divisores do termo independente obteremos um resto diferente de zero.

Encontramo-nos, portanto, numa situação em que só com

o restante da divisão equivale a 0, isso significa que o polinômio pode ter raízes fracionárias. Para determinar essas raízes poderíamos aplicar Ruffini com frações, porém é muito fácil cometer erros nos cálculos e é por isso que nestes casos costumamos fazer o seguinte:

Quando não podemos continuar aplicando a regra de Ruffini com raízes inteiras, devemos igualar o último polinômio obtido a 0 e resolver a equação resultante. Portanto, as raízes do polinômio serão os valores encontrados na equação.

Por outro lado, se a equação não tiver solução, isso significa que o polinômio não tem mais raízes e, portanto, não pode ser totalmente fatorado.

Portanto, definimos o polinômio quociente igual a zero:

E usamos a fórmula da equação quadrática para resolver a equação resultante:

As raízes do polinômio são, portanto:

O polinômio, portanto, tem raízes na forma de frações.

E uma vez que conhecemos todas as raízes do polinômio, podemos facilmente encontrar o polinômio fatorado expressando cada raiz

na forma de um fator do tipo

, ou seja, para cada raiz você deve colocar um parêntese com um

e a raiz mudou de sinal:

Lembre-se que para fatorar um polinômio, você também deve multiplicar seus fatores pelo coeficiente do termo de maior grau do polinômio não fatorado, que neste caso é 4.

Casos especiais de fatoração de polinômios

Normalmente, a regra de Ruffini (ou divisão sintética) é usada para fatorar um polinômio, conforme explicado acima. Mas dependendo do polinômio do problema, às vezes você pode fazer a fatoração polinomial mais rapidamente. Veremos cada um desses casos específicos a seguir.

Fatorando identidades notáveis

Se observarmos que um polinômio corresponde a uma identidade notável (ou a um produto notável) é muito simples fatorá-lo. Porém, para poder fazer isso você deve dominar as fórmulas para identidades notáveis , caso contrário recomendo que você dê uma olhada neste link onde você não só encontrará as fórmulas, mas também poderá ver exemplos de notáveis. identidades e você ainda pode praticar exercícios com elas resolvidas passo a passo.

Diferença de quadrados

Como você bem sabe, a fórmula para a identidade notável da diferença de quadrados é a seguinte:

Portanto, se encontrarmos um polinômio que satisfaça a expressão

podem ser levados em consideração diretamente.

Veja o seguinte exemplo em que uma diferença de quadrados é levada em consideração:

Por outro lado, as raízes do polinômio são:

Outros exemplos de fatoração de binômios que são diferenças de quadrados:

Quadrado de adição e subtração

Você já deve conhecer as fórmulas para as duas principais identidades notáveis restantes: o quadrado da adição e o quadrado da subtração.

Assim, se percebermos que um polinómio corresponde a uma destas duas identidades notáveis, podemos fatorá-lo diretamente. Veja os seguintes exemplos:

Identificar esses tipos de produtos notáveis é um pouco mais difícil. Um truque é verificar se o termo independente do polinômio é o quadrado de algum número e se o termo de grau superior é o quadrado de um monômio (geralmente

), neste caso basta verificar que é verdade que

é igual ao final do diploma intermediário.

Por exemplo, se tivermos o seguinte polinômio:

Neste caso, só pode ser o quadrado de uma soma, pois todos os elementos do polinômio são positivos. Então a variável

da fórmula deve ser 5, pois é a raiz do termo independente, e a variável

deve ser

, já que é a raiz do termo pode grau.

Tudo o que temos que fazer agora é provar que a fórmula do quadrado da soma se cumpre com o termo de grau intermediário:

✅

A fórmula para o produto notável é satisfeita, então o polinômio fatorado é:

E a raiz deste polinômio é

que é uma raiz dupla porque seu fator é elevado ao quadrado (é repetido duas vezes).

Abaixo estão mais exemplos de fatoração de trinômios quadrados perfeitos:

Fatoração de trinômios de segundo grau

Como acabamos de ver, às vezes existem trinômios que são quadrados perfeitos e podem ser fatorados diretamente com as fórmulas para identidades notáveis. Mas a maioria dos trinômios não são produtos notáveis, então como fatoramos esses casos de polinômios?

Para fatorar um polinômio quadrático não é necessário aplicar o método de Ruffini, basta igualar o polinômio a zero e resolver a equação quadrática resultante. As soluções da equação serão, portanto, as raízes do polinômio.

Por exemplo, se formos solicitados a fatorar o seguinte polinômio de grau 2:

Em vez de usar Ruffini, definimos o polinômio igual a 0:

E agora usamos a fórmula da equação do 2º grau para encontrar as soluções da equação:

As raízes do polinômio são, portanto:

E finalmente, a fatoração polinomial é:

Fatoração de trinômios de quarto grau com expoentes pares

Como no caso anterior, para fatorar um polinômio de quarto grau com expoentes pares, precisamos igualar o polinômio a zero e resolver a equação biquadrada. Para que os valores encontrados correspondam às raízes do polinômio.

Como exemplo, fatoraremos o seguinte polinômio de grau 4:

Primeiro, definimos o polinômio igual a zero:

Agora precisamos resolver a equação biquadrada. Para fazer isso, fazemos uma alteração de variável:

Resolvemos a equação quadrática com a fórmula:

Cancelamos a mudança de variável para calcular as raízes:

As raízes do polinômio são, portanto:

E uma vez que conhecemos as raízes ou zeros do polinômio, nós o fatoramos expressando suas raízes algebricamente na forma de fatores:

Fatoração de polinômios por agrupamento

Em alguns casos muito especiais, uma fórmula pode ser usada para fatorar um tipo muito particular de polinômio.

Se tivermos um polinômio da seguinte forma:

Podemos simplificar o polinômio removendo o fator comum:

E o polinômio pode ser ainda mais simplificado extraindo o fator comum uma segunda vez:

Desta forma conseguimos fatorar o polinômio sem aplicar Ruffini ou qualquer outro método. E as raízes desse polinômio seriam:

Agora vamos ver este método com um exemplo numérico:

Primeiro, removemos o fator comum com

e com 2:

E como agora

é um fator comum do polinômio, extraímos o fator comum de

As raízes do polinômio são, portanto:

Este método também é chamado de fatoração de polinômios por extração de fator comum duplo. Embora este seja um procedimento muito rápido, não recomendamos realizar este tipo de fatoração porque erros são frequentemente relatados ao fatorar com este método. Além disso, como vimos acima, um polinômio de grau 2 também pode ser fatorado resolvendo uma equação quadrática simples. Resumindo, nada acontece se você não entender bem esse método.

Por fim, deve-se notar que existem ainda outros métodos de fatoração polinomial mais complexos, como o algoritmo LLL, o método Kronecker e o método Trager, que não são explicados aqui devido à sua dificuldade matemática.

Exercícios resolvidos sobre fatoração de polinômios

Depois de ver todos os tipos de fatoração de polinômios, recomendamos que você pratique a tentativa de resolução de exercícios. É por isso que preparamos abaixo vários exercícios resolvidos passo a passo para fatoração de polinômios. Lembre-se que se você tiver alguma dúvida, pode escrevê-la nos comentários e responderemos rapidamente.

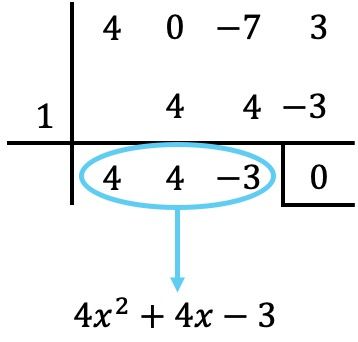
Exercício 1

Faça a fatoração do seguinte polinômio de grau 3:

É um polinômio completo, ordenado, de terceiro grau e, em última análise, independente. Portanto, aplicamos o método de Ruffini para determinar as raízes do polinômio:

As raízes do polinômio são, portanto, as seguintes:

A fatoração polinomial é, portanto:

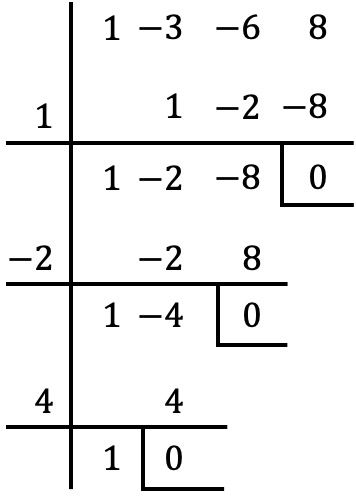
Exercício 2

Calcule a fatoração do seguinte polinômio de grau 4:

É um polinômio de quarto grau e com termo independente, portanto utilizamos o método de Ruffini para encontrar as raízes do polinômio:

As raízes do polinômio são, portanto:

E quando fatoramos o polinômio, ficamos com:

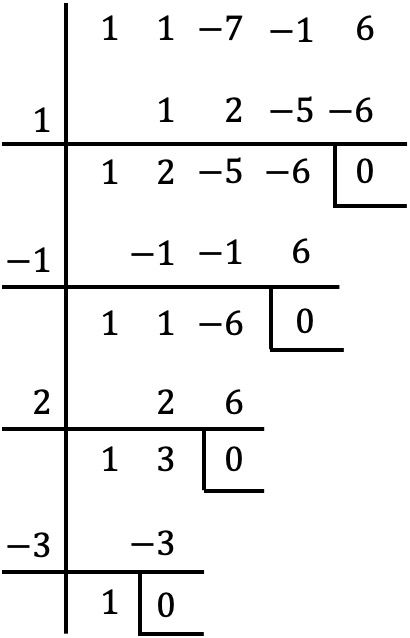
Exercício 3

Encontre a fatoração do seguinte polinômio de quarto grau:

Neste caso o polinômio não possui termo independente, devemos primeiro extrair um fator comum:

Agora que pegamos o fator comum de x, calculamos as raízes ou zeros do polinômio entre parênteses usando o método de Ruffini:

Assim as raízes do polinômio são aquelas que encontramos pelo método de Ruffini mais x=0 do fator comum:

E finalmente, decompondo o polinômio em fatores obtemos a seguinte expressão:

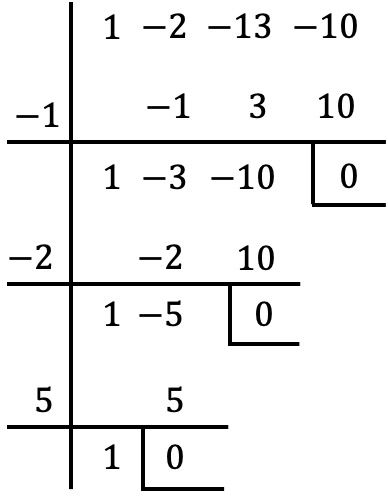
Exercício 4

Transforme o seguinte polinômio de terceiro grau em fatores:

Este polinômio possui um termo independente, portanto calculamos suas raízes com o algoritmo de Ruffini:

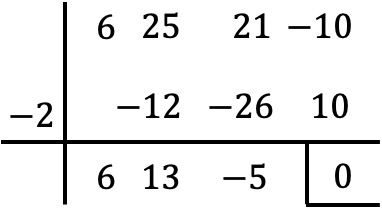
Porém, quando chegamos a este ponto, não podemos continuar a aplicar a regra de Ruffini, pois sem outro número inteiro o resto da divisão é zero.

Portanto, definimos o polinômio resultante igual a zero:

E aplicamos a fórmula das equações quadráticas para resolver a equação resultante:

As raízes ou zeros do polinômio são, portanto:

Portanto a fatoração do polinômio deve ser feita com frações:

Exercício 5

Determine a fatoração do seguinte polinômio de grau 6:

O polinômio do problema não possui termo independente, então devemos primeiro extrair o fator comum, que neste caso é

E uma vez removido o fator comum do polinômio, encontramos as raízes do polinômio entre parênteses usando a regra de Ruffini:

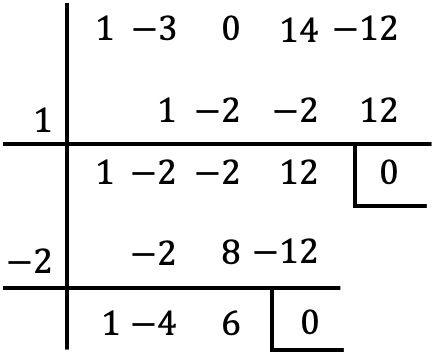
Mas quando chegamos a esta fase, não podemos continuar a avançar, porque sem outro número inteiro, o resto é zero.

Portanto, definimos o polinômio obtido igual a zero:

E resolvemos a equação quadrática com a fórmula:

Não existem raízes de números negativos, portanto a equação não tem solução, o que significa que não podemos encontrar mais raízes do polinômio. Em outras palavras, o polinômio não é completamente fatorável.

No entanto, as raízes que conseguimos encontrar são:

Observe que a raiz

é repetido duas vezes porque removemos o fator comum de

e como é elevado ao quadrado, isso implica que é uma raiz dupla.

Concluindo, o polinômio fatorado será o produto de todas as raízes encontradas expressas como fatores

multiplicado pelo polinômio obtido da regra de Ruffini que não pôde ser levado em consideração:

Exercício 6

Execute as fatorações de todos os seguintes polinômios:

O polinômio na seção A) corresponde a uma identidade notável, notadamente o quadrado da soma. Sua fatoração é portanto:

O polinômio da seção B) também é um produto notável, em particular é a diferença dos quadrados, portanto:

Da mesma forma, o polinômio na seção C) é uma igualdade notável, em particular consiste no quadrado de uma subtração. Sua fatoração é portanto:

Finalmente, o polinômio na parte D) não é uma identidade notável. Devemos, portanto, igualar o polinômio a 0 e resolver a equação resultante para encontrar suas raízes:

Usamos a fórmula da equação quadrática:

As raízes do polinômio D) são portanto:

E finalmente, o resultado da fatoração polinomial é: