Erro absoluto e erro relativo são duas medidas usadas para avaliar a precisão de um cálculo ou estimativa.
O erro absoluto refere-se à diferença entre o valor real e o valor estimado . Por sua vez, o erro relativo refere-se à razão entre o erro absoluto e o valor real.
Ambos são importantes porque fornecem informações sobre a precisão e relevância dos resultados. Além disso, eles são amplamente utilizados em muitos campos, incluindo engenharia, física e economia. Descrevemos cada um abaixo.
Qual é o erro absoluto?
O erro absoluto é uma medida da diferença entre um valor medido ou estimado e o valor real.
É representado pela fórmula: |valor medido – valor real| . Em outras palavras, o erro absoluto é o valor absoluto da diferença entre os valores medidos ou estimados e os valores reais.
Expresso em linguagem matemática, permanece o seguinte:
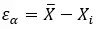
Vale ressaltar que é uma medida fundamental em diversas áreas, como ciência, tecnologia, engenharia e economia, pois permite avaliar a precisão dos resultados e a qualidade dos modelos e estimativas.
Como o erro absoluto é calculado?
Calcular o erro absoluto é simples:
O valor medido ou estimado é subtraído do valor real e o valor absoluto do resultado é obtido.
Por exemplo, se o valor real for 10 e o valor medido ou estimado for 9, o erro absoluto seria:
|9 – 10| = |-1| = 1.
Outro exemplo, se o valor real for 15 e o valor medido ou estimado for 17, o erro absoluto seria:
|17 – 15| = |2| = 2.
Você também pode calcular o erro médio absoluto , que é a soma total dos erros absolutos dividida pelo número de medições ou estimativas. Para calculá-lo, você deve seguir a seguinte fórmula:
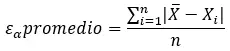
Isso é útil quando você tem muitas medições ou estimativas e deseja ter uma ideia geral da precisão dos resultados.
Suponha que tenhamos as seguintes medidas ou estimativas:
Valor atual: 20
Valor medido 1:18
Valor medido 2:22
Valor medido 3:19
Calculamos o erro absoluto para cada medição da seguinte forma:
Erro absoluto 1: |18 – 20| = 2
Erro absoluto 2: |22 – 20| = 2
Erro absoluto 3: |19 – 20| = 1
Calculamos o erro absoluto médio da seguinte forma: (2 + 2 + 1) ÷ 3 = 1,67. Isto indica que, em média, as medições ou estimativas estão dentro de 1,67 unidades do valor verdadeiro.
Qual é o erro relativo?
O erro relativo é uma medida da precisão de uma medição ou estimativa em termos da razão entre o erro absoluto e o valor verdadeiro.
É representado pela fórmula: (erro absoluto) ÷ (valor real) . Expresso em linguagem matemática, permanece o seguinte:
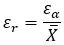
O erro relativo é útil para comparar a precisão de diferentes medições ou estimativas, especialmente quando os valores reais são diferentes.
Como o erro relativo é calculado?
Ao calcular o erro relativo, o erro absoluto é normalizado para que a precisão de diferentes medições ou estimativas possa ser comparada independentemente dos seus valores reais.
Por exemplo, suponha que você tenha duas medições ou estimativas, A e B, com valores verdadeiros de 10 e 100, respectivamente, e erros absolutos de 1 e 5, respectivamente.
O erro relativo para a medição A seria (1) ÷ (10) = (0,1), enquanto o erro relativo para a medição B seria (5) ÷ (100) = (0,05). Isto indica que a medição B é mais precisa do que a medição A em termos relativos, embora tenha um erro absoluto maior.
Aqui estão alguns exemplos de como o erro relativo pode ser calculado:
1. Meça a altura de um edifício e estima-se que seja de 100 metros:
Depois de fazer a medição, descobrimos que na verdade ele tem 98 metros de comprimento.
O erro absoluto seria de 2 metros e o erro relativo seria (2) ÷ (98) = 0,0204 ou 2,04%.
2. Suponha que você queira medir o peso de um objeto e estima que ele pesa 10 quilogramas.
Depois de fazer a medição, descobrimos que na verdade ele pesa 9,5 quilos.
O erro absoluto seria de 0,5 quilogramas e o erro relativo seria (0,5) ÷ (9,5) = 0,0526 ou 5,26%.
3. Suponha que você queira medir o comprimento de uma prancha e ele está estimado em 200 centímetros.
Depois de fazer a medição, descobrimos que na verdade são 201 centímetros.
O erro absoluto seria de 1 centímetro e o erro relativo seria (1) ÷ (201) = 0,00498 ou 0,498%.
Em cada um destes exemplos, o erro relativo fornece uma medida da precisão da medição em termos da razão entre o erro absoluto e o valor verdadeiro. Isso permite comparar a precisão de diferentes medições e estimativas, independentemente de seus valores reais.
Qual é a diferença entre erro absoluto e erro relativo?
Erro absoluto e erro relativo são duas medidas diferentes para avaliar a precisão de um resultado ou modelo.
Erro absoluto refere-se à diferença entre o valor real ou verdadeiro de uma quantidade e o valor estimado ou medido. Pode ser calculado como a diferença entre o valor real e o valor estimado:
Erro absoluto = valor real – valor estimado
O erro absoluto pode ser positivo ou negativo , dependendo se o valor estimado é maior ou menor que o valor verdadeiro.
Por outro lado, o erro relativo refere-se à relação entre o erro absoluto e o valor real ou verdadeiro . Pode ser calculado como a fração do erro absoluto e o valor verdadeiro:
Erro relativo = erro absoluto ÷ valor real
O erro relativo é normalmente expresso em percentagem . Este tipo de erro permite comparar a precisão de diferentes resultados ou modelos, independentemente da sua magnitude.
Por exemplo, um erro absoluto de 1,0 pode ser um desvio significativo de um valor pequeno, mas não de um valor grande. No entanto, o erro relativo em ambos os casos será o mesmo.
Em suma, o erro absoluto mede a diferença entre o valor real e o valor estimado, enquanto o erro relativo mede a precisão da estimativa em termos da sua relação com o valor real.
Quais são as aplicações do erro absoluto e do erro relativo?
O erro absoluto e o erro relativo têm uma ampla gama de aplicações em diferentes campos, incluindo:
- Ciência – Em experimentos científicos para avaliar a precisão das medições e a qualidade dos resultados.
- Tecnologia – Fabricação e controle de qualidade para avaliar a precisão de máquinas e equipamentos.
- Engenharia – Construção e projeto para avaliar a precisão das medições e garantir a qualidade dos produtos acabados.
- Economia : Avaliação de ativos e estimativa de risco financeiro para avaliar a precisão das projeções e tomar decisões informadas.
- Matemática e estatística : modelagem e estimativa para avaliar a precisão dos resultados e melhorar modelos.
Exemplos para calcular erro absoluto e erro relativo
Aqui estão dois exemplos simples para calcular o erro absoluto e o erro relativo:
1. Suponha que o peso de um objeto seja estimado em 3,0 kg e seu peso real seja 2,8 kg.
Calculamos o erro absoluto da seguinte forma:
Erro absoluto = Valor real – Valor estimado = 2,8 kg – 3,0 kg = -0,2 kg
Calculamos o erro relativo da seguinte forma:
Erro relativo = Erro absoluto ÷ Valor real = -0,2 kg ÷ 2,8 kg = -0,0714 ou -7,14%
2. Suponha que o volume de um recipiente seja estimado em 50 litros e que seu volume real seja de 45 litros.
Calculamos o erro absoluto da seguinte forma:
Erro absoluto = Valor real – Valor estimado = 45 litros – 50 litros = -5 litros
Calculamos o erro relativo da seguinte forma:
Erro relativo = Erro absoluto ÷ Valor real = -5 litros ÷ 45 litros = -0,1111 ou -11,11%
3. Suponha que a população de uma cidade seja estimada em 1 milhão de pessoas e que o número real seja de 975.000 pessoas.
Calculamos o erro absoluto da seguinte forma:
Erro absoluto = valor real – valor estimado = 975.000 – 1.000.000 = -25.000
Calculamos o erro relativo da seguinte forma:
Erro relativo = Erro absoluto ÷ Valor real = -25.000 ÷ 975.000 = -0,0257 ou -2,57%
4. Suponha que a área de um campo de futebol seja estimada em 10.000 metros quadrados e a área real seja de 9.900 metros quadrados.
Calculamos o erro absoluto da seguinte forma:
Erro absoluto = valor real – valor estimado = 9.900 – 10.000 = -100 metros quadrados
Calculamos o erro relativo da seguinte forma:
Erro relativo = Erro absoluto ÷ Valor real = -100 ÷ 9900 = -0,0101 ou -1,01%
Nestes exemplos, o erro absoluto e o erro relativo nos informam sobre a precisão da estimativa. O erro absoluto diz-nos o quanto a estimativa se desviou do valor verdadeiro, enquanto o erro relativo nos diz o quanto a estimativa se desviou em termos da sua relação com o valor verdadeiro.