Nesta página você encontrará as fórmulas para todas as equações do plano e como elas são calculadas. Você também descobrirá como encontrar a equação de qualquer plano com seu vetor normal. Além disso, você poderá ver exemplos e praticar com exercícios resolvidos das equações do plano.
Qual é a equação do plano?
Na geometria analítica, a equação de um plano é uma equação que permite que qualquer plano seja expresso matematicamente. Então, para encontrar a equação de um plano, você só precisa de um ponto e dois vetores linearmente independentes pertencentes a esse plano.
Antes de continuar com a explicação das equações planas, é fundamental que você entenda o que é plano (geometria) , pois caso contrário haverá coisas que você não entenderá. Caso não tenha ficado totalmente claro, você pode conferir neste link, onde concentramos tudo o que você precisa saber sobre o plano.
Quais são as equações do plano?
Como vimos na definição da equação de um plano, qualquer ponto de um plano pode ser expresso como uma combinação linear de 1 ponto e 2 vetores.

Porém, uma condição necessária para que a equação corresponda a um plano é que os dois vetores do plano tenham independência linear, ou seja, os dois vetores não podem ser paralelos entre si.
Assim, todos os tipos de equações do plano são: a equação vetorial , as equações paramétricas , a equação implícita (ou geral) e a equação canônica (ou segmental) do plano.
A seguir veremos detalhadamente a explicação e fórmula de todas as equações do plano.
Equação vetorial do plano
Considere um ponto e dois vetores de direção de um plano:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
A fórmula para a equação vetorial de um plano é:
![]()
Ou equivalente:
![]()
Ouro
![]()
E
![]()
são dois escalares, ou seja, dois números reais.
Equações paramétricas do plano
A equação paramétrica de um plano pode ser determinada a partir de sua equação vetorial. Abaixo você pode ver a demonstração.
Seja a equação vetorial de qualquer plano:
![]()
Operamos e primeiro realizamos os produtos dos vetores pelos escalares:
![]()
A seguir, adicionamos os componentes:
![]()
E, por fim, obtemos as equações paramétricas do plano assimilando as coordenadas correspondentes a cada variável separadamente:
![]()
Ouro:
-
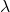
E
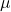
são dois escalares, ou seja, dois números reais.
-
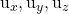
são os componentes de um dos dois vetores norteadores do plano
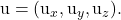
-
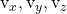
são os componentes do outro vetor diretor do plano
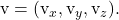
Equação implícita ou geral do plano
Considere um ponto e dois vetores de direção de um plano:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
A equação implícita, geral ou cartesiana de um plano é obtida resolvendo o seguinte determinante e igualando o resultado a 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
Assim, a equação implícita ou geral do plano resultante será a seguinte:
![]()
Este tipo de equação plana também é chamada de equação plana cartesiana.
Equação canônica ou segmentar do plano
A fórmula para a equação canônica ou segmentar de um plano é a seguinte:
![]()
Ouro:
-

é o ponto de intersecção entre o plano e o eixo X.
-

é o ponto de intersecção entre o plano e o eixo Y.
-

É aqui que o plano cruza o eixo Z.
A equação canônica (ou equação segmental) do plano também pode ser obtida a partir de sua equação geral:
![]()
Primeiro, resolvemos o coeficiente D da equação:
![]()
Em seguida, dividimos toda a equação do plano pelo valor do parâmetro D com sinal alterado:
![]()
![]()
E, utilizando as propriedades das frações, chegamos à seguinte expressão:
![]()
Deduzimos, portanto, desta expressão as fórmulas que permitem calcular diretamente os termos da equação canônica ou segmentar de um plano:
![]()
conseqüentemente, para poder formar esta variante das equações do plano, os coeficientes A, B e C devem ser diferentes de zero, evitando assim indeterminações das frações.
Como calcular a equação de um plano a partir de seu vetor normal
Um problema muito típico nas equações de um plano é descobrir como é a equação de um determinado plano, dado um ponto e seu vetor normal (ou perpendicular). Então, vamos ver como funciona.
Mas primeiro você deve saber que as componentes X, Y, Z do vetor normal a um plano coincidem respectivamente com os coeficientes A, B, C da equação implícita (ou geral) do referido plano.
![]()
Ouro
![]()
é o vetor ortogonal ao plano
![]()
Uma vez conhecida a relação anterior, vamos ver um exemplo de resolução deste tipo de problemas de equações planas:
- Determine a equação implícita ou geral do plano que passa pelo ponto
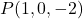
e um de seus vetores normais é
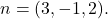
A fórmula para a equação implícita, geral ou cartesiana de um plano é:
![]()
Assim, a partir do vetor normal, podemos encontrar os coeficientes A, B e C porque são equivalentes às componentes do seu vetor normal:
![]()
Embora precisemos apenas encontrar o parâmetro D. Para isso, substituímos as coordenadas do ponto que pertence ao plano na equação:
![]()
![]()
![]()
![]()
![]()
Portanto, a equação implícita ou geral do plano é:
![]()
Problemas resolvidos de equações planas
Exercício 1
Determine a equação vetorial do plano que contém o vetor
![]()
e passa pelos dois pontos a seguir:
![]()
E
![]()
Para saber a equação de um plano são necessários um ponto e dois vetores e neste caso só temos um vetor, devemos portanto encontrar outro vetor diretor do plano. Para fazer isso, podemos calcular o vetor que define os dois pontos do plano:
![]()
Agora que já conhecemos dois vetores direções do plano e um ponto, usamos, portanto, a fórmula para a equação vetorial do plano:
![]()
E substituímos os dois vetores e um dos dois pontos do plano na equação:
![]()
Exercício 2
Encontre as equações paramétricas do plano que contém os três pontos a seguir:
![]()
Para encontrar as equações paramétricas do plano, precisamos encontrar dois vetores linearmente independentes que se ligam no plano. E, para isso, podemos calcular dois vetores que são definidos pelos 3 pontos:
![]()
![]()
As coordenadas dos dois vetores encontrados não são proporcionais, portanto são linearmente independentes um do outro.
Agora que já conhecemos dois vetores de direção e um ponto no plano, aplicamos a fórmula da equação paramétrica do plano:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
E substituímos os dois vetores e um dos três pontos do plano na equação:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f57edaf8a85108cffb796470ffca8484_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4cab5ddc074bd7df6849d71854207cf5_l3.png)
Exercício 3
Encontre a equação implícita ou geral do plano que passa pelo ponto
![]()
e contém os vetores
![]()
E
![]()
Para calcular a equação geral ou implícita do plano é necessário resolver o seguinte determinante formado pelos dois vetores, pelas três variáveis e pelas coordenadas do ponto:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
Então, substituímos os vetores e o ponto na fórmula:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-02e103601cd9992a8a8c087d016a08c1_l3.png)
E agora resolvemos o determinante da matriz 3×3 com o método de sua escolha:
![]()
Por fim, realizamos as operações e agrupamos termos semelhantes:
![]()
![]()
![]()
Portanto, a equação implícita ou geral do plano é:
![]()
Exercício 4
Determine se o ponto
![]()
pertence ao seguinte plano:
![]()
Para que o ponto esteja no plano, sua equação deve ser verificada. Portanto, precisamos substituir as coordenadas cartesianas do ponto na equação do plano e verificar se a equação é cumprida:
![]()
![]()
![]()
![]()
![]()
O ponto não respeita a equação do plano, portanto não faz parte deste plano.
Exercício 5
Encontre a equação segmental do plano cuja equação geral (ou implícita) é:
![]()
Primeiro, excluímos o termo independente da equação:
![]()
Em seguida, dividimos toda a equação do plano pelo valor do coeficiente D com sinal alterado:
![]()
![]()
E, utilizando as propriedades das frações, chegamos à seguinte expressão:
![]()
Portanto, a equação segmentar (ou canônica) do plano é:
![]()
Exercício 6
Calcula a equação implícita ou geral do plano no espaço que passa pelo ponto
![]()
e um de seus vetores normais é
![]()
A fórmula para a equação implícita, geral ou cartesiana de um plano é:
![]()
Bom, a partir do vetor normal podemos encontrar os coeficientes A, B e C, pois são respectivamente iguais às componentes do vetor normal:
![]()
Portanto, só precisamos encontrar o parâmetro D. Para isso, substituímos as coordenadas do ponto que pertence ao plano na equação:
![]()
![]()
![]()
![]()
![]()
Concluindo, a equação implícita ou geral do plano é:
![]()
Exercício 7
Encontre as equações paramétricas do plano que contém a reta
![]()
e é paralelo à direita
![]()
sendo as linhas:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-624f315685b292c4bb05e9cb4b931a97_l3.png)
Para encontrar as equações paramétricas do plano, precisamos conhecer dois vetores diretores e um ponto no plano. A declaração nos diz que contém a linha
![]()
Portanto, podemos pegar o vetor direção e um ponto nesta reta para definir o plano. Além disso, a afirmação nos diz que o plano é paralelo à linha
![]()
então também podemos usar o vetor diretor desta reta para a equação do plano.
o certo
![]()
é expresso na forma de equações paramétricas, então os componentes de seu vetor de direção são os coeficientes dos termos dos parâmetros
![]()
![]()
E as coordenadas cartesianas de um ponto nesta mesma reta são os termos independentes das equações paramétricas:
![]()
Por outro lado, a linha reta
![]()
está na forma de uma equação contínua, tal que os componentes de seu vetor de direção são os denominadores das frações:
![]()
Portanto, as equações paramétricas do plano são:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c81f4d8e5aa907f111b3389d5137736e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fccd86ac9a3e4084e324d8e5b1071e59_l3.png)