Equações paramétricas do plano

Nesta página você encontrará o que são as equações paramétricas de um plano e como são calculadas (fórmula). Além disso, você poderá ver exemplos e praticar com exercícios resolvidos passo a passo.

Quais são as equações paramétricas de um plano?

Na geometria analítica, as equações paramétricas de um plano são equações que permitem que qualquer plano seja expresso matematicamente. Para encontrar as equações paramétricas de um plano, precisamos apenas de um ponto e de dois vetores linearmente independentes pertencentes a esse plano.

Formulação de equações paramétricas do plano

Considere um ponto e dois vetores de direção de um plano:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

A fórmula para as equações paramétricas de um plano é:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Ouro

$\lambda$

$\mu$

são dois escalares, ou seja, dois números reais.

É importante que os dois vetores de direção da equação plana sejam linearmente independentes, ou seja, tenham direção diferente (não paralela). Caso contrário, a equação acima não representaria nenhum plano.

Por outro lado, tenha em mente que além da equação paramétrica, existem outras formas de expressar analiticamente um plano no espaço (em R3), como a equação geral do plano . Neste link você encontrará sua fórmula, como é calculada a partir das equações paramétricas do plano, exemplos e exercícios resolvidos.

Exemplo de como encontrar equações paramétricas de um plano

Depois de vermos o que é a equação paramétrica do plano, vamos ver como ela é calculada usando um exemplo:

Encontre as equações paramétricas do plano que passa pelo ponto
$P(1,3,2)$

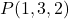
e contém os vetores

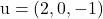
$\vv{\text{u}}=(2,0,-1)$

E

$\vv{\text{v}}=(4,2,3)$

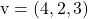
Para determinar as equações paramétricas do plano, basta aplicar sua fórmula:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

E agora substituímos o ponto e cada vetor de direção na equação:

$\displaystyle \begin{cases}x=1 + \lambda \cdot 2 + \mu \cdot 4 \\[1.7ex] y=3+ \lambda \cdot 0 + \mu \cdot 2\\[1.7ex] z=2 + \lambda\cdot (-1)+ \mu \cdot 3\end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + 2\lambda + 4\mu } \\[1.7ex] \bm{y=3 + 2\mu}\\[1.7ex] \bm{z=2 -\lambda+ 3\mu} \end{cases}$

Como passar da equação vetorial de um plano para equações paramétricas

Outro método para determinar as equações paramétricas de um plano é a partir da equação vetorial de um plano. Abaixo você pode ver a demonstração.

Seja a equação vetorial de qualquer plano:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Operamos e primeiro realizamos os produtos dos vetores pelos escalares:

$(x,y,z)=(P_x,P_y,P_z)+ (\lambda\text{u}_x,\lambda\text{u}_y,\lambda\text{u}_z) +(\mu\text{v}_x,\mu\text{v}_y,\mu\text{v}_z)$

A seguir, adicionamos os componentes:

$(x,y,z)=(P_x+\lambda \text{u}_x + \mu \text{v}_x,P_y+\lambda \text{u}_y + \mu \text{v}_y,P_z+\lambda \text{u}_z + \mu \text{v}_z)$

E, por fim, obtemos a equação paramétrica do plano assimilando as coordenadas correspondentes a cada variável separadamente:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Como você pode ver nos dois exemplos acima, encontrar as equações paramétricas de um plano é relativamente fácil. Porém, os problemas podem ficar um pouco complicados, então abaixo você tem vários exercícios resolvidos de diferentes dificuldades para você praticar.

Problemas resolvidos de equações paramétricas do plano

Exercício 1

Determine as equações paramétricas do plano que contém o vetor

$\vv{\text{u}}=(2,1,5)$

e passa pelos dois pontos a seguir:

$A(3,2,-1)$

$B(-2,-1,1).$

veja solução

Para saber a equação de um plano são necessários um ponto e dois vetores e neste caso só temos um vetor, devemos portanto encontrar outro vetor diretor do plano. Para fazer isso, podemos calcular o vetor que define os dois pontos do plano:

$\vv{AB} = B - A = (-2,-1,1) - (3,2,-1) = (-5,-3,2)$

Agora que já conhecemos dois vetores direções do plano e um ponto, usamos, portanto, a fórmula para as equações paramétricas do plano:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

E substituímos os dois vetores e um dos dois pontos do plano na equação:

$\displaystyle \begin{cases}x=3 + \lambda \cdot 2+ \mu \cdot (-5) \\[1.7ex] y=2 + \lambda \cdot 1 + \mu \cdot (-3) \\[1.7ex] z=(-1) + \lambda\cdot 5 + \mu \cdot 2 \end{cases}$

$\displaystyle \begin{cases}\bm{x=3 +2 \lambda-5\mu } \\[1.7ex] \bm{y=2 + \lambda-3 \mu } \\[1.7ex] \bm{z=-1 + 5\lambda + 2\mu } \end{cases}$

Exercício 2

Encontre as equações paramétricas do plano que contém os três pontos a seguir:

$A(4,1,0) \qquad B(2,-3,-1) \qquad C(1,5,3)$

veja solução

Para encontrar as equações paramétricas do plano, precisamos encontrar dois vetores linearmente independentes que se ligam no plano. E, para isso, podemos calcular dois vetores que são definidos pelos 3 pontos:

$\vv{AB} = B - A = (2,-3,-1) - (4,1,0) = (-2,-4,-1)$

$\vv{AC} = C - A = (1,5,3) - (4,1,0) = (-3,4,3)$

As coordenadas dos dois vetores encontrados não são proporcionais, portanto são linearmente independentes um do outro.

Agora que já conhecemos dois vetores de direção e um ponto no plano, aplicamos a fórmula da equação paramétrica do plano:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

E substituímos os dois vetores e um dos três pontos do plano na equação:

$\displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}$

$\displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}$

Exercício 3

Calcule as equações paramétricas do plano definido pela seguinte equação vetorial:

$(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)$

veja solução

Para transformar a equação vetorial do plano em uma equação paramétrica, você deve operar com as coordenadas e depois resolver cada variável separadamente:

$(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)$

$(x,y,z)=(0,-1,5)+(6\lambda,\lambda,-2\lambda) + (\mu,-\mu,3\mu)$

$(x,y,z)=(6\lambda+\mu,-1+\lambda-\mu,5-2\lambda+3\mu)$

$\displaystyle \begin{cases}\bm{x=6\lambda+\mu } \\[1.7ex] \bm{y=-1+\lambda-\mu} \\[1.7ex] \bm{z=5-2\lambda+3\mu } \end{cases}$

Exercício 4

Encontre as equações paramétricas do plano que contém a reta

$r$

e é paralelo à direita

$s.$

sendo as linhas:

$\displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}$

veja solução

Para encontrar as equações paramétricas do plano, precisamos conhecer dois vetores diretores e um ponto no plano. A instrução nos diz que contém a linha

$r$

Portanto, podemos pegar o vetor direção e um ponto nesta reta para definir o plano. Além disso, a afirmação nos diz que o plano é paralelo à linha

$s,$

então também podemos usar o vetor diretor desta reta para a equação do plano.

o certo

$r$

é expresso na forma de equações paramétricas, então os componentes de seu vetor de direção são os coeficientes dos termos dos parâmetros

$t:$

$\vv{r} =(1,-3,2)$

E as coordenadas cartesianas de um ponto nesta mesma reta são os termos independentes das equações paramétricas:

$P(1,2,4)$

Por outro lado, a linha reta

$s$

está na forma de uma equação contínua, tal que os componentes de seu vetor de direção são os denominadores das frações:

$\vv{s} =(2,2,-3)$

Portanto, as equações paramétricas do plano são:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

$\displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}$

Quais são as equações paramétricas de um plano?

Formulação de equações paramétricas do plano

Exemplo de como encontrar equações paramétricas de um plano

Como passar da equação vetorial de um plano para equações paramétricas

Problemas resolvidos de equações paramétricas do plano

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Deixe um comentário Cancelar resposta