Equações de primeiro grau ou equações lineares são a base da álgebra , porque se você não as entender, será muito difícil entender equações mais complexas. Portanto, a particularidade deste tipo de equações é que a parte literal dos monômios não pode ter expoente. Portanto, em uma equação linear encontraremos apenas monômios sem parte literal e monômios com parte literal sem expoente, como por exemplo: 3 + x = -5 – 3x .
Observe também que essas equações geralmente têm uma solução única, embora possam não ter. Para saber qual caso temos diante de nós, devemos resolver a equação e no final analisar o resultado . Portanto, se obtivermos uma igualdade impossível como 2 = 0, a equação não terá solução. Por outro lado, se obtivermos uma igualdade sempre verdadeira, então a solução será equivalente a todos os números reais. E por último, se ao final obtivermos a igualdade de X e um valor numérico, neste caso teremos um resultado único.
Procedimento para resolver uma equação linear
Resolver uma equação equivale a calcular o valor de uma variável, representada por uma letra (x, y, a, b…). Então, para encontrar esse valor precisamos seguir os seguintes passos:
- Resolva parênteses e frações: Para começar, removemos todos os parênteses e denominadores, para obter uma equação mais fácil de entender. Como podemos apreciar diretamente quais termos são acompanhados pelo desconhecido e quais não são, esta leitura permite-nos continuar facilmente a resolver a expressão.
- Vamos simplificar a expressão: agrupamos termos semelhantes (termos independentes por um lado, e termos com x por outro). Então, de um lado deixaremos os números que possuem a incógnita e passaremos os demais números para o lado oposto. Mas lembre-se, para mudar os seus lados, temos que mudar o seu sinal.
- Operar em cada lado: Realizamos todas as operações na seguinte ordem: potências/raízes, multiplicações/divisões e adições/subtrações. Fazemos isso até obtermos um único termo de cada lado, e assim terminamos com uma equação com a mesma estrutura que esta: 4x = 8.
- Isole a variável: por fim, basta passar o valor que acompanha a letra dividindo do outro lado e assim encontramos o seu valor final. Ao final desta etapa teremos resolvido a incógnita e saberemos que tipo de resultado resta: uma solução única, uma solução inválida ou uma solução satisfeita com todos os inteiros.
Exemplos de equações de primeiro grau
Abaixo você encontrará equações de primeiro grau resolvidas , que são organizadas em diferentes categorias de acordo com a complexidade de sua estrutura. Assim, conhecendo o procedimento teórico para resolver equações lineares e os diferentes tipos que existem, você já terá o conhecimento necessário para poder resolvê-las facilmente e começaremos pela prática. Dito isto, vamos começar com a explicação teórica:
Equações básicas de primeiro grau
Este primeiro tipo de equações lineares consiste apenas em operações aritméticas básicas (adição, subtração, multiplicação e divisão). Aqui estão dois exemplos trabalhados, o primeiro é um pouco mais básico e o segundo é um pouco mais complexo em termos de cálculo:
-6x + 4 – 1 = 6x -3
-6x + 3 = 6x – 3
-6x – 6x = -3 – 3
-12x = -6
x = 1 / 2
-24x – 3 + 4x = -4x – 27
-20x – 3 = -4x – 27
-20x + 4x = -27 + 3
-16x = -24
x = 3/2
Equações de primeiro grau com parênteses
Em segundo lugar, temos as equações lineares entre parênteses. Estes são um pouco mais complicados de resolver que os anteriores, embora a única dificuldade esteja no cálculo, pois as propriedades dos parênteses devem ser respeitadas. Para deixar mais claro, mostramos dois exemplos práticos:
2(x + 3) – 4x = -4
2x + 6 – 4x = -4
-2x = -10
x = 5
-2 + 3 (4x + 5) = -1 (x + 2) + 2 (-3x + 2)
-2 + 12x + 15 = -x – 2 – 6x + 4
13 + 12x = -7x + 2
12x + 7x = -13 + 2
19x = -11
x = -11/19
Equações de primeiro grau com potências e raízes
O terceiro nível é bastante simples, pois apenas acrescenta poderes e raízes. A única dificuldade que você pode encontrar com essas equações é quando o expoente ou raiz afeta um parêntese inteiro (como no segundo exemplo que mostraremos), mas todo o resto permanece praticamente o mesmo. Abaixo estão dois exemplos.
3² + √25 – 2x = 2³x + 4
9 + 5 – 2x = 8x + 4
14 – 2x = 8x + 4
-2x – 8x = -14 + 4
-10x = -10
x = 1
4x + (2 – 1 +5)² = 3x – √16
4x + 6² = 3x – 4
4x – 3x = -4 -36
x = -40
Equações de primeiro grau com frações
A última categoria de equações lineares que podemos encontrar é esta, que é composta por todos os elementos que comentamos anteriormente e também por frações. Este nível é o mais complexo e existem vários métodos para resolvê-los. A primeira e mais simples é multiplicar os denominadores pelo lado oposto da igualdade, embora só possamos utilizar isto quando tivermos duas frações. Por outro lado, se tivermos mais de duas frações na equação, devemos encontrar um denominador comum e multiplicar todas as frações dividindo esse valor pelo denominador da mesma fração. Abaixo está um exemplo de cada tipo:
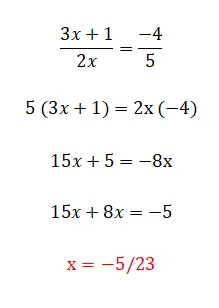
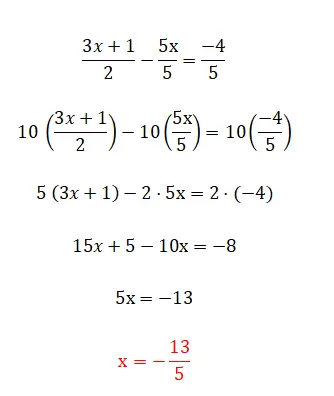
Exercícios sobre equações de primeiro grau
Agora oferecemos alguns exercícios de equações lineares. Elas são organizadas de acordo com a dificuldade crescente, sendo as primeiras equações mais fáceis que as últimas. Portanto, recomendamos que você comece do início e veja até onde consegue ir. Portanto, tente resolver as equações a seguir e compare seu resultado com as soluções que fornecemos.
Primeiro exercício
O primeiro exercício é uma equação linear muito simples, pois consiste apenas em adições e subtrações, e também possui apenas quatro termos entre os dois lados da igualdade:
2x – 3 = 4x + 5
2x – 4x = 5 + 3
-2x = 8
x = 8 / (-2)
x = -4
- Agrupamos termos semelhantes.
- Simplificamos ambos os lados.
- Apagamos o desconhecido e calculamos seu valor.
segundo exercício
Neste caso, nos encontramos com uma equação formada por parênteses, com a qual nossa prioridade é eliminá-los, para podermos então agrupar termos semelhantes:
-4(x + 2) + 5x = 6 + 5x
-4x – 8 + 5x = 6 + 5x
-4x + 5x – 5x = 6 + 8
-4x = 14
x = 14 / (-4) = -7/2
- Resolvemos os parênteses.
- Movemos os x para a esquerda e os termos independentes para a direita.
- Esclarecemos o desconhecido.
Simplificamos o resultado.
terceiro exercício
A seguir, você precisará resolver outra equação quadrática entre parênteses, embora esta seja um pouco mais difícil. Isso ocorre porque ele possui parênteses aninhados (parênteses dentro de outros parênteses). Portanto, você deve seguir corretamente a ordem de resolução: primeiro os internos e depois os externos.
3x + 2 (x – (4x – 5)) = 1 – (3 (2x + 7) – 2)
3x + 2 (x – 4x + 5) = 1 – (6x + 21 – 2)
3x + 2x – 8x + 10 = 1 – 6x – 21 + 2
-3x + 10 = -6x – 18
3x = -28
x = -28/3
- Começamos resolvendo os parênteses internos.
- A seguir, resolvemos os parênteses externos.
- Simplificamos ambos os lados da igualdade e coletamos termos semelhantes.
- Isolamos x e calculamos seu valor.
quarto exercício
Neste exercício começamos a ver as frações, que são provavelmente o elemento mais complicado das equações lineares. Mas não se preocupe porque se você leu a teoria saberá perfeitamente como fazê-lo:
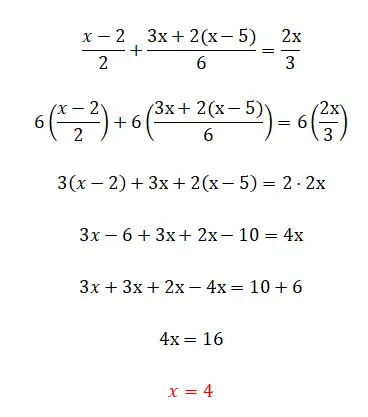
Quinto exercício
Neste quinto exercício, vemos frações entre parênteses, o que significa que a hierarquia de resolução fica um pouco complicada. Vale ressaltar que este exemplo pode ser resolvido através de dois métodos: utilizando o método dos mínimos múltiplos comuns ou operando diretamente com frações. Abaixo você confere os dois procedimentos completos:
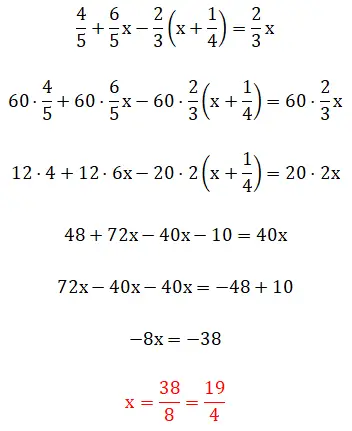
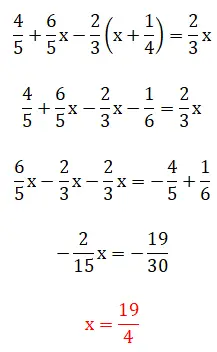
sexto exercício
A seguir, vamos um pouco mais longe no tópico de frações e parênteses, já que temos parênteses aninhados. Este exercício não traz muito mais complicações em relação ao anterior, é simplesmente um pouco mais difícil em termos de cálculos e pronto.
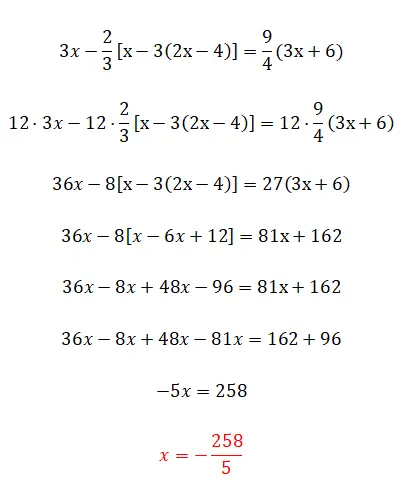
- Multiplicamos todos os termos pelo lcmp dos denominadores.
- Simplificamos a expressão removendo os parênteses: primeiro os que estão dentro e depois os que estão fora.
- Agrupamos termos semelhantes em cada lado.
- Resolvemos as operações de cada lado.
- E calculamos o valor da incógnita.
sétimo exercício
O exercício a seguir pode parecer muito fácil, mas recomendamos que você tente resolvê-lo mesmo assim, pois certamente lhe dará um resultado um tanto incomum. Depois de tentar, veja a solução e a explicação abaixo do exercício.
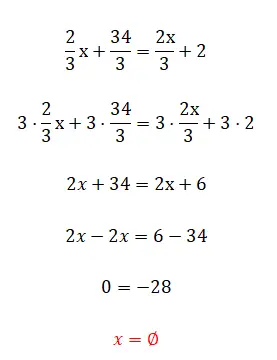
- Multiplicamos todas as frações pelo lcm dos denominadores.
- Simplificamos a expressão obtida.
- E finalmente vemos que isso nos dá uma falsa igualdade, uma vez que eliminamos o desconhecido.
Como você deve ter notado, esta é uma falsa igualdade ou uma igualdade sem resultado, pois não existe nenhum valor que complete corretamente a equação. Este é um dos casos que mencionamos na introdução.
oitavo exercício
Por último, oferecemos-lhe este exercício que é bastante complicado porque tem todas as complicações que vimos ao longo deste artigo, embora também tenha um pequeno truque. Comente que se você conseguiu resolver esta equação de primeiro grau, então você entendeu toda a teoria perfeitamente. E se não, não se preocupe, pois este exercício é bastante complicado.
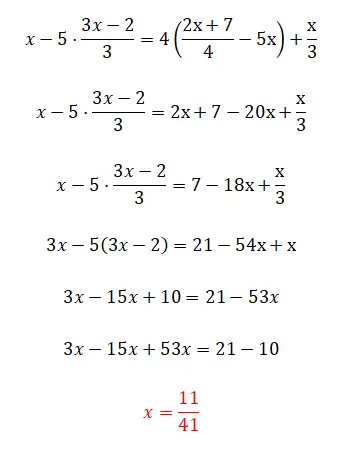
- Começamos eliminando os quatro do lado direito da equação.
- Então juntamos os x do lado direito.
- Multiplicamos todos os termos por três, para eliminar os denominadores.
- Removemos os parênteses.
- Juntamos termos semelhantes.
- Calculamos o valor da incógnita.
Mais exercícios de equações lineares
Agora que você já praticou o suficiente, deverá ser capaz de resolver equações lineares complexas . Porém, se você quiser continuar praticando, recomendamos que tente resolver esta planilha . Mas se você acha que já cobriu o suficiente, também podemos oferecer um artigo que pode ajudá-lo a entender a hierarquia das operações . Assim você saberá qual cálculo resolver primeiro em todos os momentos e nunca cometerá erros .