Equação da reta tangente -

Neste artigo veremos como encontrar a equação da tangente a uma curva. Além disso, você pode treinar com exercícios resolvidos de diferentes níveis de dificuldade.

Equação da reta tangente a uma função em um ponto

A equação da tangente à função f(x) no ponto x=x ₀ é:

$y -y_0= m(x-x_0)$

Onde o ponto P(x ₀ ,y ₀ ) é o ponto onde a tangente e a função coincidem. E a inclinação da tangente, m, é igual à derivada da curva no ponto x ₀ , ou seja, m=f'(x ₀ ).

Na imagem acima você pode ver uma curva

$f(x)$

representado em azul e uma linha laranja tangente à função

$f(x)$

Sobre

$x=x_0$

, já que eles só têm esse ponto em comum. Bem, a equação desta tangente é

$y -y_0= m(x-x_0)$

, e sua inclinação é

$m=f'(x_0)$

Como encontrar a equação tangente

Para encontrar a equação da tangente a uma função em um ponto, você precisa fazer:

Encontre a inclinação da reta tangente calculando a derivada da função no ponto de tangência.
Determine um ponto na reta tangente.
Encontre a equação da reta tangente usando a inclinação calculada e o ponto da reta tangente.

Exemplo da equação da tangente a uma curva

Depois de vermos a teoria da equação tangente, vamos ver como calcular a equação de uma tangente resolvendo um exemplo passo a passo:

Calcule a equação da tangente à curva
$f(x)=x^2+x$

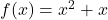
Sobre

$x=1$

.

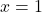
Sabemos que a equação tangente tem sempre a seguinte forma:

$y -y_0= m(x-x_0)$

A primeira coisa a fazer é calcular a inclinação da linha. Assim, a inclinação da tangente,

$m$

, será o valor da derivada da curva no ponto de tangência x=1, ou seja

$m=f'(1).$

Portanto, diferenciamos a função e calculamos

$f'(1):$

$f(x)=x^2+x \quad \longrightarrow \quad f'(x)=2x+1$

$f'(1)= 2\cdot 1+1=2+1=3$

$m=f'(1)=3$

Uma vez que sabemos o valor de

$m$

, precisamos encontrar um ponto

$(x_0,y_0)$

da reta tangente para completar a equação da reta tangente.

A equação da tangente e da curva sempre tem um ponto comum , que neste caso é

$x=1$

. Portanto, como a curva

$f(x)$

passa por este ponto, podemos encontrar a outra componente do ponto calculando

$f(1):$

$f(x)=x^2+x$

$f(1)=1^2+1=2$

O ponto de tangência é portanto:

$P(1,2)$

Tanto a curva como a tangente passam por este ponto, portanto também podemos utilizá-lo para determinar a equação da tangente.

Resta substituir os valores encontrados da inclinação e do ponto da tangente em sua equação:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=3 \qquad P(1,2) \end{array} \right\} \longrightarrow \ y -2= 3(x-1)$

Resumindo, a equação tangente é:

$\bm{y-2=3(x-1)}$

Você também pode expressar a equação da reta tangente com a equação explícita da reta:

$\bm{y=3x-1}$

Abaixo você pode ver a curva representada

$f(x)=x^2+x$

e sua reta tangente a

$x=1,$

$y-2=3(x-1):$

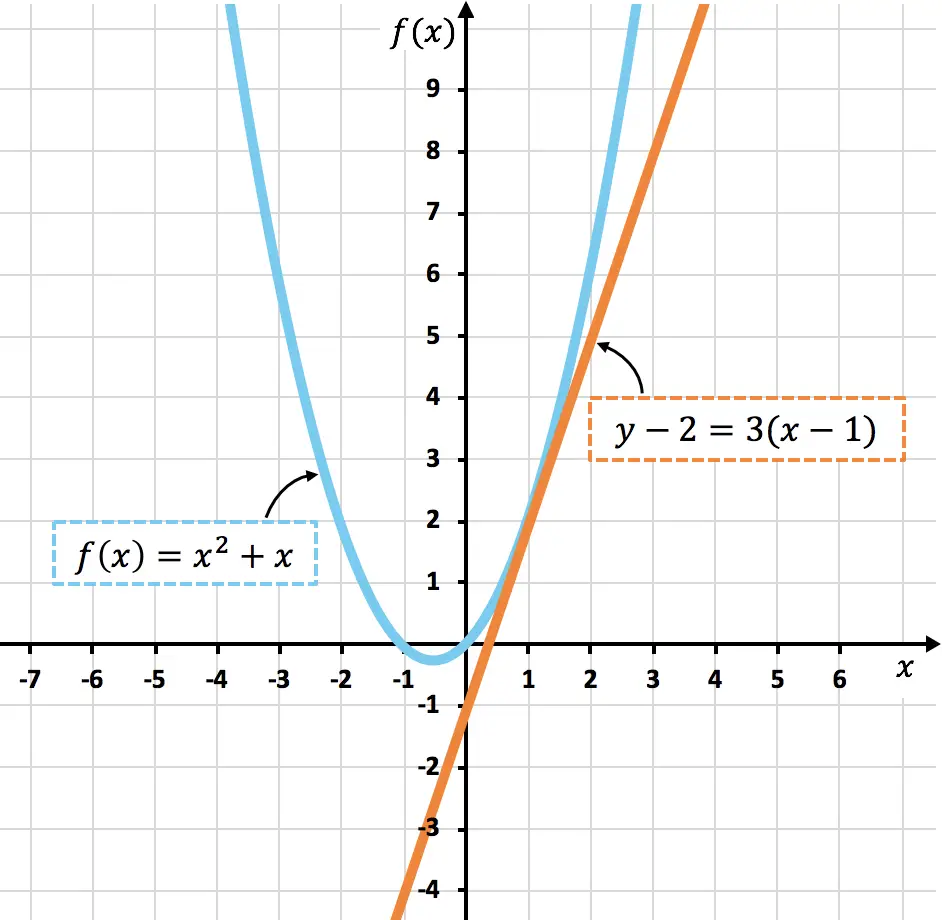
equação da reta tangente a uma curva em um ponto

Como você pode ver, a curva

$f(x)=x^2+x$

e a tangente

$y-2=3(x-1)$

eles só têm em comum o ponto

$(1,2)$

, exatamente como calculamos.

Exercícios resolvidos sobre a equação tangente

Exercício 1

Calcule a equação da tangente à curva

$f(x)=2x^2-4x+3$

Sobre

$x=2 .$

Veja a solução

A equação tangente sempre terá a seguinte forma:

$y-y_0=m(x-x_0)$

Passo 1: Calcule a inclinação da linha tangente

A inclinação, m , é o valor da derivada da curva no ponto de tangência. Portanto, neste caso

$m = f'(2):$

$f(x)=2x^2-4x+3 \ \longrightarrow \ f'(x)= 4x-4$

$f'(2)= 4\cdot 2-4=8-4=4$

$m=f'(2)=4$

Passo 2: Encontre um ponto na linha tangente

A equação da tangente e da curva sempre tem um ponto comum, que neste caso é

$x=2$

. Portanto, como a curva

$f(x)$

passa por este ponto, podemos encontrar a outra componente do ponto calculando

$f(2):$

$f(x)=2x^2-4x+3$

$f(2)=2\cdot 2^2-4\cdot 2+3 =2 \cdot 4 -8 +3 = 3$

Assim, o ponto pelo qual passam a curva e a tangente é o ponto

$(2,3).$

Etapa 3: Escreva a equação tangente

Resta substituir os valores encontrados da inclinação e do ponto da tangente em sua equação:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(2,3) \end{array} \right\} \longrightarrow \ y -3= 4(x-2)$

A equação tangente é, portanto:

$\bm{y -3= 4(x-2)}$

Exercício 2

Calcule a equação da tangente à curva

$\displaystyle f(x)=-3x^2+2x$

na origem das coordenadas.

Veja a solução

A origem das coordenadas refere-se ao ponto

$(0,0).$

Devemos, portanto, calcular a tangente à função no ponto

$(0,0) .$

Primeiro, determinamos o valor da inclinação da tangente calculando a derivada na origem das coordenadas:

$f(x)=-3x^2+2x \ \longrightarrow \ f'(x)= -6x+2$

$f'(0)= -6\cdot 0+2=2$

$m=f'(0)=2$

Neste caso, já conhecemos um ponto por onde passa a tangente. Porque a afirmação nos diz que a reta deve ser tangente à curva na origem das coordenadas, ou seja, no ponto

$(0,0).$

Então o ponto que a curva e a tangente compartilham é o ponto

$(0,0).$

Por fim, basta substituir os valores encontrados para a inclinação e o ponto da tangente em sua equação:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=2 \qquad P(0,0) \end{array} \right\} \longrightarrow \ y -0= 2(x-0)$

Em conclusão, a equação tangente é:

$y -0= 2(x-0)$

$\bm{y = 2x}$

Exercício 3

Calcule a linha tangente à curva

$f(x)=x^2-2x-1$

que é paralelo à direita

$y-4x-6=0$

Veja a solução

Neste problema somos informados que a tangente deve ser paralela à reta

$y-4x-6=0 .$

E duas retas são paralelas se tiverem a mesma inclinação. A tangente deve, portanto, ter a mesma inclinação que a linha

$y-4x-6=0.$

Isso significa que precisamos encontrar a inclinação da reta

$y-4x-6=0 .$

Para fazer isso, limpamos a variável e:

$y-4x-6=0 \ \longrightarrow \ y =4x+6$

Então a inclinação da reta

$y=4x+5$

é 4, já que a inclinação de uma reta é o número que multiplica x quando y está claro.

Portanto, a inclinação da tangente também deve ser 4, pois para serem paralelas devem ter a mesma inclinação.

$m=4$

Neste caso não nos dizem o ponto de tangência entre a curva e a tangente. Mas sabemos que a derivada da curva no ponto de tangência é igual à inclinação da tangente, ou seja

$m=f'(x_0)$

. Bem, como podemos saber o valor de

$m$

, podemos encontrar x ₀ a partir da equação

$m=f'(x_0):$

Para fazer isso, primeiro calculamos a derivada de

$f(x):$

$f(x)= x^2-2x-1 \ \longrightarrow \ f'(x)=2x-2$

E agora resolvemos

$m=f'(x_0)$

sabendo que

$m = 4 :$

$m =f'(x_0)$

$4 =2(x_0)-2$

$4+2 =2x_0$

$6 =2x_0$

$\cfrac{6}{2} =x_0$

$3=x_0$

E uma vez que conhecemos a coordenada x do ponto, podemos encontrar a outra coordenada do ponto calculando

$f(3):$

$f(3)=3^2-2\cdot 3-1= 9-6-1=2$

Assim, o ponto pelo qual passam a curva e a tangente é o ponto

$(3,2).$

Resta substituir os valores encontrados da inclinação e do ponto da tangente em sua equação:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(3,2) \end{array} \right\} \longrightarrow \ y -2= 4(x-3)$

E a equação da tangente é:

$\bm{y -2=4(x-3)}$

Exercício 4

Calcule a linha tangente à curva

$f(x)=2x^2+5x+1$

que forma um ângulo de 45º com o eixo X.

Veja a solução

O enunciado do problema nos diz que a reta tangente deve formar um ângulo de 45º com o eixo X. Nestes casos, deve-se aplicar a seguinte fórmula para encontrar o valor da inclinação:

$m = \text{tg}\left(\alpha\right)$

$m = \text{tg}\left(45^{\text{o}}\right) = 1$

A instrução não especifica o ponto de tangência entre a curva e a linha tangente. Mas sabemos que a derivada da curva no ponto de tangência é equivalente à inclinação da tangente, ou seja

$m=f'(x_0)$

. Podemos, portanto, calcular x ₀ resolvendo a equação

$m=f'(x_0):$

Para fazer isso, primeiro calculamos a derivada de

$f(x):$

$f(x)=2x^2+5x+1\ \longrightarrow \ f'(x)=4x+5$