Ponto da equação – inclinação da reta

Nesta página você encontrará a fórmula da equação ponto-inclinação da reta e, também, as diferentes formas que existem para calculá-la. Além disso, você poderá ver diversos exemplos e praticar com exercícios resolvidos passo a passo.

Fórmula para a equação ponto-inclinação da reta

A equação ponto-inclinação de uma reta é uma forma de expressar matematicamente uma reta. Em particular, você só precisa da inclinação e das coordenadas de um ponto na reta para encontrar a equação ponto-inclinação de uma reta.

A fórmula para a equação ponto-inclinação da reta é a seguinte:

$y-y_0=m(x-x_0)$

Ouro

$m$

é a inclinação da linha e

$x_0, y_0$

são as coordenadas de um ponto na linha

$P(x_0,y_0).$

Vamos ver como a equação ponto-inclinação da reta é calculada usando um exemplo:

Escreva a equação ponto-inclinação da reta que passa pelo ponto
$P(2,-1)$

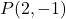
e inclinação m=3.

A fórmula para a equação ponto-inclinação da reta é a seguinte:

$y-y_0=m(x-x_0)$

Neste caso, a afirmação nos diz que a inclinação da reta é m=3, então a equação da reta será a seguinte:

$y-y_0=3(x-x_0)$

Além disso, sabemos também que a reta passa pelo ponto

$P(2,-1)$

, devemos, portanto, substituir as coordenadas deste ponto na equação:

$P(2,-1)$

$y-y_0=3(x-x_0) \ \xrightarrow{x_0=2 \ ; \ y_0=-1} \ y-(-1)=3(x-2)$

A equação ponto-inclinação da reta é, portanto:

$\bm{y+1=3(x-2)}$

Tenha em mente que além da equação ponto-inclinação, existem outras maneiras de expressar analiticamente uma reta: a equação vetorial, as equações paramétricas, a equação contínua, a equação implícita (ou geral) e a equação explícita de uma reta. Se você estiver mais interessado, pode conferir o que é cada um deles em nosso site.

O que significa a inclinação de uma linha?

Como vimos na definição da equação ponto-inclinação de uma reta, o parâmetro

$m$

é a inclinação da linha. Mas realmente… o que significa a inclinação de uma linha? Vamos ver isso a partir da representação gráfica de uma linha:

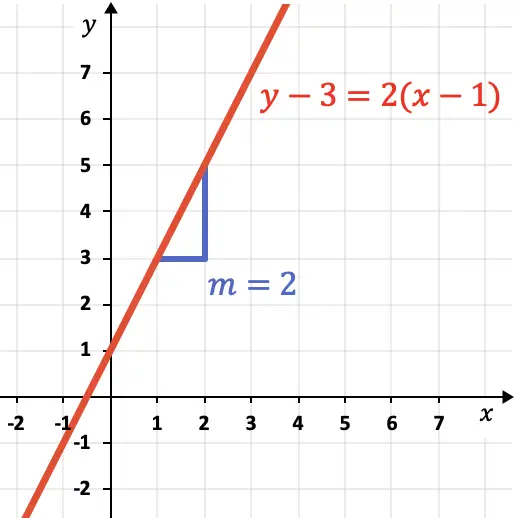
Qual é a equação ponto-inclinação de uma reta?

A inclinação da linha indica sua inclinação. Como você pode ver na linha do gráfico,

$m$

é igual a 2, pois a linha aumenta 2 unidades verticais para 1 unidade horizontal.

Obviamente, se a inclinação for positiva a função está aumentando (subindo), por outro lado se a inclinação for negativa a função está diminuindo (descendo).

Como calcular a inclinação de uma linha

Além disso, existem 3 maneiras diferentes de determinar numericamente a inclinação de uma linha:

Dados dois pontos diferentes na linha
$P_1(x_1,y_1)$

E

$P_2(x_2,y_2),$

A inclinação da linha é igual a:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Sim
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

é o vetor de direção da reta, sua inclinação é:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Sim
$\alpha$

é o ângulo formado pela reta com o eixo das abcissas (eixo X), a inclinação da reta é equivalente à tangente desse ângulo:

$m = \text{tg}(\alpha )$

fórmula para a equação explícita da reta

Posição relativa das linhas

Finalmente, a inclinação de uma linha também é usada para conhecer a relação entre várias linhas. Como duas retas paralelas têm a mesma inclinação e, por outro lado, se a inclinação de uma reta é o inverso negativo da inclinação de outra reta, isso significa que essas duas retas são perpendiculares .

Calcule a equação ponto-inclinação da reta que passa por dois pontos

Um problema muito comum é determinar a equação ponto-inclinação a partir de dois pontos pertencentes à reta. Vamos ver como isso é resolvido através de um exemplo:

Encontre a equação ponto-inclinação da reta que passa pelos dois pontos a seguir:

$P_1(5,2) \qquad P_2(3,6)$

Para determinar a equação ponto-inclinação da reta, precisamos determinar qual é o declive da reta. Portanto, calculamos a inclinação da reta usando a fórmula dos dois pontos:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{6-2}{3-5} = \cfrac{4}{-2}= -2$

Assim, a equação ponto-inclinação da reta será a seguinte:

$y-y_0=m(x-x_0)$

$y-y_0=-2(x-x_0)$

Portanto, precisamos apenas substituir as coordenadas cartesianas de um ponto da reta na equação:

$P_1(5,2)$

$y-y_0=-2(x-x_0) \ \xrightarrow{x_0=5 \ ; \ y_0=2} \ y-2=-2(x-5)$

$\bm{y-2=-2(x-5)}$

Também é bom colocarmos o outro ponto da afirmação na equação da reta:

$P_1(3,6)$

$y-6=-2(x-3)$

Encontre a equação ponto-inclinação de uma linha no gráfico

Como vimos nas seções acima, existem várias maneiras de determinar numericamente a equação ponto-inclinação de uma reta. No entanto, também pode ser encontrado graficamente. Vamos ver como isso é feito através de um exemplo:

Determine a equação ponto-inclinação da reta mostrada no gráfico a seguir:

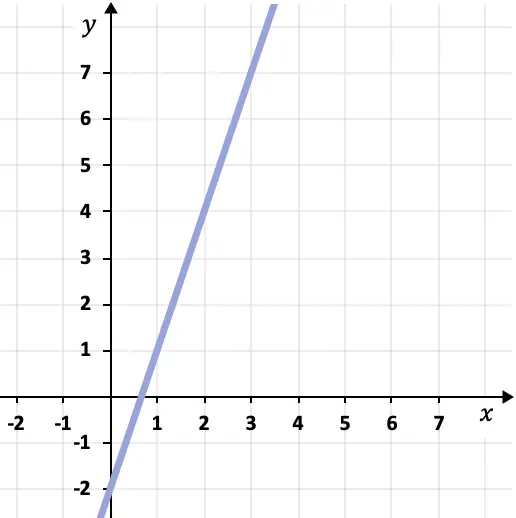
Para determinar a equação ponto-inclinação da reta desenhada, precisamos de determinar o seu declive e um ponto na reta.

Neste caso, a inclinação da reta é igual a 3, pois a reta sobe 3 unidades verticais para cada unidade horizontal.

$m = 3$

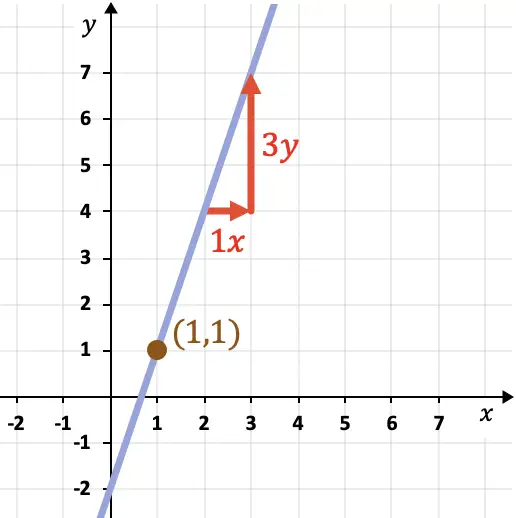
Em seguida, precisamos de um ponto na reta. Para fazer isso, podemos escolher qualquer ponto do gráfico por onde passa a reta, por exemplo o ponto (1,1).

$P(1,1)$

Portanto, podemos agora encontrar a equação ponto-inclinação da reta aplicando sua fórmula:

$y-y_0=m(x-x_0)$

$y-1=3(x-1)$

determinar graficamente a inclinação do ponto de equação de uma reta

Problemas resolvidos de equação ponto-inclinação

Exercício 1

Escreva a equação ponto-inclinação da reta que passa pelo ponto

$P(1,4)$

e sua inclinação é

$m=-2.$

veja solução

A fórmula para a equação ponto-inclinação da reta é:

$y-y_0=m(x-x_0)$

Neste caso, a afirmação nos diz que a inclinação da reta é m=-2, então a equação da reta será a seguinte:

$y-y_0=-2(x-x_0)$

Além disso, também sabemos pela afirmação que a reta passa pelo ponto

$P(1,4)$

, é portanto suficiente substituir as coordenadas do ponto na equação da reta:

$P(1,4)$

$\bm{y-4=-2(x-1)}$

Exercício 2

Qual é a equação ponto-inclinação da reta que passa pelos dois pontos a seguir?

$P_1(1,6) \qquad P_2(4,0)$

veja solução

Para determinar a equação ponto-inclinação da reta, precisamos determinar qual é o declive da reta. Portanto, calculamos a inclinação da reta com sua fórmula:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{0-6}{4-1} = \cfrac{-6}{3}= -2$

Assim, a equação ponto-inclinação da reta será a seguinte:

$y-y_0=m(x-x_0)$

$y-y_0=-2(x-x_0)$

Portanto, precisamos apenas substituir as coordenadas de um ponto da reta na equação:

$P_1(1,6)$

$\bm{y-6=-2(x-1)}$

Também teria sido correto colocar o outro ponto da afirmação na equação:

$y=-2(x-4)$

Exercício 3

Encontre a equação ponto-inclinação da reta que passa pelos dois pontos a seguir:

$P_1(1,-2) \qquad P_2(2,3)$

veja solução

Para encontrar a equação ponto-inclinação da reta, você deve primeiro calcular sua inclinação:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{3-(-2)}{2-1} = \cfrac{3+2}{1}=\cfrac{5}{1}= 5$

Assim, a equação ponto-inclinação da reta será a seguinte:

$y-y_0=m(x-x_0)$

$y-y_0=5(x-x_0)$

Portanto, precisamos apenas substituir as coordenadas de um ponto da reta na equação:

$P_1(1,-2)$

$y-(-2)=5(x-1)$

$\bm{y+2=5(x-1)}$

Também é correto colocar o outro ponto da afirmação na equação da reta:

$y-3=5(x-2)$

Exercício 4

Calcule a equação ponto-inclinação para a reta que forma um ângulo de 45º com o eixo X e passa pela origem das coordenadas.

veja solução

Se a linha fizer um ângulo de 45 graus com o eixo OX, sua inclinação será:

$m = \text{tg}(45º) = 1$

$y-y_0=1(x-x_0)$

$y-y_0=x-x_0$

E uma vez que conhecemos o declive da reta, podemos determinar a equação ponto-inclinação substituindo um ponto da reta na equação. Além disso, a afirmação nos diz que a reta passa pela origem das coordenadas, o que significa que ela passa pelo ponto (0,0). Ainda:

$P(0,0)$