Equação implícita, geral ou cartesiana do plano

Explicação de como a equação plana implícita (fórmula), também conhecida como equação geral ou cartesiana, é calculada. Além disso, você descobrirá como encontrar a equação do plano a partir de seu vetor normal. E ainda mais, você poderá ver exemplos e exercícios resolvidos passo a passo.

Qual é a equação implícita ou geral do plano?

Na geometria analítica, a equação implícita de um plano , também chamada de equação geral ou cartesiana do plano, é uma equação que permite expressar matematicamente qualquer plano. Para encontrar a equação implícita ou geral de um plano, precisamos de um ponto e de dois vetores linearmente independentes pertencentes a esse plano.

Fórmula da equação implícita ou geral do plano

Considere um ponto e dois vetores de direção de um plano:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

A equação implícita, geral ou cartesiana de um plano é obtida resolvendo o seguinte determinante e igualando o resultado a 0:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

Assim, a equação implícita ou geral do plano resultante será a seguinte:

$Ax+By+Cz+D=0$

É importante que os dois vetores da fórmula sejam linearmente independentes um do outro, ou seja, devem ter direções diferentes. E para que esta condição seja satisfeita basta que os dois vetores não sejam paralelos.

equação implícita ou geral ou cartesiana de pan xy em r3

Embora não seja necessário saber o motivo desta fórmula, você pode ver sua demonstração a seguir.

Partindo das equações paramétricas de um plano, passaremos para a equação implícita (ou geral) do plano:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Primeiro, passamos o termo independente de cada equação paramétrica para o outro lado da equação:

$\displaystyle \begin{cases}x-P_x= \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y-P_y = \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z-P_z = \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Ou equivalente:

$\displaystyle \begin{cases} \lambda \text{u}_x + \mu \text{v}_x =x-P_x\\[1.7ex] \lambda \text{u}_y + \mu \text{v}_y=y-P_y \\[1.7ex] \lambda\text{u}_z + \mu \text{v}_z =z-P_z\end{cases}$

Para que o sistema de equações acima tenha uma solução viável, a classificação da seguinte matriz deve ser igual a 2 (teorema de Rouche-Frobenius):

$\displaystyle\begin{pmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z\end{pmatrix}$

Portanto, se o contradomínio da matriz anterior deve ser dois, o determinante 3×3 deve necessariamente ser igual a zero:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

E resolvendo este determinante, obtemos a equação geral, implícita ou cartesiana de um plano:

$Ax+By+Cz+D=0$

Assim, acabamos de ver a equação implícita (ou geral) e as equações paramétricas do plano, porém, existem ainda mais maneiras de expressar um plano analiticamente, como a equação vetorial e a equação canônica. Você pode ver a fórmula e a explicação de todas as equações do plano neste link.

Exemplo de como encontrar a equação implícita ou geral do plano

Vejamos como determinar a equação implícita (ou geral ou cartesiana) de um plano através de um exemplo:

Encontre a equação implícita ou geral do plano que passa pelo ponto
$P(3,1,-1)$

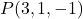
e contém os vetores

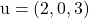
$\vv{\text{u}}=(2,0,3)$

E

$\vv{\text{v}}=(4,-1,2).$

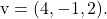
Para calcular a equação geral ou implícita do plano é necessário resolver o seguinte determinante formado pelos dois vetores, as variáveis e as coordenadas do ponto:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Então, substituímos os vetores e o ponto na fórmula:

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z-(-1) \end{vmatrix} =0$

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z+1 \end{vmatrix} =0$

E agora resolvemos o determinante de ordem 3, por exemplo com a regra de Sarrus ou por cofatores (ou deputados):

$-2(z+1)+12(y-1)+3(x-3)-4(y-1) = 0$

Agora operamos e agrupamos os termos:

$3(x-3)+8(y-1) -2(z+1) = 0$

$3x-9+8y-8 -2z-2 = 0$

$3x+8y-2z-19 = 0$

Portanto, a equação implícita ou geral do plano é:

$\bm{3x+8y-2z-19 = 0}$

Calcule a equação implícita ou geral de um plano a partir de seu vetor normal

Um problema muito típico nas equações de um plano é descobrir como é a equação de um determinado plano, dado um ponto e seu vetor normal (ou perpendicular). Então, vamos ver como funciona.

Mas primeiro você deve saber que as componentes X, Y, Z do vetor normal a um plano coincidem respectivamente com os coeficientes A, B, C da equação implícita (ou geral) desse plano.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Ouro

$\vv{n}$

é o vetor ortogonal ao plano

$\pi.$

Uma vez conhecida a relação anterior, vamos ver um exemplo de resolução deste tipo de problemas de equações planas:

Determine a equação implícita ou geral do plano que passa pelo ponto
$P(1,0,-2)$

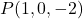
e um de seus vetores normais é

$\vv{n}=(3,-1,2) .$

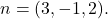
A fórmula para a equação implícita, geral ou cartesiana de um plano é:

$Ax+By+Cz+D=0$

Assim, a partir do vetor normal, podemos encontrar os coeficientes A, B e C porque são equivalentes às componentes do seu vetor normal:

$\vv{n}=(3,-1,2) \ \longrightarrow \ 3x-1y+2z+D=0$

Embora precisemos apenas encontrar o parâmetro D. Para isso, substituímos as coordenadas do ponto que pertence ao plano na equação:

$P(1,0,-2)$

$3\cdot 1-0+2\cdot (-2)+D=0$

$3-4+D=0$

$-1+D=0$

$D=1$

Portanto, a equação implícita ou geral do plano é:

$\bm{3x-y+2z+1 = 0}$

Problemas resolvidos da equação implícita ou geral do plano

Exercício 1

Encontre a equação implícita ou geral do plano que passa pelo ponto

$P(-2,1,3)$

e contém os vetores

$\vv{\text{u}}=(4,1,3)$

$\vv{\text{v}}=(5,3,-1).$

veja solução

Para calcular a equação geral ou implícita do plano é necessário resolver o seguinte determinante formado pelos dois vetores, pelas três variáveis e pelas coordenadas do ponto:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Então, substituímos os vetores e o ponto na fórmula:

$\displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0$

E agora resolvemos o determinante da matriz 3×3 com o método de sua escolha:

$12(z+1)+15(y-1)+1(x+2)-9(x+2)-4(y-1)-5(z+1) = 0$

Por fim, realizamos as operações e agrupamos termos semelhantes:

$-8(x+2)+11(y-1)+7(z+1) = 0$

$-8x-16+11y-11+7z+7=0$

$-8x+11y+7z-20= 0$

Portanto, a equação implícita ou geral do plano é:

$\bm{-8x+11y+7z-20 = 0}$

Exercício 2

Determine se o ponto

$P(-1,5,-3)$

pertence ao seguinte plano:

$\pi : \ 2x+y+6z-5=0$

veja solução

Para que o ponto esteja no plano, sua equação deve ser verificada. Portanto, precisamos substituir as coordenadas cartesianas do ponto na equação do plano e verificar se a equação é cumprida:

$2x+y+6z-5=0$

$P(-1,5,-3)$

$2\cdot (-1)+5+6\cdot (-3)-5=0$

$-2+5-18-5=0$

$-20\neq 0$

O ponto não respeita a equação do plano, portanto não faz parte deste plano.

Exercício 3

Encontre a equação implícita (ou geral) do plano que contém os três pontos a seguir:

$A(5,-1,-2) \qquad B(2,1,3) \qquad C(4,1,-2)$

veja solução

Para encontrar a equação implícita do plano, precisamos encontrar dois vetores linearmente independentes que se ligam no plano. E, para isso, podemos calcular dois vetores que são definidos pelos 3 pontos:

$\vv{AB} = B - A = (2,1,3) - (5,-1,-2) = (-3,2,5)$

$\vv{AC} = C - A = (4,1,-2) - (5,-1,-2) = (-1,2,0)$

As coordenadas dos dois vetores encontrados não são proporcionais, portanto são efetivamente linearmente independentes um do outro.

Agora já conhecemos dois vetores direções e um ponto do plano, então já podemos aplicar a fórmula da equação geral do plano:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Substituímos os vetores e um dos três pontos na fórmula:

$\displaystyle\begin{vmatrix}-3 & -1 & x-5 \\[1.1ex]2 & 2 & y+1 \\[1.1ex]5& 0 & z+2 \end{vmatrix} =0$