Equação explícita da reta

Nesta página você encontrará tudo sobre a equação explícita de uma reta: o que é, qual a sua fórmula, exemplos de cálculo, etc. Você também encontrará uma explicação detalhada do que significa inclinação e a interceptação da equação explícita. E, além disso, você verá diversos exemplos e poderá praticar com exercícios resolvidos passo a passo.

Qual é a equação explícita da reta?

Lembre-se de que a definição matemática de uma reta é um conjunto de pontos consecutivos representados na mesma direção, sem curvas ou ângulos.

Portanto, a equação explícita da reta é uma forma de expressar matematicamente qualquer reta. Para fazer isso, basta saber a inclinação da reta e o ponto onde ela cruza o eixo Y.

Fórmula para a equação explícita da reta

A fórmula para a equação explícita da reta é:

$y=mx+n$

Ouro

$m$

é a inclinação da linha e

$n$

sua interceptação em y, ou seja, a altura em que intercepta o eixo Y.

Vamos ver como a equação explícita da reta é calculada através de um exemplo:

Escreva a equação explícita da reta que passa pelo ponto
$P(3,1)$

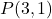
e inclinação m=2.

A fórmula para a equação explícita da reta é:

$y= mx+n$

Neste caso, a afirmação nos diz que a inclinação da reta é m=2, então a equação da reta será a seguinte:

$y= 2x+n$

É, portanto, suficiente calcular o coeficiente n. Para fazer isso, devemos substituir um ponto que pertence à reta em sua equação. E neste caso, a afirmação nos diz que a reta passa pelo ponto

$P(3,1),$

Ainda:

$P(3,1)$

$y= 2x+n \ \xrightarrow{x=3 \ ; \ y=1} \ 1=2\cdot 3 +n$

E resolvemos a equação resultante para encontrar o valor de n:

$1=2\cdot 3 +n$

$1=6 +n$

$1-6=n$

$-5 = n$

A equação explícita da reta é, portanto:

$\bm{y= 2x-5}$

Tenha em mente que além da equação explícita, existem outras maneiras de expressar analiticamente uma reta. Por exemplo, a equação vetorial , que é um tipo de equação de reta diferente de todas as outras porque o vetor de direção e um ponto da reta são expressos com suas próprias coordenadas. No link você confere o que é e porque é tão especial.

Significado dos parâmetros m e n

Como vimos na definição da equação explícita da reta, o parâmetro

$m$

é a inclinação da linha e

$n$

sua interceptação em y. Mas o que isso significa? Vamos ver isso a partir da representação gráfica de uma linha:

Qual é a equação explícita da reta y=mx+b

O termo independente

$\bm{n}$

é o ponto de intersecção da linha com o eixo do computador (eixo OY). No gráfico acima

$n$

é igual a 1 porque a linha cruza o eixo y em y=1.

Por outro lado, o termo

$\bm{m}$

indica a inclinação da linha , ou seja, sua inclinação. Como você pode ver no gráfico,

$m$

é igual a 2, pois a linha aumenta 2 unidades verticais para 1 unidade horizontal.

Obviamente, se a inclinação for positiva a função está aumentando (subindo), por outro lado se a inclinação for negativa a função está diminuindo (descendo).

Calcular a inclinação de uma linha

Além disso, existem 3 maneiras diferentes de determinar numericamente a inclinação de uma linha:

Dados dois pontos diferentes na linha
$P_1(x_1,y_1)$

E

$P_2(x_2,y_2),$

A inclinação da linha é igual a:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Sim
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

é o vetor de direção da reta, sua inclinação é:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Sim
$\alpha$

é o ângulo formado pela reta com o eixo das abcissas (eixo X), a inclinação da reta é equivalente à tangente desse ângulo:

$m = \text{tg}(\alpha )$

fórmula para a equação explícita da reta

Posição relativa das linhas

Finalmente, a inclinação de uma linha também é usada para conhecer a relação entre várias linhas. Como duas retas paralelas têm a mesma inclinação e, por outro lado, se a inclinação de uma reta é o inverso negativo da inclinação de outra reta, isso significa que essas duas retas são perpendiculares .

Calcule a equação explícita da reta que passa por dois pontos

Um problema muito típico é encontrar a equação explícita de uma reta dados dois pontos pelos quais ela passa. Vamos ver como isso é resolvido através de um exemplo:

Determine a equação explícita da reta que passa pelos dois pontos a seguir:

$P_1(4,-1) \qquad P_2(2,5)$

Para encontrar a equação explícita da reta, você precisa saber quanto valem os parâmetros m e n. Então, primeiro calculamos a inclinação da reta usando a fórmula dos dois pontos:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{5-(-1)}{2-4} = \cfrac{6}{-2}= -3$

$y=-3x+n$

E então podemos encontrar a interceptação y substituindo um ponto na reta na equação:

$P_1(4,-1)$

$y= -3x+n \ \xrightarrow{x=4 \ ; \ y=-1} \ -1=-3\cdot 4 +n$

$-1 =-12+ n$

$-1 +12= n$

$11= n$

Portanto, a equação explícita da reta é:

$\bm{y=-3x+11}$

Encontrando a equação explícita a partir da equação implícita

Finalmente, outro tipo de problema que frequentemente encontramos é encontrar a equação explícita da reta a partir de sua equação implícita (também chamada de equação geral ou cartesiana). Obviamente, para entender o método a seguir você precisa saber exatamente qual é a equação implícita e como ela é; mas se você não se lembra de nada, pode conferir no link.

Então, se você já domina a equação implícita (ou geral) de uma reta, vamos ver como funciona esse procedimento:

Encontre a equação explícita da seguinte reta:

$3x-2y+8 =0$

Tudo o que precisamos fazer para encontrar a equação explícita da reta é resolver a variável

$\bm{y}.$

Então passamos os termos sem

$y$

do outro lado da equação:

$-2y=-3x-8$

Agora limpamos a variável

$y:$

$\displaystyle y=\frac{-3x-8}{-2}$

E finalmente simplificamos:

$\displaystyle y=\frac{-3x}{-2} -\cfrac{8}{-2}$

$\displaystyle y=\frac{3x}{2} -(-4)$

$\displaystyle \bm{y=}\frac{\bm{3}}{\bm{2}}\bm{x +4}$

A inclinação desta reta é portanto

$\displaystyle \frac{3}{2}$

e sua interceptação em y é 4.

Problemas de equações explícitas resolvidos

Exercício 1

Dê a inclinação e a interceptação em y das seguintes retas:

$\begin{array}{lll} A) \ y= 3x-1 & \qquad & B) \ y=5x+2 \\[2ex] C) \ y=-x+3 & \qquad & D) \ 4x+2y-6=0 \end{array}$

veja solução

A equação explícita de uma reta segue a seguinte fórmula:

$y=mx+n$

Ouro

$m$

é a inclinação e

$n$

o computador na origem. Ainda:

$\bm{A)} \ y= 3x-1 \ \begin{cases} m = 3 \\[2ex] n=-1\end{cases}$

$\bm{B)} \ y= 5x+2 \ \begin{cases} m = 5 \\[2ex] n=2 \end{cases}$

$\bm{C)} \ y= -x+3 \ \begin{cases} m = -1 \\[2ex] n=3\end{cases}$

A última reta é expressa por sua equação implícita, então primeiro precisamos passá-la para uma equação explícita (resolver para

$y$

) então podemos identificar os parâmetros:

$\bm{D)} \ 4x+2y-6=0$

$2y =-4x+6$

$y =\cfrac{-4x+6}{2}$

$y =-2x+3$

$\begin{cases} m = -2 \\[2ex] n=3 \end{cases}$

Exercício 2

Encontre a equação explícita da reta que passa pelo ponto

$P(2,-3)$

e tem a inclinação

$m=-2.$

veja solução

A fórmula para a equação explícita da reta é:

$y= mx+n$

Neste caso, a inclinação da reta deve ser -2, então a equação da reta terá a seguinte forma:

$y= -2x+n$

É, portanto, suficiente calcular o coeficiente n. Para fazer isso, você deve substituir um ponto pertencente à reta em sua equação e resolver a equação resultante:

$P(2,-3)$

$y= -2x+n \ \xrightarrow{x=2 \ ; \ y=-3} \ -3=-2\cdot 2 +n$

$-3=-4 +n$

$-3+4= n$

$1= n$

Resumindo, a equação explícita da reta é:

$\bm{y= -2x+1}$

Exercício 3

Encontre a equação explícita da reta que passa pelos dois pontos a seguir:

$P_1(6,-1) \qquad P_2(3,2)$

veja solução

Para encontrar a equação explícita da reta, você precisa saber quanto valem os parâmetros m e n. Portanto, primeiro calculamos a inclinação da reta a partir das coordenadas dos dois pontos:

$m = \cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{2-(-1)}{3-6} = \cfrac{3}{-3}= -1$

$y=-x+n$

E então determinamos a interceptação substituindo um ponto da reta na equação:

$P_1(6,-1)$

$y= -x+n \ \xrightarrow{x=6 \ ; \ y=-1} \ -1=-6 +n$

$-1 +6= n$

$5= n$

Portanto, a equação explícita da reta é:

$\bm{y=-x+5}$

Exercício 4

Calcule a equação explícita da reta que forma um ângulo de 45º com o eixo X e passa pela origem das coordenadas.

veja solução

Se a linha fizer um ângulo de 45 graus com o eixo OX, sua inclinação será:

$m = \text{tg}(45º) = 1$

$y=x+n$

E uma vez que conhecemos o declive da reta, podemos calcular a interseção y substituindo um ponto da reta na equação. Além disso, a afirmação nos diz que a reta passa pela origem das coordenadas, o que significa que ela passa pelo ponto (0,0). Ainda:

$P(0,0)$

$y= x+n \ \xrightarrow{x=0 \ ; \ y=0} \ 0=0 +n$

$0= n$

Portanto, a equação explícita da reta é:

$\bm{y=x}$

Exercício 5

Encontre a equação explícita da reta paralela à reta

$r$

e o que acontece além do ponto

$P(-2,4).$

ser direto

$r:$

$r: \; y=3x+4$

veja solução

Para que a linha seja paralela à linha

$r,$

ambos devem ter a mesma inclinação, portanto:

$m = 3$

$y=3x+n$

E uma vez que conhecemos a inclinação da reta, podemos calcular a interceptação y substituindo o ponto que pertence à reta na equação:

$P(-2,4)$

$y= 3x+n \ \xrightarrow{x=-2 \ ; \ y=4} \ 4=3\cdot (-2) +n$

$4=-6+ n$

$4+6= n$

$10= n$

Portanto, a equação explícita da reta é:

$\bm{y=3x+10}$

Exercício 6

Qual é a equação explícita de cada linha representada graficamente?

equação explícita da linha exercício resolvido passo a passo

veja solução

azul à direita

A linha azul aumenta um Y para cada

$y =x+2$

verde direito

A linha verde aumenta em 3 Ys para cada X, então sua inclinação é 3. Além disso, a linha cruza o eixo Y em -4, então sua interceptação em y é -4.

$y =3x-4$

Linha Vermelha

A linha vermelha diminui em dois Y para cada X, então sua inclinação é -2. E a reta intercepta o eixo y em y=-2, então sua interceptação em y também é -2.

$y =-2x-2$

Qual é a equação explícita da reta?

Fórmula para a equação explícita da reta

Significado dos parâmetros m e n

Calcular a inclinação de uma linha

Posição relativa das linhas

Calcule a equação explícita da reta que passa por dois pontos

Encontrando a equação explícita a partir da equação implícita

Problemas de equações explícitas resolvidos

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Exercício 6

Deixe um comentário Cancelar resposta