Equação de circunferência -

Nesta página você encontrará tudo sobre a equação da circunferência: equação ordinária, equação geral, outros tipos de equações da circunferência, quando a equação de uma circunferência está correta,… Além disso, você verá exemplos de como encontrar o equação de uma circunferência e você pode praticar com exercícios resolvidos.

Equação ordinária do círculo

Antes de ver o que é a equação da circunferência, vamos relembrar a noção de circunferência:

A circunferência é o lugar geométrico dos pontos do plano equidistantes de um ponto fixo denominado centro.

Portanto, todos os pontos de um círculo estão à mesma distância do seu centro.

Além disso, o círculo é uma das quatro seções cônicas junto com a elipse, a parábola e a hipérbole. Ou seja, um círculo pode ser obtido cortando-se um cone com um plano paralelo à sua base.

A maneira mais simples de descrever um círculo no plano cartesiano é a partir de sua equação ordinária. Portanto, a fórmula para a equação ordinária da circunferência é a seguinte:

A equação ordinária do círculo é:

$(x-a)^2+(y-b)^2=r^2$

Ouro:

$r$

é o raio do círculo.
$a$

E

$b$

são as coordenadas do centro do círculo:

$C(a,b)$

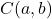
Embora não a demonstremos por ser um pouco tedioso, esta equação pode ser obtida a partir do teorema de Pitágoras.

Vamos ver como a equação ordinária de um círculo é calculada com um exemplo:

Determine a equação ordinária do círculo de raio 5 cujo centro é o ponto
$C(3,-1).$

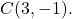
A fórmula para a equação ordinária de um círculo é:

$(x-a)^2+(y-b)^2=r^2$

Portanto, só temos que substituir a incógnita

$r$

pelo valor do raio, e as incógnitas

$a$

$b$

pelas coordenadas X e Y respectivamente do centro do círculo:

$(x-3)^2+(y-(-1))^2=5^2$

Portanto, a equação ordinária da circunferência é:

$\bm{(x-3)^2+(y+1)^2=25}$

Equação geral do círculo

Outro tipo de equação de circunferência é a equação geral, aliás é a mais utilizada. Veremos então como obter a equação geral de qualquer circunferência a partir da sua equação ordinária.

Considere a equação ordinária de um círculo:

$(x-a)^2+(y-b)^2=r^2$

Se desenvolvermos as igualdades notáveis (ou produtos notáveis):

$x^2+a^2-2ax+y^2+b^2-2by=r^2$

$x^2-2ax+y^2-2by+a^2+b^2-r^2=0$

Agora fazemos 3 alterações de variáveis:

$A=-2a \qquad B=-2b \qquad C=a^2+b^2-r^2$

E finalmente obtemos a equação geral da circunferência:

$x^2+y^2+Ax+By+C=0$

A fórmula para a equação geral da circunferência é, portanto:

$x^2+y^2+Ax+By+C=0$

onde o centro do círculo é:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

E o raio do círculo é:

$\displaystyle r=\sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C}$

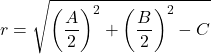
Portanto, esta equação da circunferência é sempre obtida pela equação ordinária. Aqui está um exemplo para ver como isso é feito:

Determine a equação geral do círculo de raio 6 cujo centro é o ponto
$C(2,4).$

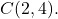
Primeiro precisamos encontrar a equação ordinária da circunferência. Para fazer isso, usamos sua fórmula:

$(x-a)^2+(y-b)^2=r^2$

$(x-2)^2+(y-4)^2=6^2$

E agora operamos até encontrarmos a equação geral da circunferência, ou seja, até não podermos mais simplificar:

$x^2+2^2-2\cdot x \cdot 2+y^2+4^2-2\cdot y \cdot 4=36$

$x^2+4-4x+y^2+16-8y=36$

$x^2-4x+y^2-8y+4+16-36=0$

$x^2-4x+y^2-8y-16=0$

Portanto a equação geral da circunferência é:

$\bm{x^2+y^2-4x-8y-16=0}$

Embora o problema não exigisse isso, podemos agora calcular o centro e o raio da equação encontrada para verificar se está correta.

Para determinar o centro do círculo, usamos sua fórmula:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

$\displaystyle C\left(-\frac{-4}{2}, -\frac{-8}{2}\right)$

$\displaystyle C\bigl(-(-2), -(-4)\bigr)$

$\displaystyle C\left(2,4\right)$

Na verdade, o centro do círculo coincide com o da afirmação.

Também verificamos o raio da circunferência com sua fórmula:

$\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{-4}{2}\right)^2 +\left(\frac{-8}{2}\right)^2-(-16)} \\[2ex] & =\sqrt{\left(-2\right)^2 +\left(-4\right)^2+16} \\[2ex] &= \sqrt{4+16+16} \\[2ex] &= \sqrt{36} \\[2ex] & = 6 \end{aligned}$

E o raio também é igual ao da afirmação. Portanto, a equação da circunferência calculada está correta.

Existência de uma circunferência

Todas as equações na forma de

$x^2+y^2+Ax+By+C=0$

correspondem a um círculo. Assim, para que este tipo de expressão seja verdadeiramente a equação de um círculo, as 3 condições a seguir devem ser atendidas:

Os coeficientes de
$x^2$

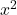
e de

$y^2$

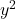
eles devem ser iguais a 1. Lembre-se de que se ambas as variáveis fossem precedidas por um número diferente de um, mas ambas tivessem o mesmo número, toda a equação poderia ser dividida por esse número para que seus coeficientes fossem 1.
A equação não pode ter um termo
$xy.$
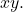
A seguinte expressão deve ser positiva:

As duas equações circulares que vimos, a equação ordinária e a equação geral, são as mais utilizadas para expressar matematicamente uma circunferência no plano (em R2). Porém, existem vários tipos de equações para descrever este objeto geométrico, abaixo está a explicação de cada uma delas.

Equação canônica do círculo

A equação canônica, ou equação reduzida, de um círculo é usada para descrever qualquer círculo cujo centro está na origem das coordenadas , ou seja, no ponto (0,0). A referida equação é a seguinte:

$x^2+y^2=r^2$

Se, além disso, o raio fosse equivalente à unidade (1), a equação da circunferência seria:

$x^2+y^2=1$

Esta última equação corresponde à circunferência goniométrica, também chamada de circunferência unitária ou círculo unitário. É o círculo de raio 1 centrado na origem das coordenadas.

Equações de dois círculos concêntricos

Duas equações concêntricas são aquelas que têm o centro no mesmo ponto. E a única coisa diferente que dois círculos concêntricos têm é o raio.

Portanto, para que esta condição seja satisfeita, as equações de dois círculos concêntricos são exatamente iguais, exceto pelos seus termos independentes, que devem ser diferentes.

$x^2+y^2+Ax+By+C=0$

$x^2+y^2+Ax+By+C'=0$

Por exemplo, os dois círculos seguintes são concêntricos, uma vez que todos os seus coeficientes são idênticos, exceto os termos independentes:

$x^2+y^2+3x-4y+1=0$

$x^2+y^2+3x-4y+5=0$

Equação paramétrica do círculo

Assim como a reta, a equação de um círculo também pode ser parametrizada com as funções trigonométricas de seno e cosseno. Assim, as equações paramétricas do círculo são:

$\diplaystyle \begin{cases}x= a + r \cdot \text{cos}(t) \\[2ex] y= b + r\cdot \text{sen}(t)\end{cases} \qquad t\in[0,2\pi)$

onde o ponto

$(a,b)$

é o centro do círculo e

$r$

Este é o seu departamento.

Problemas resolvidos da equação de um círculo

Exercício 1

Calcule a equação geral do círculo de raio 5 cujo centro está no ponto

$C(-1,2).$

veja solução

Para determinar a equação geral da circunferência, devemos primeiro determinar a sua equação ordinária. Para fazer isso, usamos a fórmula da equação ordinária de um círculo:

$(x-a)^2+(y-b)^2=r^2$

$(x-(-1))^2+(y-2)^2=5^2$

$(x+1)^2+(y-2)^2=25$

Uma vez conhecida a equação ordinária, trabalhamos até encontrar a equação geral da circunferência:

$x^2+1^2+2\cdot x \cdot 1+y^2+2^2-2\cdot y \cdot 2=25$

$x^2+1+2x+y^2+4-4y=25$

$x^2+2x+y^2-4y+1+4-25=0$

$x^2+2x+y^2-4y-20=0$

Portanto a equação geral da circunferência é:

$\bm{x^2+y^2+2x-4y-20=0}$

Exercício 2

Para cada um dos círculos a seguir, encontre as coordenadas do seu centro e o comprimento do seu raio.

$\text{A)}\ (x-2)^2+(y+5)^2=36$

$\text{B)}\ x^2+y^2+8x-10y+1 = 0$

$\text{C)}\ x^2+y^2=4$

veja solução

circunferência A)

$(x-2)^2+(y+5)^2=36$

A circunferência é expressa na forma de uma equação ordinária, cuja fórmula é:

$(x-a)^2+(y-b)^2=r^2$

Portanto, as coordenadas do centro do círculo são:

$C(a,b)$

$\bm{C(2,-5)}$

E seu raio é:

$r^2=36$

$\bm{r=6}$

circunferência B)

$x^2+y^2+8x-10y+1 = 0$

Esta circunferência é expressa na forma de uma equação geral, portanto para calcular as coordenadas do seu centro deve-se utilizar a seguinte fórmula:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

$\displaystyle C\left(-\frac{8}{2}, -\frac{-10}{2}\right)$

$\displaystyle C\bigl(-4, -(-5)\bigr)$

$\displaystyle \bm{C(-4, 5)}$

Por outro lado, a fórmula para encontrar o raio do círculo é:

$\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{8}{2}\right)^2 +\left(\frac{-10}{2}\right)^2-1} \\[2ex] & =\sqrt{\left(4\right)^2 +\left(-5\right)^2-1} \\[2ex] &= \sqrt{16+25-1} \\[2ex] &= \bm{\sqrt{40}} \end{aligned}$

circunferência C)

$x^2+y^2=4$

A circunferência é expressa na forma de uma equação ordinária, cuja fórmula é:

$(x-a)^2+(y-b)^2=r^2$

Portanto, as coordenadas do centro do círculo são:

$C(a,b)$

Neste caso, a equação não tem termo.

$a$

nenhum

$b,$

está, portanto, centrado na origem das coordenadas:

$\bm{C(0,0)}$

E seu raio é:

$r^2=4$

$\bm{r=2}$

Exercício 3

Qual das seguintes equações é a equação de um círculo?

$\text{A)}\ x^2+y^2+4x-6y-1=0$

$\text{B)}\ x^2+y^2+5x+5y+2xy-4 = 0$

$\text{C)}\ 2x^2+2y^2-8x+4y+2=0$

$\text{D)}\ x^2+y^2+x+2y+6=0$

veja solução

Para que uma expressão seja a equação de um círculo, as seguintes condições devem ser verdadeiras:

1. Os coeficientes de

$x^2$

e de

$y^2$

Eles devem ser iguais a 1.
2. A equação não pode ter termo

$xy.$

Equação A)

$x^2+y^2+4x-6y-1=0$

Os coeficientes de

$x^2$

$y^2$

são 1 e a equação não tem termo

$xy.$

Basta, portanto, verificar a terceira condição:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”190″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”216″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”22″ width=”146″ style=”vertical-align: -5px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”103″ style=”vertical-align: -2px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”49″ style=”vertical-align: -2px;”> <p class=$ 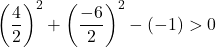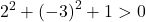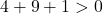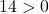A equação satisfaz as 3 condições, portanto é a equação de um círculo.

Equação B)

$x^2+y^2+5x+5y+2xy-4 = 0$

A equação tem um termo com

$xy,$

com o qual a equação não corresponde a um círculo.

Equação C)

$2x^2+2y^2-8x+4y+2=0$

Os coeficientes de

$x^2$

$y^2$

não são 1, mas podemos transformar a equação dividindo todos os termos:

$x^2+y^2-4x+2y+1=0$

Desta forma agora os coeficientes de

$x^2$

$y^2$

sim, eles são 1 e, além disso, a equação não tem termo

$xy.$

Portanto, só temos que corroborar a terceira condição:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”190″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”189″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”22″ width=”158″ style=”vertical-align: -5px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”103″ style=”vertical-align: -2px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”42″ style=”vertical-align: -2px;”> <p class=$ 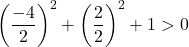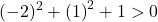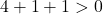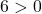A equação satisfaz as 3 condições, portanto é a equação de um círculo.

Equação D)

$x^2+y^2+x+2y+6=0$

Os coeficientes de

$x^2$

$y^2$

são 1 e a equação não tem termo

$xy.$

Basta, portanto, verificar a terceira condição:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”190″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”175″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”128″ style=”vertical-align: -4px;”> } \ 0″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”82″ style=”vertical-align: -4px;”> <p class=$ 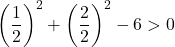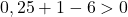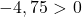A equação não satisfaz a última condição, portanto não é a equação de um círculo .

Exercício 4

Determine a equação da circunferência que passa pelos três pontos a seguir:

$A(0,0) \quad B(3,0) \quad C(2,-2)$

veja solução

A equação geral de qualquer círculo é:

$x^2+y^2+Ax+By+C=0$

Portanto, precisamos substituir as coordenadas dos pontos na equação do círculo para encontrar os parâmetros

$A,$

$B$

$C.$

Com o primeiro ponto de encontramos o coeficiente

$C:$

$A(0,0) \ \longrightarrow \ 0^2+0^2+A\cdot 0 +B\cdot 0+C=0 \ \longrightarrow \ \bm{C = 0}$

Com o segundo ponto encontramos o coeficiente

$A:$

$\begin{aligned}A(3,0) \ \longrightarrow \ & 3^2+0^2+A\cdot 3 +B\cdot 0+C=0 \\[2ex] & 9+A\cdot 3 =0\\[2ex]& \bm{A=-3} & \end{aligned}$

E a partir do terceiro ponto encontramos o coeficiente

$B:$

$\begin{aligned} A(2,-2) \ \longrightarrow \ & 2^2+(-2)^2+A\cdot 2 +B\cdot (-2)+C=0 \\[2ex] & 4+4+(-3)\cdot 2+ B\cdot (-2)+0=0 \\[2ex] & 8-6-2B=0 \\[2ex] & \bm{B=1} \end{aligned}$

Em conclusão, a equação geral para circunferência é:

$\bm{x^2+y^2-3x+y=0}$

Exercício 5

Se as extremidades opostas de um círculo são os dois pontos a seguir:

$A(2,3) \qquad B(6,-1)$

Qual é a equação ordinária do círculo?

veja solução

Se os dois pontos forem extremos do círculo, seu centro será o ponto médio entre esses dois pontos:

$\displaystyle C\left(\frac{2+6}{2} , \frac{3+(-1)}{2} \right)$

$\displaystyle C\left(\frac{8}{2} , \frac{2}{2} \right)$

$\displaystyle C\left(4,1 \right)$

Por outro lado, o diâmetro do círculo será a distância entre os dois pontos, que pode ser calculada utilizando a magnitude do vetor que os dois pontos formam:

$\vv{AB} = B-A=(6,-1) - (2,3) = (4,-4)$

$d = \lvert \vv{AB} \rvert =\sqrt{4^2+(-4)^2} = \sqrt{16+16} = \sqrt{32}$

E o raio do círculo é metade do diâmetro:

$r = \cfrac{\sqrt{32}}{2}$

A equação ordinária do círculo é, portanto:

$(x-a)^2+(y-b)^2=r^2$

$\displaystyle (x-4)^2+(y-1)^2=\left(\frac{\sqrt{32}}{2}\right)^2$

$\displaystyle \bm{(x-4)^2+(y-1)^2=}\frac{\bm{32}}{\bm{4}}$

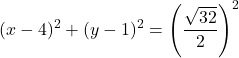
Por fim, se este artigo foi útil para você, certamente também se interessará por nossas páginas de hipérbole (matemática) e parábola (matemática) . Você encontrará uma explicação detalhada do que são a hipérbole e a parábola, suas equações, suas características, exemplos, exercícios resolvidos…

Equação ordinária do círculo

Equação geral do círculo

Existência de uma circunferência

Equação canônica do círculo

Equações de dois círculos concêntricos

Equação paramétrica do círculo

Problemas resolvidos da equação de um círculo

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Deixe um comentário Cancelar resposta