Nesta página você descobrirá como dividir polinômios, tanto a divisão de um polinômio por um monômio quanto a divisão de um polinômio por outro polinômio. Você também poderá ver exemplos de divisão de polinômios e praticar exercícios resolvidos passo a passo. Além disso, você encontrará as propriedades desta operação polinomial.
Divisão polinomial (ou polinomial)
Antes de vermos exatamente como dois polinômios são divididos, revisaremos brevemente os conceitos de divisão polinomial, para que então seja mais fácil entender o método que vamos utilizar.
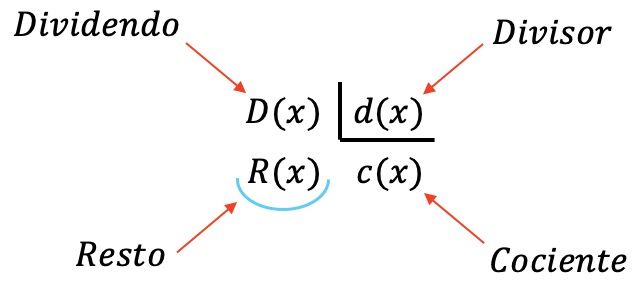
Quatro polinômios estão envolvidos em uma divisão polinomial:
- Dividendo : o polinômio dividido.
- Divisor : o polinômio que divide o dividendo.
- Quociente : resultado da divisão do dividendo pelo divisor.
- Resto (ou resíduo): o polinômio restante na divisão entre os dois polinômios.
Por outro lado, você também deve saber que existem dois tipos de divisão entre polinômios:
- Divisão exata de polinômios : uma divisão entre polinômios é exata quando o resto é zero. Neste caso, o dividendo polinomial é igual ao divisor multiplicado pelo quociente.
Além disso, neste caso, o dividendo
é um múltiplo do divisor
e o quociente
Da mesma forma, o divisor polinomial e o quociente polinomial são ambos divisores do dividendo.
- Divisão inteira de polinômios : em uma divisão inteira (ou inexata) de polinômios o resto é diferente de zero (0). Então, a propriedade fundamental da divisão polinomial é satisfeita:
Agora que vimos o que é dividir polinômios, vamos ver como dividir polinômios entre si. Mais precisamente, explicaremos primeiro a divisão entre um polinômio e um monômio e depois a divisão entre 2 polinômios.
Divisão de um polinômio por um monômio
Antes de ver como dividir um polinômio por um monômio, vamos primeiro lembrar como os monômios são divididos entre eles, pois é necessário conhecê-lo para poder fazer este tipo de operação polinomial.
A divisão de dois monômios envolve dividir seus coeficientes entre si e suas partes literais entre si, ou seja, dividem-se os coeficientes dos monômios e subtraem-se os expoentes das variáveis que possuem a mesma base. Veja o exemplo a seguir:
Agora vamos ver o que envolve a divisão de um polinômio por um monômio:
Em matemática, para resolver a divisão de um polinômio por um monômio, cada termo do polinômio é dividido pelo monômio.
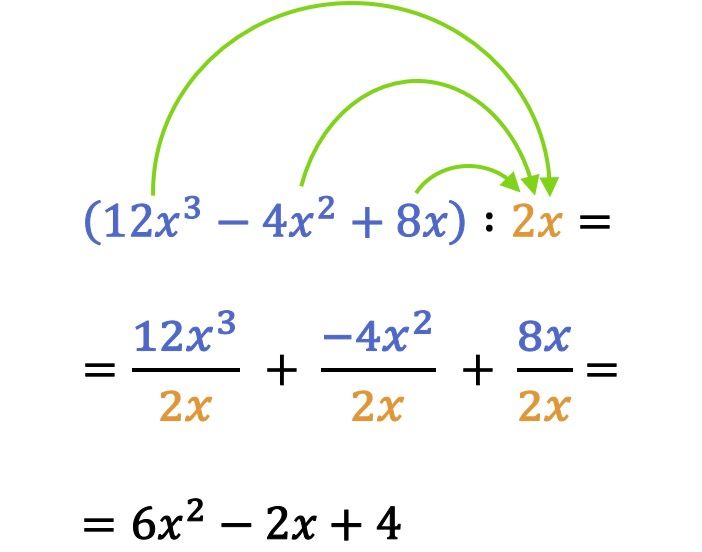
Observe no exemplo de divisão anterior que ao dividir monômios ou polinômios você também deve levar em consideração a regra dos sinais. Na verdade, um erro muito comum nas divisões entre polinômios e monômios é errar o sinal de um termo.
Divisão de um polinômio por outro polinômio
Para dividir dois polinômios, é necessário seguir um procedimento, então vamos ver como fica o método de divisão de polinômios, também chamado de divisão longa de polinômios, resolvendo um exemplo passo a passo:
- Calcule o resultado da divisão do polinômio
entre o polinômio
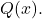
Sendo os dois polinômios:
A primeira coisa a fazer é colocar os polinômios na forma de divisão. À esquerda escrevemos o numerador da fração (polinômio dividendo) e à direita colocamos o denominador da fração (polinômio divisor):
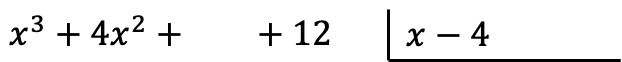
Atenção: Se um polinômio não possui um monômio de certo grau, devemos deixar um espaço em seu lugar. Por exemplo, o polinômio
Não há período de primeiro ano, portanto há um espaço em branco.
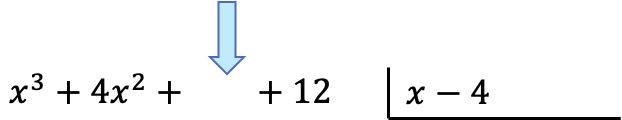
Assim que tivermos os polinômios no lugar, vamos encontrar o quociente. E para encontrar o primeiro termo do quociente devemos dividir o primeiro termo do dividendo pelo primeiro termo do divisor:
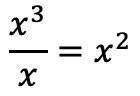
E colocamos o resultado da divisão no lugar do quociente:
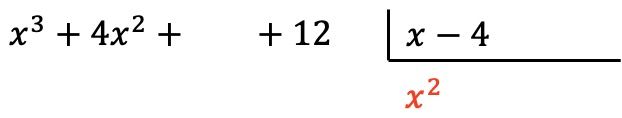
Agora multiplicamos o termo encontrado por cada elemento do divisor, e colocamos cada resultado abaixo do dividendo em sua coluna correspondente , mudando seu sinal :
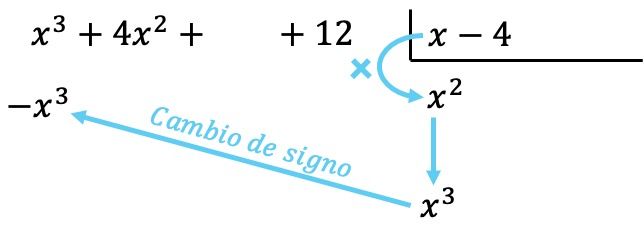
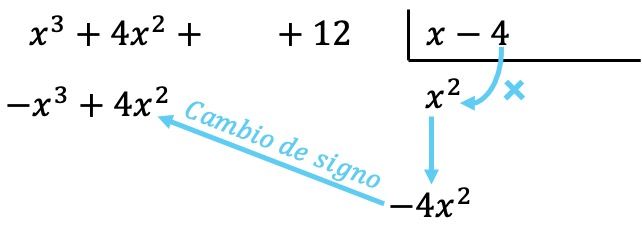
Como em todas as operações com polinômios, é importante ordenar os polinômios do grau mais alto para o grau mais baixo, de modo que todos os termos do mesmo grau estejam na mesma coluna.
Depois de colocarmos os resultados da multiplicação com o sinal oposto, precisamos adicionar os termos alinhados verticalmente:
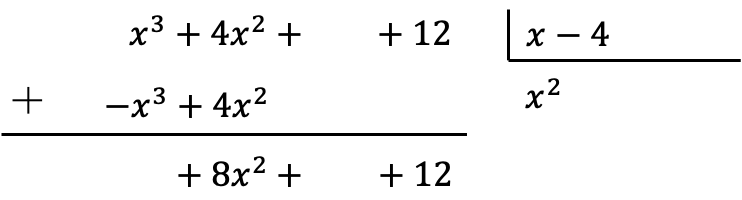
Observe que ao fazer essa soma, o coeficiente de maior grau se anula e, portanto, temos um termo a menos no dividendo.
Agora precisamos repetir o mesmo procedimento até que o dividendo polinomial seja um grau menor que o divisor polinomial.
Portanto, dividimos o primeiro termo do dividendo pelo primeiro termo do divisor:
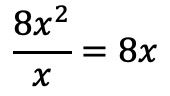
Colocamos o resultado no quociente:
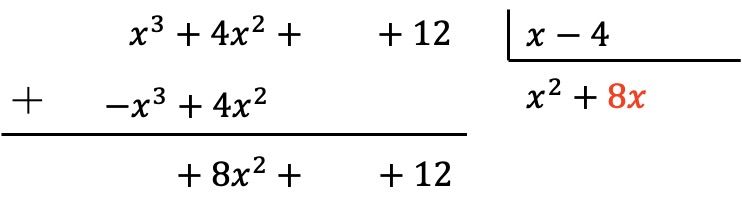
Como antes, multiplicamos o novo termo do quociente por cada elemento do divisor e colocamos os resultados de sinal oposto nas colunas correspondentes do dividendo:
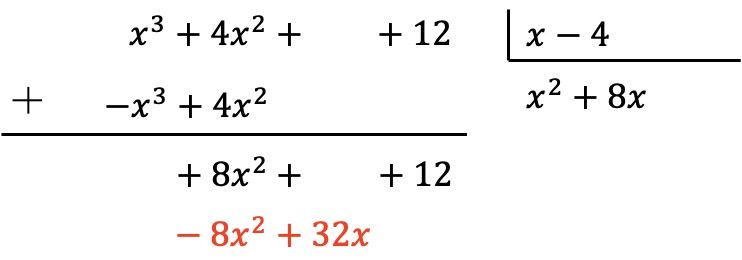
E adicionamos verticalmente:
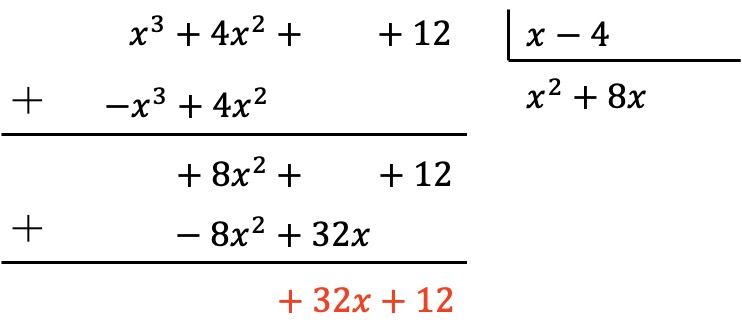
O polinômio do dividendo ainda não é um grau menor que o polinômio divisor, então precisamos continuar fazendo o mesmo processo.
Então primeiro dividimos o primeiro termo do dividendo pelo primeiro termo do divisor, depois multiplicamos o resultado por cada termo do divisor, depois colocamos os resultados modificados em sinal no dividendo e, por fim, somamos verticalmente:
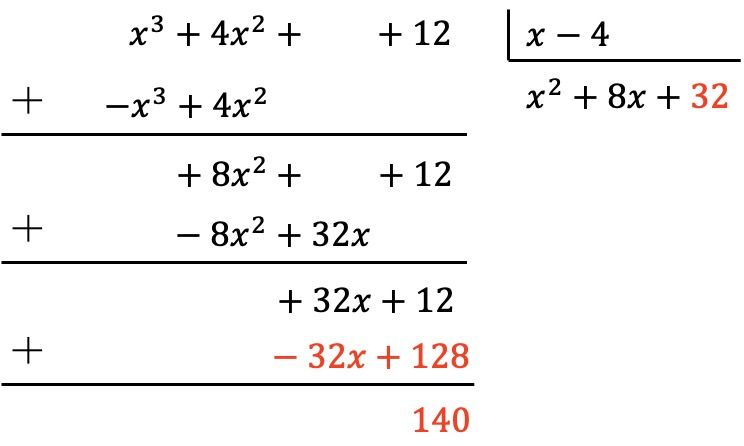
Então já obtivemos que o polinômio do dividendo é de grau menor que o grau do divisor, pois o dividendo é de grau 0 e o divisor é de grau 1. Portanto, a divisão está completa.
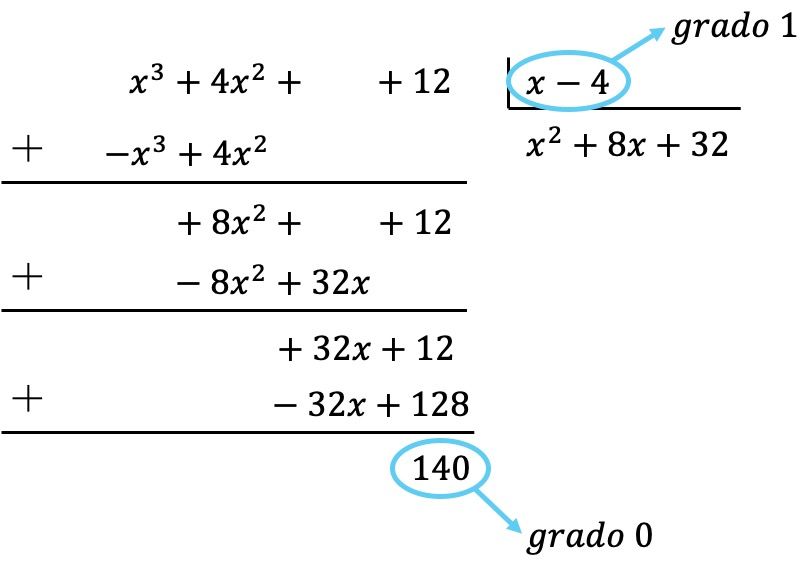
O resultado da divisão é portanto:
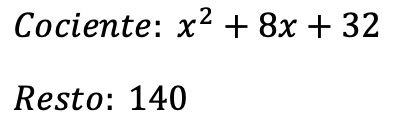
Por outro lado, podemos verificar que realizamos corretamente a divisão polinomial com base na condição fundamental para a divisão de polinômios:
✅
A equação está satisfeita, então a divisão polinomial foi realizada corretamente.
Para terminarmos a divisão de polinômios, esperamos ter ajudado você com esta explicação. O que você achou do método de divisão de polinômios? Você tem alguma dúvida? Você gosta disso? Ou você preferiria que não existissem divisões polinomiais? 😂 Lemos você nos comentários! 👇👇👇
Propriedades da divisão de polinômios
Qualquer divisão de polinômios atende às seguintes características:
✓ O grau do dividendo polinomial deve ser sempre maior que o grau do divisor polinomial.
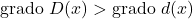✓ O grau do dividendo polinomial equivale à soma dos graus do divisor e do quociente.
✓ O grau do resto é sempre menor que o grau do divisor (e portanto também do dividendo).
✓ O dividendo é igual ao produto do divisor vezes o quociente mais o resto. Esta condição também é colocada na divisão de números.
Exercícios resolvidos sobre divisão de polinômios
Exercício 1
Determine o resultado da seguinte divisão de um polinômio por um monômio:
Para dividir um polinômio por um monômio você deve resolver a divisão de cada termo do polinômio pelo referido monômio:
![\begin{aligned} \left(15x^5+9x^3 \right) : \left(3x^2\right) & = \cfrac{15x^{5}}{3x^2}+ \cfrac{9x^3}{3x^2} \\[2ex] & = \bm{5x^3+3x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ffa558b26adc36e2ac45a842a6cf33df_l3.png "Rendered by QuickLaTeX.com")
Lembre-se que na divisão entre monômios, os coeficientes são divididos entre si e os expoentes das potências cuja base é a mesma são subtraídos.
Exercício 2
Calcule a seguinte divisão de um polinômio por um monômio:
Para dividir um polinômio por um monômio você deve dividir cada termo do polinômio pelo referido monômio:
![\begin{aligned} \left( 16x^5-4x^3-20x^2 \right) : \left(4x^2\right) & = \cfrac{16x^5}{4x^2}+ \cfrac{-4x^3}{4x^2} + \cfrac{-20x^2}{4x^2} \\[2ex] & = \bm{4x^3-x-5} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-868da1546d3e4d33e8226774020cbb2d_l3.png "Rendered by QuickLaTeX.com")
Lembre-se que na divisão monomial os coeficientes são divididos entre si e os expoentes das potências com base equivalente são subtraídos.
Exercício 3
Resolva a seguinte divisão de um polinômio por um monômio:
Para dividir um polinômio por um monômio você deve resolver a divisão de cada termo do polinômio pelo referido monômio:
![\begin{aligned} \left(12x^{10}-30x^7-18x^6+54x^4 \right) : \left(-6x^3\right) & = \cfrac{12x^{10}}{-6x^3}+ \cfrac{-30x^{7}}{-6x^3} + \cfrac{-18x^6}{-6x^3} + \cfrac{54x^4}{-6x^3} \\[2ex] & = \bm{-2x^7+5x^4+3x^3-9x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a8d5fe46b397f2f531a865e7cb0df3cf_l3.png "Rendered by QuickLaTeX.com")
Tenha em mente que o monômio divisor é negativo e, portanto, os sinais de todas as divisões mudam.
Exercício 4
Execute a seguinte divisão dos polinômios:
Para dividir polinômios você deve aplicar o método explicado acima:
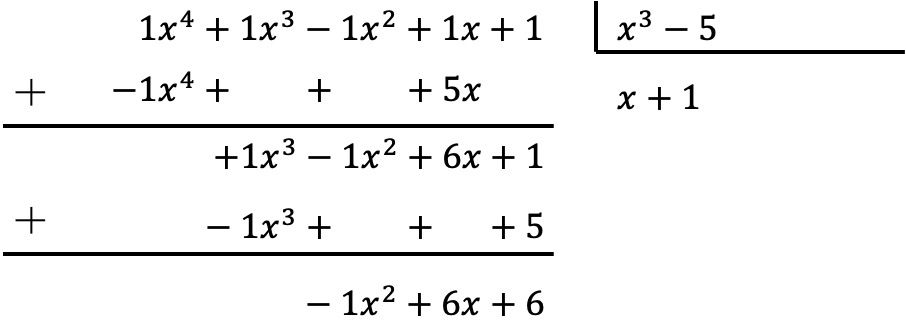
O resultado da divisão entre os dois polinômios é, portanto:
Quociente:
Descansar:
Exercício 5
Calcule a seguinte divisão de polinômios:
Para resolver a divisão do polinômio pelo binômio devemos aplicar o método que vimos acima:
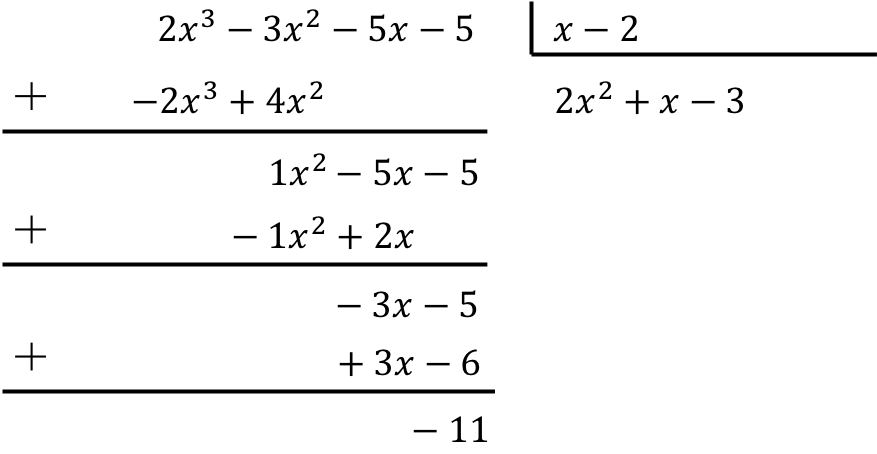
O resultado da divisão polinomial é, portanto:
Quociente:
Descansar:
Exercício 6
Resolva a seguinte divisão de polinômios:
Para calcular a divisão de polinômios, devemos aplicar o método explicado:
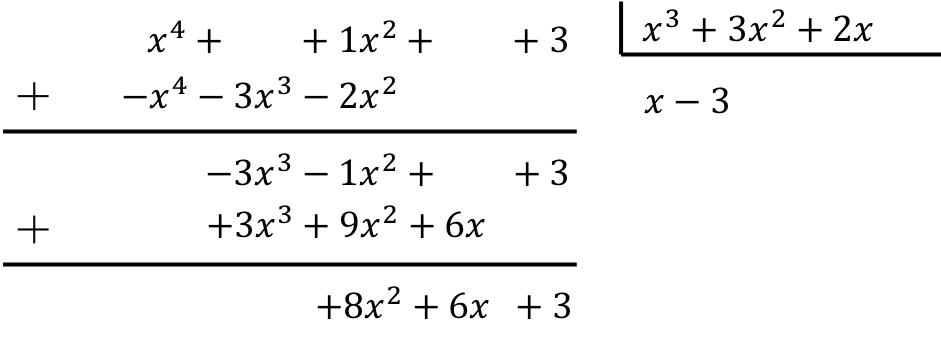
O resultado da divisão entre os dois polinômios é, portanto:
Quociente:
Descansar:
Exercício 7
Encontre o resultado da seguinte divisão entre 2 polinômios:
Para calcular a divisão do polinômio pelo trinômio deve-se aplicar o método explicado:
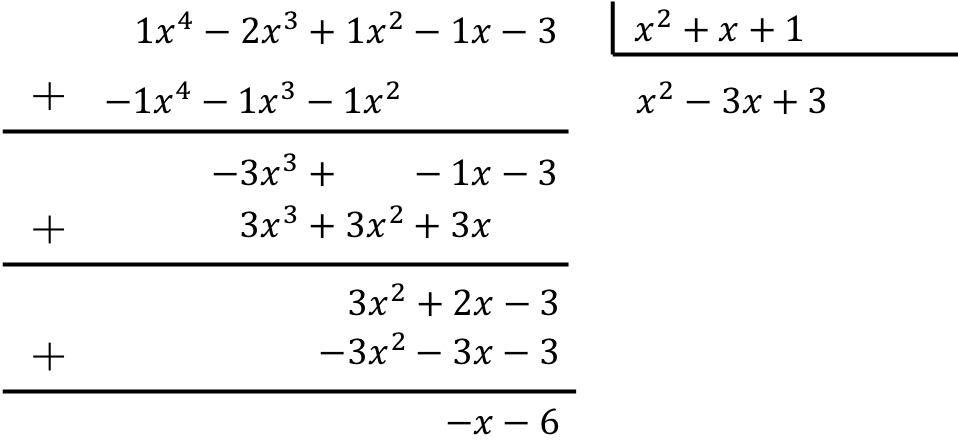
O resultado da divisão entre os dois polinômios é, portanto:
Quociente:
Descansar:
👉👉👉Se você chegou até aqui, significa que já sabe como os polinômios são divididos. Brilhante! Agora que você já domina a divisão de polinômios, saiba que existe um método que permite resolver certas divisões entre polinômios com muito mais rapidez . Esta é uma divisão sintética ou regra de Ruffini , você pode ver como esse truque é aplicado e quando pode ser usado clicando no link.😉
