Transformações de funções: Tradução, Expansão e Simetria

Esta página explica o que são transformações de função e como encontrá-las. Existem três tipos de transformações: translações (ou deslocamentos), simetrias e expansões (ou contrações). Você também encontrará exercícios resolvidos passo a passo para que possa praticar e entender os conceitos sem deixar dúvidas.

O que são transformações de função?

Às vezes, podemos ser solicitados a representar graficamente funções elementares muito semelhantes a outras que já conhecemos. Bem, em vez de representar novamente a função semelhante, podem ser usadas técnicas para passar da representação de uma função para outra de maneira fácil e rápida.

Assim, as transformações de funções são técnicas que permitem passar da representação gráfica de uma função à representação gráfica de outra função muito semelhante através de operações elementares.

Basicamente, existem três tipos de transformações de funções elementares:

Translações ou movimentos : uma função pode ser movida verticalmente e horizontalmente.
Reflexões ou simetrias : Uma função pode ser refletida usando o eixo X ou o eixo Y como eixo de simetria.
Expansões e compressões : Uma função pode ser ampliada ou reduzida.

Depois de vermos o conceito de transformação de uma função, nos aprofundaremos em cada tipo de modificação.

Translações ou movimentos de funções

Começaremos com mudanças de função. Existem dois tipos: translações verticais e translações horizontais.

Translação ou movimento vertical de uma função

Para transladar ou mover uma função verticalmente (ao longo do eixo Y), você deve adicionar ou subtrair uma constante à função:

Movemos uma função k unidades para cima adicionando ka à função:

$\bm{f(x)+k}$

Deslocamos uma função k unidades para baixo subtraindo ka da função:

$\bm{f(x)-k}$

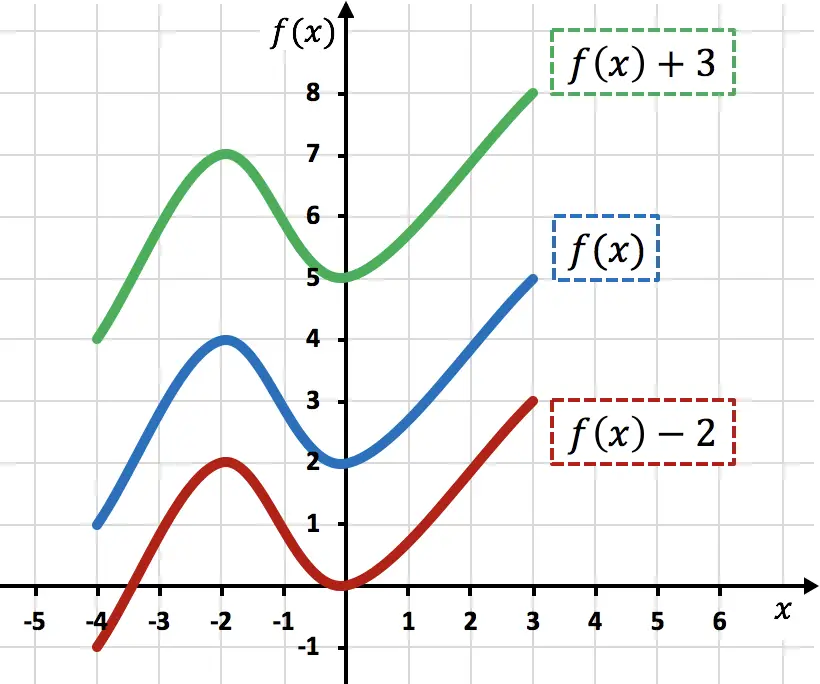
Translação ou movimento vertical de uma função

Como você pode ver no gráfico, adicionar uma constante a qualquer função desloca as unidades adicionadas para cima (função verde). Por outro lado, ao subtrair um número de uma função, as unidades subtraídas são movidas para baixo (função vermelha).

Observe que neste tipo de movimentos apenas as coordenadas Y dos pontos de função são alteradas, enquanto as coordenadas X permanecem as mesmas.

Tradução ou movimento horizontal de funções

Para transladar ou deslocar uma função horizontalmente (ao longo do eixo X), você deve adicionar ou subtrair uma constante à variável independente x :

O gráfico de

$\bm{f(x+k)}$

é o gráfico de

$f(x)$

moveu k unidades para a esquerda.

O gráfico de

$\bm{f(x-k)}$

é o gráfico de

$f(x)$

deslocou k unidades para a direita.

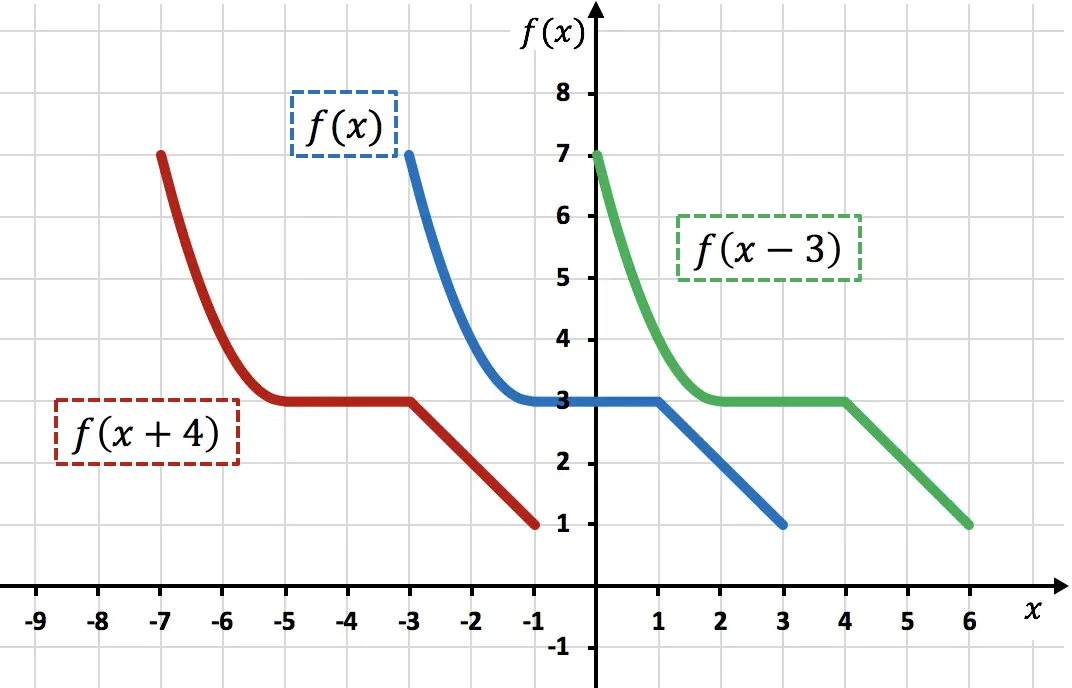
Translação ou movimento horizontal de uma função

Como você pode ver no gráfico, ao adicionar uma constante diretamente à variável x , a função desloca as unidades adicionadas para a esquerda (função vermelha). Por outro lado, ao subtrair um número da variável x , a função desloca as unidades subtraídas para a direita (função verde).

Observe que neste tipo de movimentos apenas as coordenadas X dos pontos de função são alteradas, enquanto as coordenadas Y continuam com o mesmo valor.

Exemplo de tradução ou movimentação de uma função

Mova a seguinte função 4 unidades para cima e 3 unidades para a direita:

$f(x)=x^2$

Para mover a função 4 unidades para cima, precisamos adicionar 4 unidades à função:

$f(x) + 4 = x^2 + 4$

E para também mover a função 3 unidades para a direita devemos calcular

$f(x-3)$

. Portanto, onde há um

$x$

pudermos

$x-3 :$

$f(x-3) = (x-3)^2 + 4$

A função deslocada 4 unidades para cima e 3 unidades para a direita é, portanto:

$\bm{f(x) = (x-3)^2 + 4}$

Abaixo você tem a função original e a função transformada representadas graficamente para que você possa ver a diferença entre elas:

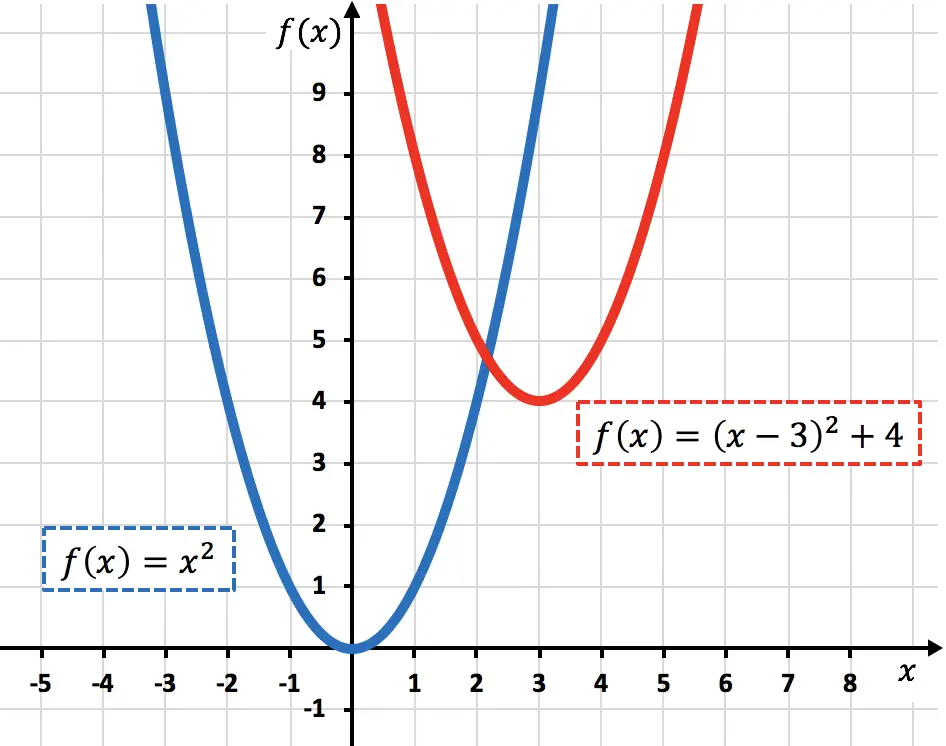
exemplo de translação ou movimento de uma função

Alguns matemáticos chamam de deslocamento oblíquo ou translação quando os dois tipos de movimento ocorrem ao mesmo tempo.

Reflexão ou simetria de uma função em relação aos eixos coordenados

Podemos representar a função simétrica em relação a qualquer eixo cartesiano da seguinte maneira:

Para refletir uma função em relação ao eixo x, precisamos alterar o sinal da função, ou seja, precisamos calcular

$\bm{-f(x)}.$

Para refletir uma função em relação ao eixo y, devemos negar a variável independente x , ou seja, devemos calcular

$\bm{f(-x)}.$

reflexão ou simetria em relação ao eixo X

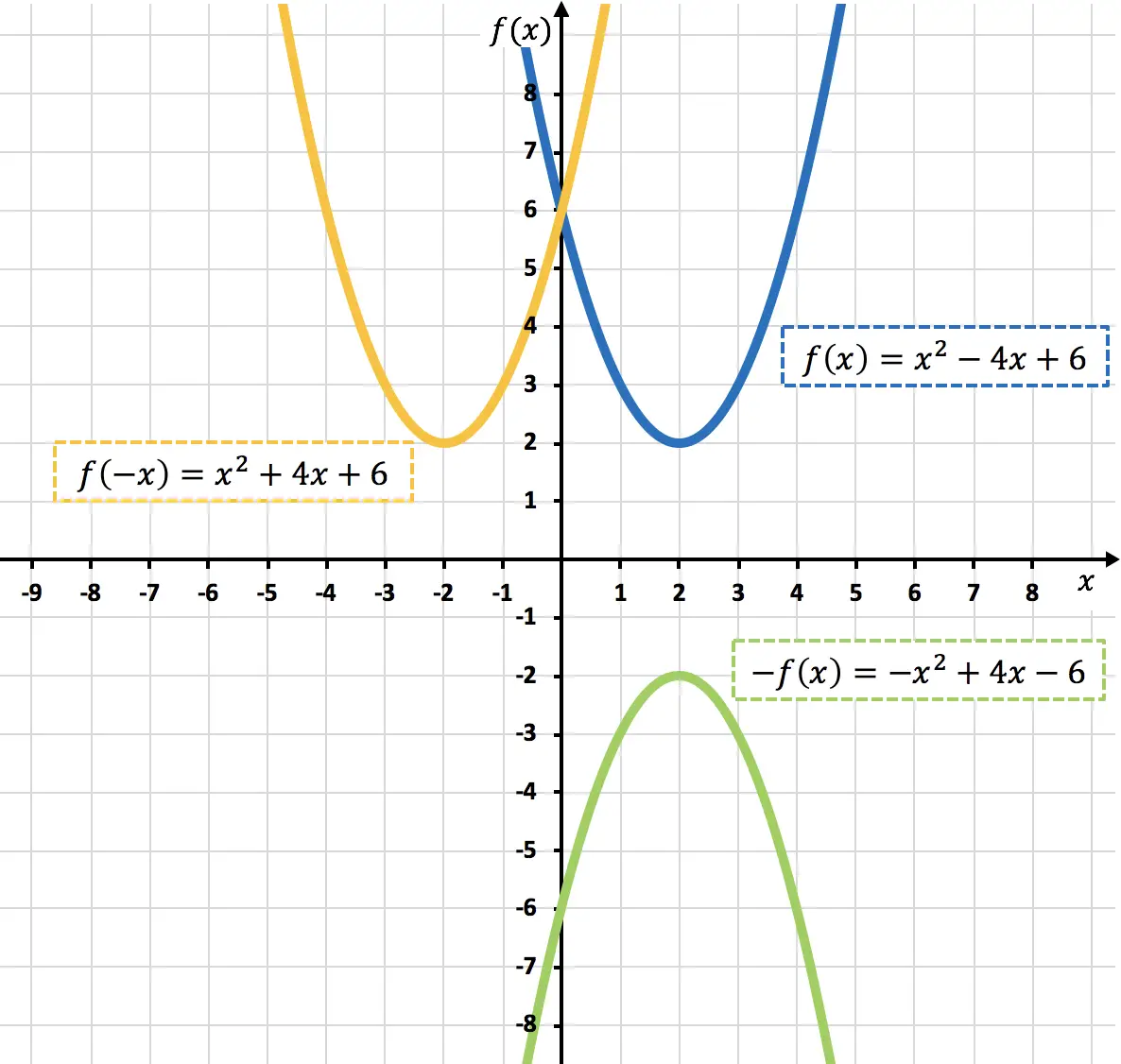
Como você pode ver no gráfico anterior, ao multiplicar uma função por -1, nós a invertemos graficamente (função laranja), ou seja, a espelhamos em relação ao eixo X.

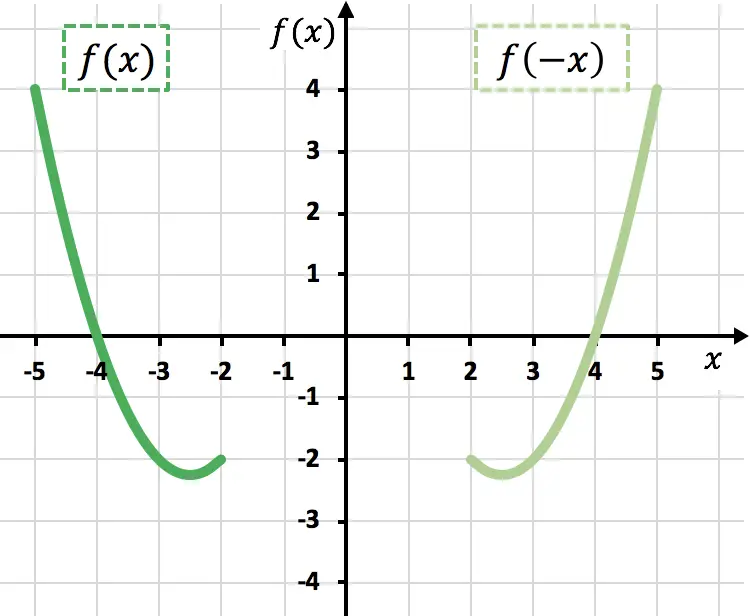
Como pode ser visto no gráfico anterior, ao negar a variável x , espelhamos a função em relação ao eixo Y (função verde claro).

Exemplo de espelhamento de uma função

Calcule a função simétrica em torno do eixo OX e a função simétrica em torno do eixo OY da seguinte função quadrática:

$f(x)=x^2-4x+6$

Para encontrar a função simétrica em relação ao eixo X, devemos fazer

$-f(x)$

$-f(x)=-\bigl[x^2-4x+6\bigr]$

$\bm{-f(x)=-x^2+4x-6}$

E para encontrar a função simétrica em relação ao eixo Y devemos fazer

$f(-x)$

. Portanto, substituímos onde há um

$x$

na função original pelo termo

$-x :$

$f(x)=x^2-4x+6$

$f(-x)=(-x)^2-4\cdot (-x)+6$

$f(-x)=x^2-4\cdot (-x)+6$

$\bm{f(-x)=x^2+4x+6}$

Abaixo você representou a função original e as funções simétricas encontradas:

exemplo de funções simétricas em relação aos eixos x e y

Expansões e contrações de função

Tal como acontece com as translações, existem dois tipos de expansões ou contrações: verticais e horizontais.

Expansão e contração vertical de uma função

Multiplicando uma função inteira por um coeficiente, podemos fazê-la expandir ou contrair:

Para expandir (ou dilatar) uma função no eixo Y, precisamos multiplicá-la por um número maior que 1:

$kf(x)\qquad k>1″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”121″ style=”vertical-align: -5px;”></p> </p> <p style=$ Para reduzir uma função no eixo Y, precisamos multiplicá-la por um número positivo menor que 1:

$kf(x)\qquad 0</div> <div class="wp-block-image"> <figure class="aligncenter size-large is-resized"><img decoding="async" loading="lazy" src="http://mathority.org/wp-content/uploads/2023/07/expansion-et-contraction-d-une-fonction.webp" alt="expansion et contraction verticales d'une fonction" class="wp-image-320" width="442" height="438" srcset="" sizes="" data-src=""></figure> </div> <p> Comme vous pouvez le voir dans le graphique précédent, si on multiplie une fonction par un coefficient supérieur à 1 (fonction verte) on la rend plus grande le long de l’axe OY, en revanche, si on multiplie une fonction par un coefficient supérieur à 0 mais plus petit que 1 (fonction rouge), nous le rendons plus petit le long de l’axe OY.</p> <h3 class="wp-block-heading"> Expansion et contraction horizontales d’une fonction</h3> <p> Dans ce cas, au lieu de multiplier la fonction entière par un coefficient, pour qu’une fonction se dilate ou se contracte horizontalement, nous devons multiplier la variable indépendante <em>x</em> . </p> <div style="padding-top: 23px; padding-bottom: 0.5px; padding-right: 30px; padding-left: 30px; border: 2px dashed #FF9B28; border-radius:20px;"> Pour <strong>étendre (ou dilater) une fonction sur l’axe X,</strong> il faut multiplier tous les <em>x</em> par un nombre compris entre 0 et 1 :” title=”Rendered by QuickLaTeX.com” height=”392″ width=”2425″ style=”vertical-align: -4px;”></p> <p> f(kx)\qquad 0</p> <p style=$ Para reduzir uma função no eixo X, precisamos multiplicar todos os x por um número maior que 1:

$f(kx)\qquad k>1″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”121″ style=”vertical-align: -5px;”></p> </p> </div> <div class=$

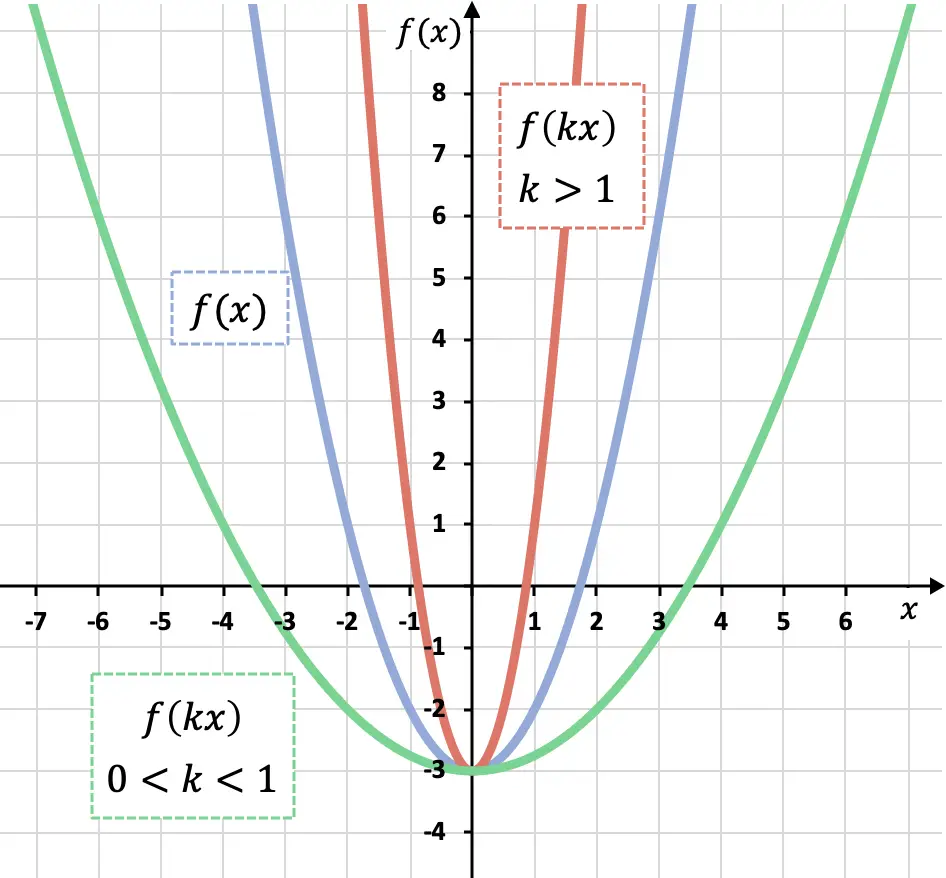
expansão ou contração horizontal de uma função

Como você pode ver no gráfico anterior, se multiplicarmos todos os x de uma função por um coeficiente maior que 0 mas menor que 1 (função verde) ampliamos ao longo do eixo OX, por outro lado, se multiplicarmos uma função por um coeficiente maior que 1 (função vermelha), reduzimos ao longo do eixo OX.

Exemplo de como expandir ou recolher uma função

Duplique a seguinte função irracional vertical e horizontalmente:

$f(x)=\sqrt{9-x^2}$

Para estender a função no eixo y por dois, devemos multiplicar a função inteira por 2:

$2f(x)=2\sqrt{9-x^2}$

E para também expandir a função por dois no eixo x, devemos multiplicar todos os x da função por

$\displaystyle \frac{1}{2}:$

$\displaystyle f\left(\frac{1}{2}x\right)=2\sqrt{9-\left(\frac{1}{2}x\right)^2}$

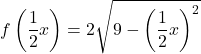
A função duplicada nos dois eixos coordenados é, portanto:

$\displaystyle\bm{f(x) = 2\sqrt{9-\left(\frac{1}{2}x\right)^2}}$

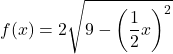
Abaixo você tem a função original e a transformada representada graficamente para que você possa ver as diferenças entre elas:

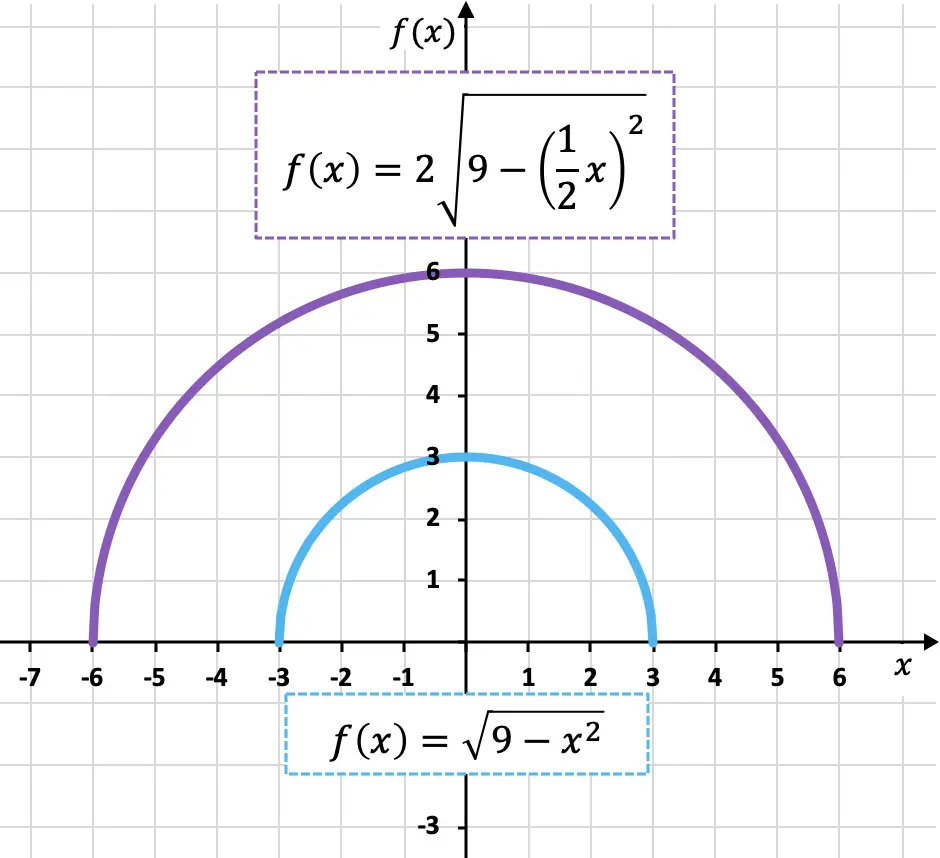
exemplo de como expandir e recolher uma função

Como você pode ver, o novo recurso (cor roxa) é duas vezes maior que o recurso original (cor azul) tanto vertical quanto horizontalmente, portanto, o recurso foi expandido.

Exercícios resolvidos sobre transformações de funções

Exercício 1

Mova a seguinte função de terceiro grau 5 unidades para cima:

$f(x) = 4x^3-9x-2$

Veja a solução

Para mover a função 5 unidades para cima, adicione 5 à função:

$\begin{aligned} f(x) + 5 & = 4x^3-9x-2 + 5 \\[2ex] & = 4x^3-9x+3 \end{aligned}$

A função deslocada em 5 unidades é, portanto:

$\bm{f(x) = 4x^3-9x+3}$

Exercício 2

Encontre a função simétrica em torno do eixo Y da seguinte função quadrática:

$f(x) = 2x^2-3x+6$

Veja a solução

Para encontrar a função simétrica em relação ao eixo Y é necessário calcular

$f(-x)$

, ou seja, precisamos substituir

$x$

Para

$-x$

na função:

$f(-x) = 2(-x)^2-3\cdot (-x)+6$

$f(-x) = 2x^2+3x+6$

A função simétrica em relação ao eixo OY é, portanto:

$\bm{f(x) = 2x^2+3x+6}$

Exercício 3

Execute uma compressão horizontal da seguinte função para um terço de sua representação:

$f(x) = x^3-4x^2-5x+1$

Veja a solução

Para reduzir uma função através do

$f(3x) = (3x)^3-4(3x)^2-5(3x)+1$

$f(3x) = 27x^3-4\cdot 9 x^2-15x+1$

$f(3x) = 27x^3-36 x^2-15x+1$

A função reduzida é portanto:

$\bm{f(x) = 27x^3-36 x^2-15x+1}$

Exercício 4

Calcule a função simétrica em relação ao eixo OX da seguinte função transladada 4 unidades para a direita:

$f(x) = 3x^3-x^2+5x+8$

Veja a solução

Antes de calcular a função simétrica, devemos primeiro mover a função 4 unidades para a direita, portanto:

$f(x-4) = 3(x-4)^3-(x-4)^2+5(x-4)+8$

$f(x-4) = 3(x-4)^3-(x-4)^2+5x-20+8$

$f(x-4) = 3(x-4)^3-(x-4)^2+5x-12$

E depois de movermos a função, calculamos a função simétrica em relação ao eixo X. Para fazer isso, devemos negar a função obtida:

$\displaystyle -f(x) = -\Bigl[3(x-4)^3-(x-4)^2+5x-12\Bigr]$

$-f(x) = -3(x-4)^3+(x-4)^2-5x+12$

Resumindo, a função após aplicar todas as operações elementares é:

$\bm{f(x) =-3(x-4)^3+(x-4)^2-5x+12}$

Exercício 5

Desloque a seguinte função 2 unidades para a esquerda e expanda-a verticalmente por um fator de 4:

$f(x) = x^4-5x^3-x-3$

Veja a solução

Primeiro, movemos a função duas unidades para a esquerda:

$f(x+2) = (x+2)^4-5(x+2)^3-(x+2)-3$

$f(x-4) = (x+2)^4-5(x+2)^3-x-2-3$

$f(x-4) = (x+2)^4-5(x+2)^3-x-5$

E então expandimos a função ao longo do eixo Y com um fator de 4:

$4\cdot f(x) = 4\cdot \Bigl[(x+2)^4-5(x+2)^3-x-5\Bigr]$

$f(x) = 4(x+2)^4-20(x+2)^3-4x-20$

Concluindo, a função após aplicar todas as transformações elementares é:

$\bm{f(x) =4(x+2)^4-20(x+2)^3-4x-20}$

Exercício 6

Da função

$f(x)=x,$

determinar qual das representações no gráfico corresponde à função

$f(x)=x-3 .$

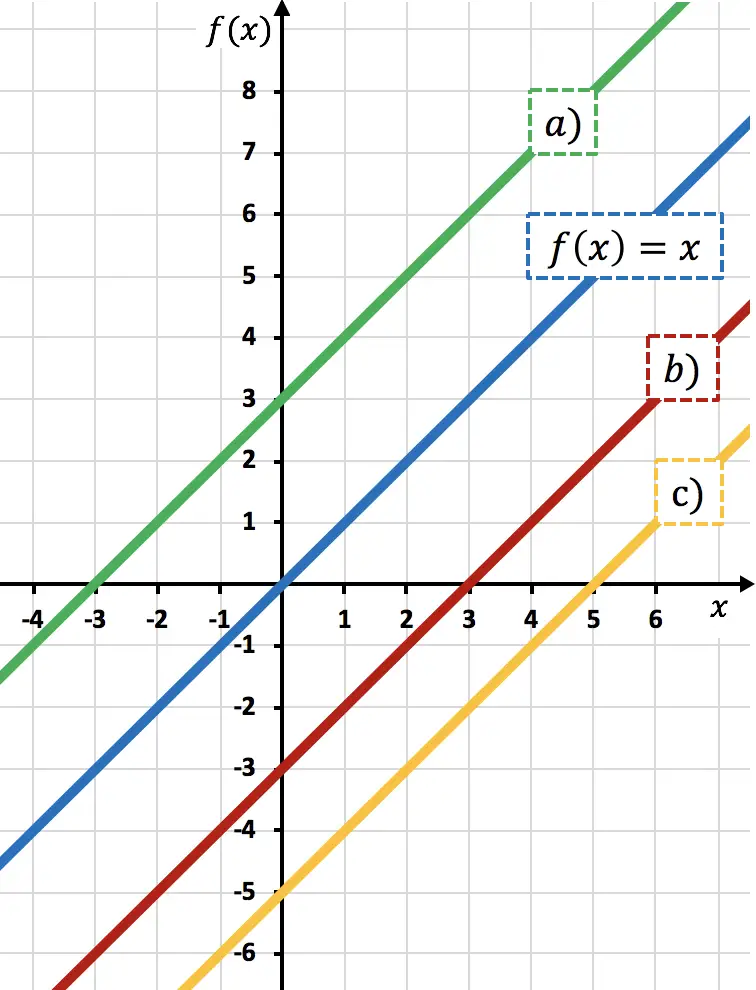
exercícios resolvidos passo a passo sobre transformações de funções

Veja a solução

Função

$f(x)=x-3$

é a função

$f(x)=x$

moveu 3 unidades para baixo. Porque ao subtrair um número de uma função, você move a função para baixo.

Portanto, a representação de

$f(x)=x-3$

corresponde à linha b) , porque está deslocada 3 unidades para baixo em comparação com

$f(x)=x .$

Isto pode ser visto olhando para o eixo vertical: quando

$f(x)=x$

passa por 0, a linha vermelha passa por -3, então é deslocada 3 unidades para baixo.

Exercício 7

Da função

$f(x)=x^2+2,$

determine qual parábola é a representação da função

$f(x)=(x-6)^2+2 .$

Veja a solução

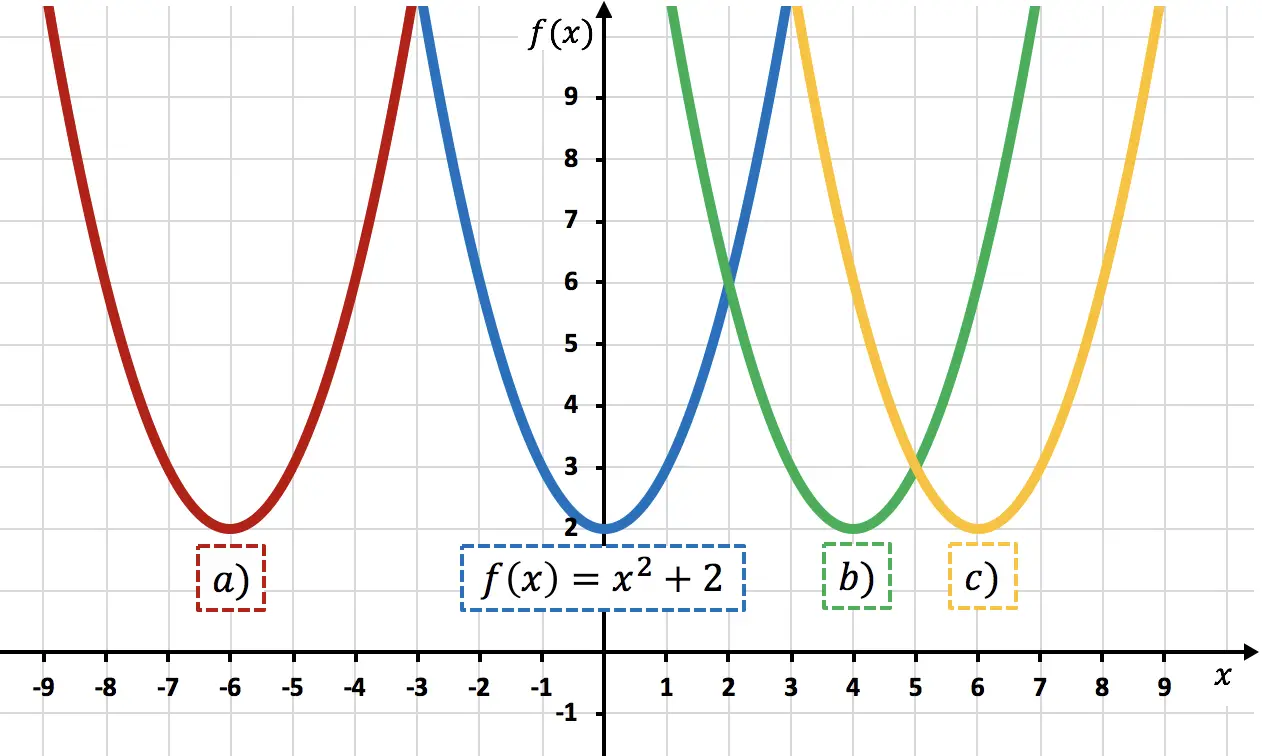
Função

$f(x)=(x-6)^2+2$

é a função

$f(x)=x^2+2$

moveu 6 unidades para a direita. Podemos verificar isso calculando

$f(x-6):$

$f(x)=x^2+2$

$f(x-6)=(x-6)^2+2$

Portanto, a representação de

$f(x)=(x-6)^2+2$

corresponde à parábola c) , porque está deslocada 6 unidades para a direita em comparação com

$f(x)=x^2+2$

Isso pode ser visto observando os vértices das parábolas: a distância entre o vértice da parábola

$f(x)=x^2+2$

e o vértice da parábola c) tem 6 unidades, então o último é deslocado 6 unidades para a direita em comparação com o primeiro.

Transformações de funções: translações, simetria, expansão e compressão

O que são transformações de função?

Translações ou movimentos de funções

Translação ou movimento vertical de uma função

Tradução ou movimento horizontal de funções

Exemplo de tradução ou movimentação de uma função

Reflexão ou simetria de uma função em relação aos eixos coordenados

Exemplo de espelhamento de uma função

Expansões e contrações de função

Expansão e contração vertical de uma função

Exemplo de como expandir ou recolher uma função

Exercícios resolvidos sobre transformações de funções

Exercício 1

Exercício 2

Exercício 3

Exercício 4

Exercício 5

Exercício 6

Exercício 7

Deixe um comentário Cancelar resposta