Distância entre um ponto e uma reta

Aqui você encontrará a fórmula usada para calcular a distância entre um ponto e uma linha. Além disso, você poderá ver diversos exemplos e exercícios resolvidos de distâncias entre pontos e retas e, ainda, as aplicações que esta operação possui (por exemplo, encontrar a distância entre retas paralelas).

Fórmula para a distância entre um ponto e uma linha

A distância entre um ponto e uma linha é a distância mais curta entre esse ponto e a linha. Matematicamente, esta distância mínima equivale ao comprimento do segmento traçado do ponto à reta e que é perpendicular à reta.

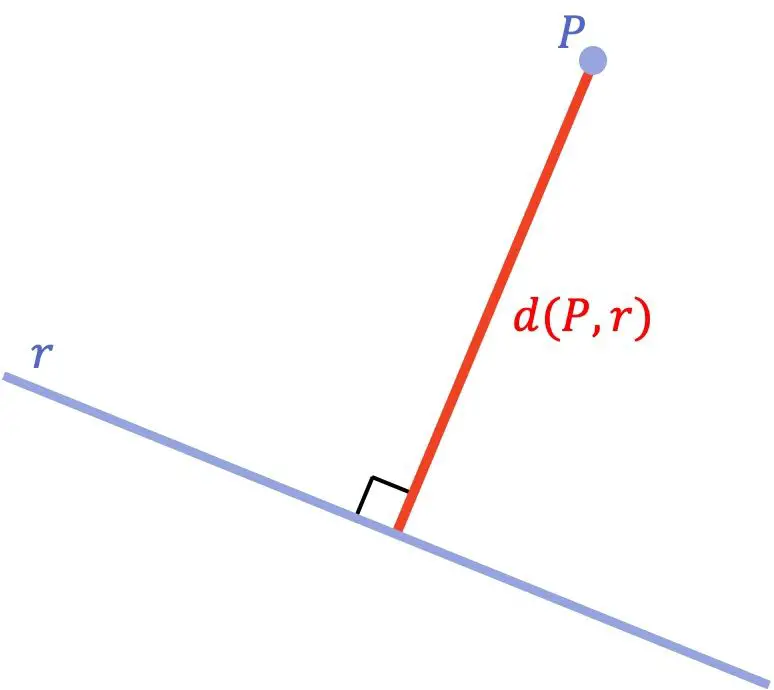
qual é a distância entre um ponto e uma reta

Depois de vermos o conceito geométrico de distância entre um ponto e uma reta, vamos ver qual é a fórmula usada para calcular essa distância:

Dada a equação implícita (ou geral) de uma reta e as coordenadas de qualquer ponto de um plano:

$r: \ Ax+By+C=0 \qquad \qquad P(p_x,p_y)$

A fórmula para a distância entre um ponto e uma linha é:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Importante: Observe que a equação da reta na fórmula está na forma de uma equação implícita (ou geral), portanto se tivermos a reta expressa em outro tipo de equação, precisamos passá-la primeiro para sua equação implícita e depois podemos aplicar a fórmula.

Exemplo de cálculo da distância entre um ponto e uma linha

Abaixo você pode ver um exemplo de cálculo da distância entre um ponto e uma linha:

Encontre a distância entre o ponto
$P$

e a lei

$r:$

$P(2,-1) \qquad \qquad r: \ 3x+4y-5=0$

Para calcular a distância entre o ponto e a reta, basta aplicar sua fórmula:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Agora substituímos cada termo pelo seu valor:

$d(P,r)= \cfrac{\lvert 3\cdot 2 + 4\cdot (-1)-5\rvert}{\sqrt{3^2+4^2}}$

E finalmente calculamos a distância:

$d(P,r)= \cfrac{\lvert 6 -4-5\rvert}{\sqrt{9+16}} =\cfrac{\lvert -3 \rvert}{\sqrt{25}} = \mathbf{\cfrac{3}{5}}$

Distância entre duas linhas paralelas

Uma das aplicações do cálculo da distância entre uma reta e um ponto é encontrar a distância entre retas paralelas.

Obviamente, para entender o conceito que explicaremos a seguir, você deve saber o que são retas paralelas , então se você não sabe exatamente sua definição, deixamos um link onde explicamos detalhadamente e você também poderá ver exemplos de linhas paralelas.

Para encontrar a distância entre duas retas paralelas, basta pegar um ponto em uma das duas retas e calcular a distância desse ponto até a outra reta.

Assim, para determinar a distância entre duas retas paralelas, também é utilizada a fórmula da distância entre uma reta e um ponto.

Por outro lado, se ao usar a fórmula obtivermos uma distância de 0 unidades, isso significa que as retas se tocam em algum ponto e, portanto, as retas não são paralelas, mas se cruzam, coincidentes ou perpendiculares. Se quiser, você pode conferir as diferenças entre esse tipo de linha em nosso site.

Então vamos ver como resolver um problema de distância entre duas retas paralelas através de um exemplo:

Encontre a distância entre as duas linhas paralelas a seguir:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

A primeira coisa que precisamos fazer é marcar um ponto em uma das linhas (a que você deseja). Neste caso, calcularemos um ponto na reta

$s.$

Para fazer isso, você deve atribuir um valor a uma das variáveis, por exemplo faremos

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

E agora limpamos a outra variável (

$y$

) da equação obtida para saber quanto vale neste momento:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

Portanto, o ponto obtido da reta

$s$

Leste:

$P(0,-2)$

E como já temos um ponto em uma reta, calculamos a distância desse ponto até a outra reta usando a fórmula:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{2}{\sqrt{20}}=\bm{0,45}$

Problemas resolvidos de distância entre um ponto e uma linha

Exercício 1

Calcular a distância entre o ponto

$P$

e a lei

$r:$

$P(4,2) \qquad \qquad r: \ 5x-3y+6=0$

veja solução

Para encontrar a distância entre um ponto e uma reta, basta aplicar sua fórmula:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Substituímos cada termo pelo seu valor e calculamos a distância:

$d(P,r)= \cfrac{\lvert 5\cdot 4 + (-3)\cdot 2+6\rvert}{\sqrt{5^2+(-3)^2}}=\cfrac{20}{\sqrt{34}}= \bm{3,43}$

Exercício 2

Qual é a distância entre o ponto

$P$

e a lei

$r$

$P(-3,-1) \qquad \qquad r: \ y=-3x+5$

veja solução

Neste caso, a equação da reta está na forma implícita (ou geral). Em vez disso, para usar a fórmula da distância de um ponto a uma reta, a reta deve ser expressa como uma equação implícita. Devemos, portanto, primeiro transformar a reta e passá-la para uma equação implícita (basta passar todos os termos do mesmo lado da equação):

$r: \ 3x+y-5=0$

E uma vez que a reta já está na forma explícita, podemos agora usar a fórmula para a distância entre um ponto e uma reta:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Portanto, substituímos cada termo pelo seu valor e calculamos a distância:

$d(P,r)= \cfrac{\lvert 3\cdot (-3) + 1\cdot (-1)-5\rvert}{\sqrt{3^2+1^2}}=\cfrac{\lvert -9-1-5\rvert}{\sqrt{9+1}}=\cfrac{15}{\sqrt{10}}= \bm{4,74}$

Exercício 3

Qual é a distância entre as duas linhas a seguir?

$r: \ x+3y-4=0 \qquad \qquad s: \ 2x+6y+6=0$

veja solução

Primeiro, verificaremos se se trata de duas retas paralelas. Para isso, os coeficientes das variáveis

$x$

$y$

devem ser proporcionais entre si, mas não aos termos independentes:

$\cfrac{1}{2} = \cfrac{3}{6}\neq \cfrac{-4}{6} \ \longrightarrow \ \text{Paralelas}$

Na verdade, as linhas são paralelas, podemos, portanto, aplicar o procedimento.

Agora precisamos pegar um ponto de uma das retas (a que você deseja). Neste caso, calcularemos um ponto na reta

$s.$

Para fazer isso, você deve atribuir um valor a uma das variáveis, por exemplo faremos

$x=0:$

$2x+6y+6=0 \ \xrightarrow{x \ = \ 0} \ 2\cdot 0+6y+6=0$

E agora limpamos a outra variável (

$y$

) da equação obtida para saber seu valor neste ponto:

$6y=-6$

$y= \cfrac{-6}{6}$

$y= -1$

Para que o ponto obtido da reta

$s$

Leste:

$P(0,-1)$

Depois de conhecermos um ponto em uma reta, calculamos a distância desse ponto até a outra reta com a fórmula:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 1\cdot 0 + 3\cdot (-1) +(-4)\rvert}{\sqrt{1^2+3^2}}= \cfrac{7}{\sqrt{10}}=\bm{2,21}$

Exercício 4

Calcule o valor da incógnita

$k$

de modo que a distância entre o ponto

$P$

e a lei

$r$

ou seja, 5 unidades.

$P(-2,5) \qquad \qquad r: \ 12x-5y+k=0$

veja solução

Devemos primeiro aplicar a fórmula para a distância entre um ponto e uma reta:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Agora substituímos cada termo pelo seu valor e simplificamos a expressão:

$d(P,r)= \cfrac{\lvert 12\cdot (-2) + (-5)\cdot 5+k\rvert}{\sqrt{12^2+(-5)^2}}= \cfrac{\lvert -24-25+k\rvert}{\sqrt{169}}=\cfrac{\lvert -49+k\rvert}{13}$

O enunciado do problema nos diz que a distância entre o ponto e a reta deve ser igual a 5, então igualamos a expressão anterior a 5:

$\cfrac{\lvert -49+k\rvert}{13}=5$

E resolvemos a equação resultante. No numerador da fração existe um valor absoluto, portanto, devemos analisar separadamente quando o valor absoluto é positivo e quando é negativo:

$\cfrac{+(-49+k)}{13}=5$