Distância entre duas linhas no espaço (em R3)

Nesta página você descobrirá como é calculada a distância entre duas retas no espaço (em R3), qualquer que seja o seu tipo (retas paralelas, secantes, coincidentes, secantes, perpendiculares, etc.). Além disso, você poderá ver exemplos e exercícios resolvidos passo a passo.

Como calcular a distância entre duas linhas

A distância entre duas linhas é a distância mínima entre qualquer ponto de uma linha e qualquer ponto da outra linha. Esta distância corresponde ao comprimento do segmento que vai de uma reta a outra reta e que, ao mesmo tempo, é perpendicular a ambas as retas.

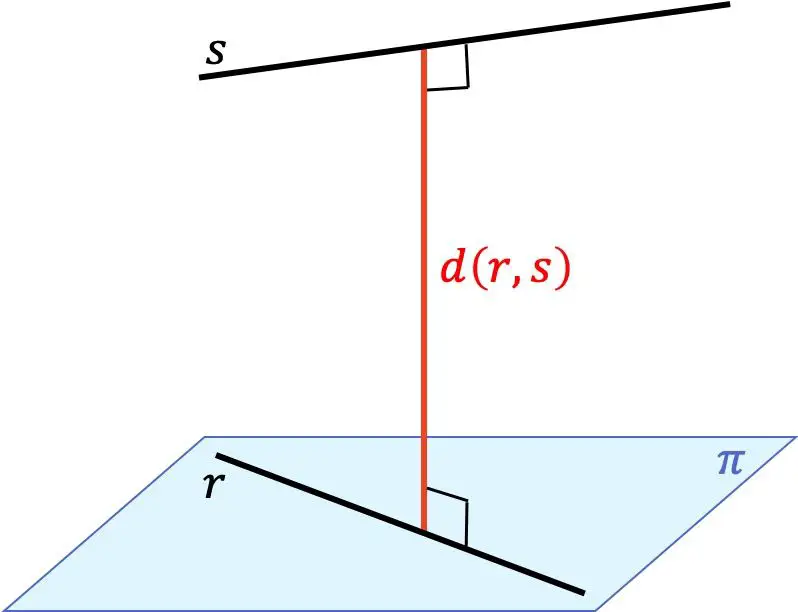
distância entre duas linhas no espaço (em R3)

Portanto, encontrar a distância entre duas linhas diferentes no espaço tridimensional (3D) depende da posição relativa entre elas:

Se as duas retas coincidem ou se cruzam , a distância entre as duas retas é zero, porque elas se cruzam (pelo menos) em um ponto.
Quando as duas retas são paralelas , precisamos pegar qualquer ponto de uma das retas e calcular a distância entre esse ponto e a outra reta (abaixo você tem um exemplo de como fazer isso).
Se as duas linhas se cruzam no espaço, precisamos aplicar a fórmula para a distância entre duas linhas que se cruzam (veja abaixo uma explicação detalhada).

Portanto, para calcular a distância entre duas retas, primeiro você deve saber que tipo de reta são e depois, dependendo do caso, usar uma fórmula ou outra. Portanto, é importante que você já domine como encontrar a posição relativa de duas linhas no espaço antes de continuar, mas se não lembra como foi feito no link verá uma explicação bem completa além de exemplos e exercícios resolvidos passo a passo.

Como encontrar a distância entre duas linhas paralelas no espaço

O cálculo da distância entre duas retas paralelas no espaço (em R3) é feito da mesma forma que no plano (em R2): você deve pegar um ponto em qualquer uma das duas retas e encontrar a distância desse ponto na outra linha.

Assim, a fórmula para calcular a distância de um ponto a uma reta em 3 dimensões (e que é usada para determinar a distância entre duas retas paralelas) é:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}$

Ouro:

$\lvert \vv{\text{v}}_r \rvert$

é a magnitude do vetor de direção da linha

$r.$
$Q$

é um ponto na linha

$r,$

$P$

um ponto na linha

$s$

E

$\vv{QP}$

o vetor definido pelos dois pontos
$\lvert \vv{QP} \times \vv{\text{v}}_r \rvert$

é a magnitude do produto vetorial entre os vetores

$\vv{QP}$

E

$\vv{\text{v}}_r$

Como exemplo, vamos resolver um problema de distância entre 2 retas paralelas no espaço:

Qual é a distância entre as duas linhas paralelas a seguir?

$r: \ (x,y,z) = (2,1,1) + t(-1,3,2)$

$s: \ (x,y,z) = (-2,4,1) + t(2,-6,-4)$

Ambas as retas são expressas na forma de uma equação vetorial, portanto, podemos facilmente descobrir o vetor diretor e um ponto de cada uma delas:

$\displaystyle r : \ \begin{cases}\vv{\text{v}}_r=(-1,3,2) \\[1.7ex] Q(2,1,1) \end{cases} \qquad \qquad s: \ \begin{cases}\vv{\text{v}}_s=(2,-6,-4) \\[1.7ex] P(-2,4,1) \end{cases}$

Se você tiver alguma dúvida sobre como determinar o vetor diretor e um ponto de uma reta, recomendamos que você dê uma olhada na explicação da equação da reta . Lá explicamos isso para todas as equações da reta, pois encontrar o vetor diretor e um ponto que pertence a uma reta depende do tipo de equação em que a reta é expressa.

Agora, para encontrar a distância entre as duas retas paralelas, precisamos aplicar a fórmula da distância de um ponto a uma reta:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}$

Então por um lado calculamos o módulo do vetor resultante do produto vetorial. Se tiver dúvidas sobre como é calculado, pode consultar a fórmula do produto vetorial , onde, além disso, poderá ver exemplos e exercícios resolvidos desta operação entre vetores.

$\vv{QP} = Q - P = (2,1,1)-(-2,4,1) = (4,-3,0)$

$\vv{QP} \times \vv{\text{v}}_r =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 4&-3&0 \\[1.1ex] -1&3&2 \end{vmatrix}=-6\vv{i} -8\vv{j}+9\vv{k}$

$\left|\vv{QP} \times \vv{\text{v}}_r \right| =\sqrt{(-6)^2+(-8)^2+9^2} = \sqrt{36+64+81} = \sqrt{181}$

E, por outro lado, encontramos a magnitude do vetor da reta

$r:$

$\lvert \vv{\text{v}}_r \rvert = \sqrt{(-1)^2+3^2+2^2} = \sqrt{1+9+4} = \sqrt{14}$

Por fim, substituímos o valor de cada termo na fórmula e calculamos a distância entre as linhas:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}=\cfrac{\sqrt{181}}{\sqrt{14}} = \bm{3,60}$

Portanto, a distância entre as duas linhas é de 3,60 unidades.

Como determinar a distância entre duas linhas que se cruzam no espaço

Como vimos no início, o método para determinar a distância entre duas retas que se cruzam é diferente do procedimento para distâncias entre retas paralelas.

distância entre linhas cruzadas no espaço

Assim, existem vários métodos para determinar a distância entre duas linhas que se cruzam no espaço. Nesta página explicaremos apenas um procedimento, o mais simples, pois os outros dois métodos são mais longos e complicados, aliás, praticamente não são utilizados.

Seja o vetor de direção e qualquer ponto de duas linhas que se cruzam:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}$

A fórmula para a distância entre duas linhas que se cruzam é:

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}$

Ouro

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|$

é o valor absoluto do produto misto dos vetores

$\vv{\text{u}}, \vv{\text{v}}$

e o vetor definido pelos pontos

$A$

$B$

. E por outro lado,

$\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert$

é a amplitude do produto vetorial entre os vetores de direção das duas linhas cruzadas.

Para que você veja como determinar a distância entre duas linhas cruzadas, resolveremos um problema como exemplo:

Qual é a distância entre as próximas duas linhas que se cruzam?

$r: \ \cfrac{x-1}{2} = \cfrac{y-2}{4} = \cfrac{z+2}{-1}$

$s: \ \cfrac{x-3}{1} = \cfrac{y+1}{3} = \cfrac{z-1}{-2}$

Primeiro, precisamos identificar o vetor diretor e um ponto em cada reta. As duas retas são expressas na forma de uma equação contínua, portanto:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} =(2,4,-1) \\[2ex] A(1,2,-2) \end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}}=(1,3,-2) \\[2ex] B(3,-1,1)\end{cases}$

E agora aplicamos a fórmula para a distância entre duas linhas que se cruzam:

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}$

Por um lado resolvemos o produto misto (ou produto escalar triplo):

$\vv{AB} = B - A = (3,-1,1) - (1,2,-2) = (2,-3,3)$

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| =\left| \begin{vmatrix} 2&4&-1 \\[1.1ex] 1&3&-2 \\[1.1ex] 2&-3&3 \end{vmatrix}\right| = \left| -13 \right| =13$

E, por outro lado, encontramos o módulo do produto vetorial (ou produto vetorial):

$\vv{\text{u}} \times \vv{\text{v}} =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 2&4&-1 \\[1.1ex] 1&3&-2 \end{vmatrix}=-5\vv{i} +3\vv{j}+2\vv{k}$

$\left| \vv{\text{u}} \times \vv{\text{v}} \right| =\sqrt{5^2+3^2+2^2} = \sqrt{25+9+4} = \sqrt{38}$

Por fim, substituímos o valor de cada termo na fórmula pela distância entre duas linhas cruzadas:

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} = \cfrac{13}{\sqrt{38}}= \bm{2,11}$

Distância entre duas linhas no espaço (em r3)

Como calcular a distância entre duas linhas

Como encontrar a distância entre duas linhas paralelas no espaço

Como determinar a distância entre duas linhas que se cruzam no espaço

Deixe um comentário Cancelar resposta