Distância de uma linha a um plano no espaço

Aqui você descobrirá como se calcula a distância de uma reta a um plano e, além disso, poderá ver exemplos e exercícios resolvidos passo a passo.

Qual é a distância entre uma linha e um plano?

Na geometria analítica, a distância entre uma linha e um plano no espaço depende da posição relativa entre estes dois elementos geométricos:

Se a reta estiver incluída no plano ou se a reta e o plano forem paralelos , a distância que os separa é zero.
Se a reta for paralela ao plano , a distância da reta ao plano é encontrada tomando qualquer ponto da reta e calculando a distância desse ponto ao plano.

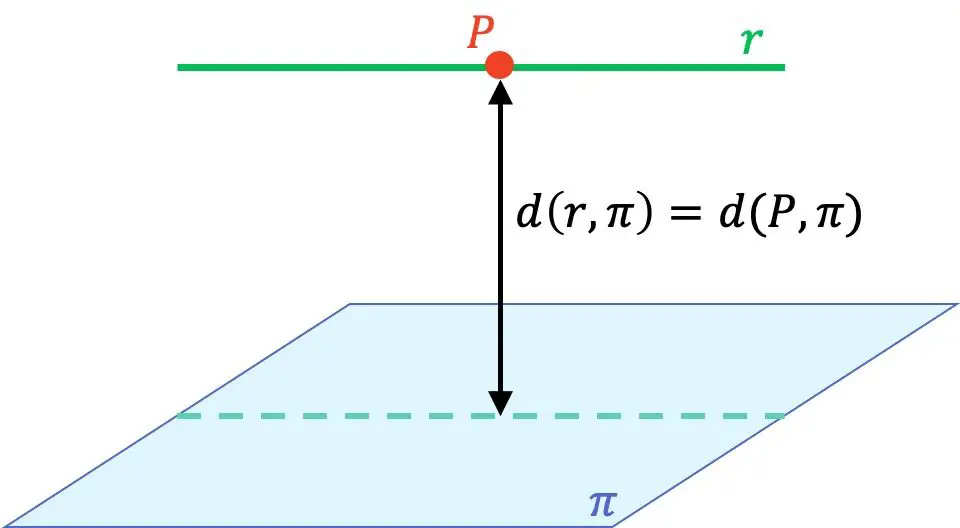
distância de uma linha a um plano no espaço

Portanto, para calcular a distância de uma reta a um plano, é essencial que você saiba determinar a posição relativa entre uma reta e um plano e como calcular a distância entre um ponto e um plano . Portanto, se você não tem total clareza ou não conhece as fórmulas, recomendamos que primeiro dê uma olhada nas páginas vinculadas, onde encontrará explicações, exemplos e exercícios resolvidos passo a passo.

Exemplo de cálculo da distância entre uma linha e um plano

Para que você veja como encontrar a distância entre uma reta e um plano no espaço (em R3), resolveremos um problema como exemplo:

Quão longe está a linha
$r$

no avião

$\pi$

?

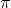
$\displaystyle r: \ \begin{cases}x=-2+t \\[1.7ex] y=1-3t \\[1.7ex] z=-1+2t\end{cases}$

$\pi : \ 4x+2y+z-6=0$

Para encontrar a distância entre a linha e o plano, primeiro você deve saber a posição relativa entre os dois.

Por um lado, a reta é definida na forma de equações paramétricas, portanto seu vetor diretor e um ponto por onde passa são:

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(1,-3,2) \\[2ex] P(-2,1,-1) \end{cases}$

E, por outro lado, o vetor normal ao plano é:

$\vv{n} =(4,2,1)$

Assim, para determinar a posição relativa entre o plano e a reta, é necessário calcular o produto escalar entre o vetor diretor da reta e o vetor normal ao plano:

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (1,-3,2) \cdot (4,2,1) \\[2ex] & = 1 \cdot 4-3 \cdot 2 +2\cdot 1 \\[2ex] &= 4 -6 +2 \\[2ex] & = 0\end{aligned}$

O resultado do produto escalar é zero, então a reta só pode estar contida no plano ou ser paralela a ele. Então, para descobrir qual é o caso, substituímos as coordenadas cartesianas do ponto da reta na equação do plano:

$4x+2y+z-6=0 \ \xrightarrow{P(-2,1,-1)} \ 4\cdot (-2) +2\cdot 1 -1-6= 0$

$-8+2-1-6 = 0$

$-13 \neq 0$

Substituindo o ponto da reta na equação do plano obtemos uma desigualdade, pois o ponto não respeita a equação do plano e, conseqüentemente, a reta e o plano são paralelos.

Uma vez que sabemos que a reta e o plano são paralelos, podemos agora calcular a distância geométrica entre eles. Para fazer isso, pegamos o ponto da reta e calculamos a distância desse ponto ao plano.

$P(-2,1,-1) \qquad \qquad \pi: \ 4x+2y+z-6=0$

Então, usamos a fórmula para a distância de um ponto a um plano:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Agora substituímos o valor de cada incógnita na fórmula:

$d(P,\pi) = \cfrac{\lvert 4\cdot (-2)+2\cdot 1+1\cdot (-1)-6\rvert}{\sqrt{4^2+2^2+1^2}}$

E, por fim, realizamos as operações:

$d(P,\pi) = \cfrac{\lvert -8+2-1-6\rvert}{\sqrt{16+4+1}}$

$d(P,\pi) = \cfrac{\lvert -13\rvert}{\sqrt{21}}$

$d(P,\pi) = \cfrac{13}{\sqrt{21}}$

Para que a distância entre a reta e o plano seja equivalente à distância entre o ponto e o plano calculada:

$\bm{d(r,\pi)=d(P,\pi) = }\cfrac{\bm{13}}{\bm{\sqrt{21}}}$

Obviamente, a distância deve sempre dar-nos um valor positivo, porque as distâncias são sempre positivas. Se obtivermos um resultado negativo, significa que cometemos um erro ao dar um passo.

Qual é a distância entre uma linha e um plano?

Exemplo de cálculo da distância entre uma linha e um plano

Deixe um comentário Cancelar resposta