Distância de um ponto a um plano no espaço (fórmula)

Nesta página você descobrirá como é calculada a distância entre um ponto e um plano no espaço (fórmula). Além disso, você poderá ver exemplos e praticar com exercícios resolvidos passo a passo.

Qual é a distância de um ponto a um plano?

Na geometria analítica, a distância de um ponto a um plano é a distância mais curta entre o ponto e qualquer outro ponto do plano. Esta distância corresponde ao comprimento do segmento perpendicular ao plano que vai do ponto ao plano.

Fórmula para a distância de um ponto a um plano

Depois de vermos exatamente a noção de distância entre um ponto e um plano, vejamos agora a fórmula para calcular essa distância:

Dado um ponto e a equação geral (ou implícita) de um plano:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

A fórmula para a distância de um ponto a um plano é:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

A prova da fórmula da distância de um ponto a um plano é bastante tediosa e longa, por isso não a faremos nesta página.

Por outro lado, se ao aplicar a fórmula obtivermos um resultado igual a zero, isso obviamente significa que a distância entre o ponto e o plano é zero e, portanto, o ponto faz parte desse plano.

Por fim, observe que para aplicar a fórmula, o plano deve ser definido como uma equação geral (ou implícita). Portanto, se fosse expresso por outro tipo de equação plana, primeiro teríamos que transformá-lo numa equação geral e depois utilizar a fórmula.

Exemplo de cálculo da distância de um ponto a um plano

Para que você possa ver como a distância entre um ponto e um plano é determinada numericamente, resolveremos um exemplo abaixo:

Calcule a distância entre o ponto P e o plano π. Tendo dito ponto e plano:

$P(1,3,-2) \qquad \qquad \pi: \ 2x+5y-4z+7=0$

Para encontrar a distância do ponto ao plano, basta aplicar a fórmula vista na seção acima:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Agora substituímos o valor de cada incógnita na fórmula:

$d(P,\pi) = \cfrac{\lvert 2\cdot 1+5\cdot 3-4\cdot (-2)+7\rvert}{\sqrt{2^2+5^2+(-4)^2}}$

E, por fim, fazemos as operações:

$d(P,\pi) = \cfrac{\lvert 2+15+8+7\rvert}{\sqrt{4+25+16}}$

$\bm{d(P,\pi) = }\cfrac{\bm{32}}{\bm{\sqrt{45}}}$

Observe que no numerador da fração existe um valor absoluto e no denominador temos uma raiz quadrada, portanto o resultado deve ser sempre positivo. Isto faz sentido porque as distâncias não podem ser negativas, mas são sempre positivas.

Calcule a distância entre dois planos paralelos

Dois planos paralelos estão sempre à mesma distância, portanto, para determinar a distância entre dois planos paralelos, podemos pegar num ponto num dos dois planos e calcular a distância desse ponto ao outro plano.

É um método para encontrar a distância entre dois planos paralelos. Porém, existe uma maneira ainda mais simples de fazer isso quando os coeficientes A, B e C das equações dos dois planos coincidem:

Considere as equações gerais (ou implícitas) de dois planos paralelos:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

A fórmula para calcular a distância entre dois planos paralelos é:

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

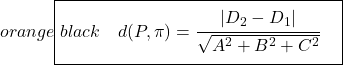
Então com certeza é mais fácil encontrar a distância entre dois planos paralelos usando a fórmula, pois é só aplicar a fórmula e pronto, mas depende do problema. Além disso, achamos melhor explicar as duas formas de calcular a distância para que você possa escolher a que preferir.

Exemplo de cálculo da distância entre dois planos paralelos

Como exemplo, calcularemos a distância entre os dois planos a seguir:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

Devemos primeiro verificar se estamos lidando com dois planos paralelos. Assim, todos os coeficientes das equações planas são proporcionais, exceto os termos independentes, portanto são efetivamente dois planos paralelos.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

Neste caso, os termos A, B e C das equações dos dois planos não coincidem, mas podemos conseguir isso dividindo toda a equação do segundo plano por dois:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

Assim, as equações dos dois planos já possuem os mesmos coeficientes A, B e C. Portanto, podemos facilmente calcular a distância entre os dois planos com a fórmula da distância entre dois planos paralelos:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Substituímos os valores e resolvemos as operações:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

Para que a distância entre um plano e outro plano seja igual à unidade.

Resolvendo problemas de distância de um ponto a um plano

Exercício 1

Calcule a distância entre o ponto P e o plano cuja equação cartesiana (ou geral) é:

$P(2,0,-1) \qquad \qquad \pi: \ x-3y+2z-4=0$

veja solução

Para calcular a distância do ponto ao plano, você deve usar a fórmula correspondente:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Substituímos o valor de cada parâmetro na fórmula:

$d(P,\pi) = \cfrac{\lvert 1\cdot 2+(-3)\cdot 0+2\cdot (-1)-4\rvert}{\sqrt{1^2+(-3)^2+2^2}}$

E, por fim, fazemos as operações:

$d(P,\pi) = \cfrac{\lvert 2+0-2-4\rvert}{\sqrt{1+9+4}}$

$d(P,\pi) = \cfrac{\lvert -4\rvert}{\sqrt{14}}$

$\bm{d(P,\pi) = }\cfrac{\bm{4}}{\bm{\sqrt{14}}}$

Exercício 2

Encontre a distância entre o ponto P e o plano π:

$P(-1,4,3) \qquad \qquad \pi: \ y=5x-2z$

veja solução

Antes de usar a fórmula para a distância de um ponto a um plano, devemos primeiro expressar o plano na forma de uma equação implícita (ou geral):

$\pi: \ -5x+y+2z=0$

E agora podemos usar a fórmula para determinar a distância do ponto ao plano:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Substituímos o valor de cada termo na fórmula:

$d(P,\pi) = \cfrac{\lvert -5\cdot (-1)+1\cdot 4+2\cdot 3+0\rvert}{\sqrt{(-5)^2+1^2+2^2}}$

E, por fim, realizamos as operações:

$d(P,\pi) = \cfrac{\lvert 5+4+6\rvert}{\sqrt{25+1+4}}$

$\bm{d(P,\pi) = }\cfrac{\bm{15}}{\bm{\sqrt{30}}}$

Exercício 3

Use a fórmula da distância entre um ponto e um plano para determinar se o ponto P está no plano π.

$P(0,-3,5) \qquad \qquad \pi: \ 4x+6y+2z+8=0$

veja solução

Para verificar se o ponto pertence ao plano, podemos calcular a distância entre os dois: se a distância for zero isso implica que o ponto pertence ao plano, por outro lado se a distância for diferente de 0 isso significa que o ponto está fora do plano. plano.

Portanto, determinamos a distância entre o ponto e o plano a partir da fórmula:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

$d(P,\pi) = \cfrac{\lvert 4\cdot 0+6\cdot (-3)+2\cdot 5+8\rvert}{\sqrt{4^2+6^2+2^2}}$

$d(P,\pi) = \cfrac{\lvert -18+10+8\rvert}{\sqrt{16+36+4}}$

$d(P,\pi) = \cfrac{0}{\sqrt{56}}$

$\bm{d(P,\pi) = 0}$

A distância entre o ponto e o plano é equivalente a zero, então efetivamente o ponto pertence ao plano.

Exercício 4

Encontre a distância entre os dois planos a seguir:

$\pi_1 : \ 2x-y+5z-3=0 \qquad \qquad \pi_2 : \ 2x-y+5z-7=0$

veja solução

Devemos primeiro verificar se estamos lidando com dois planos paralelos. Todos os coeficientes das equações dos dois planos são proporcionais, com exceção dos termos independentes, portanto estes são de fato dois planos paralelos.

$\cfrac{2}{2}=\cfrac{-1}{-1}=\cfrac{5}{5} \neq \cfrac{-3}{-7} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

Neste caso calcularemos a distância entre os dois planos com a fórmula, pois seus coeficientes A, B e C são iguais:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Assim, substituímos os valores na fórmula e realizamos as operações:

$d(P,\pi) = \cfrac{\lvert -7-3\rvert}{\sqrt{2^2+(-1)^2+5^2}}= \cfrac{\lvert -10\rvert}{\sqrt{30}} = \cfrac{\bm{10}}{\bm{\sqrt{30}}}$

Exercício 5

Encontre a distância entre os seguintes dois planos paralelos:

$\pi_1 : \ \begin{cases} x=3+4\lambda-2 \mu \\[1.7ex]y=-2+\lambda+6 \mu \\[1.7ex]z=5-\lambda+3 \mu \end{cases}\qquad \qquad \pi_2 : \ 3x+2y-2z-9=0$

veja solução

O plano do primeiro plano é definido na forma de equações paramétricas, portanto, para aplicar a fórmula da distância entre dois planos paralelos temos que primeiro convertê-la na forma de uma equação geral e são necessários muitos cálculos e muito tempo. Portanto, é mais rápido pegarmos um ponto nesse plano e calcularmos a distância desse ponto ao outro plano.

Assim, as coordenadas de um ponto por onde passa o plano π ₁ correspondem aos termos independentes de cada equação paramétrica:

$P(3,-2,5)$