Nesta seção veremos como discutir e resolver um sistema de equações pelo método de Gauss-Jordan . Ou seja, determine se é um sistema compatível determinado (DCS), um sistema compatível indeterminado (ICS) ou um sistema incompatível. Além disso, você encontrará exemplos e exercícios resolvidos para que possa praticar e assimilar perfeitamente os conceitos.
Para entender o que vamos explicar a seguir, é importante que você já saiba como resolver um sistema pelo método Gauss , por isso recomendamos que você dê uma olhada antes de continuar.
Sistemas compatíveis determinados pelo método Gauss
Contanto que a última linha da matriz gaussiana seja
![]()
, ser
![]()
E
![]()
quaisquer dois números, este é um SCD (System Compatível Determinado). Portanto, o sistema possui uma solução única .
A grande maioria dos sistemas são SCD.
Exemplo:
Por exemplo, temos este sistema:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bab5d5823e45833aa691a3510a2a23eb_l3.png)
Cuja matriz expandida é:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}} \ \longrightarrow \ \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f8daea11edeedfd6b86bb251fe19032_l3.png)
Para resolver o sistema precisamos operar nas linhas da matriz e converter todos os elementos abaixo da diagonal principal em 0. Então da segunda linha subtraímos a primeira linha e da terceira linha subtraímos a primeira linha multiplicada por 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3 -2f_1} & \end{array} \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d68ac25745ddc71d1e7f55f68dd4ea7a_l3.png)
Uma vez que todos os números abaixo da diagonal principal sejam 0, voltamos para passar o sistema para a forma de equação:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 6y+2z=0\\[2ex] 1z=-3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4457f1b034e72c6945bfe609eff52b9a_l3.png)
Então esse sistema é SCD , pois a matriz é deslocada e a última linha é do tipo
![]()
. Portanto, resolvemos como sempre: eliminando as incógnitas das equações de baixo para cima.
![]()
![]()
![]()
Agora que sabemos z, substituímos seu valor na segunda equação para encontrar o valor de
![]()
:
![]()
![]()
![]()
![]()
![]()
E por fim, fazemos o mesmo com a primeira equação: substituímos os valores das outras incógnitas e resolvemos
![]()
:
![]()
![]()
![]()
![]()
![]()
![]()
A solução do sistema de equações é, portanto:
![]()
Sistemas incompatíveis pelo método de Gauss
Quando na matriz de Gauss temos uma linha com três 0s consecutivos e um número
![]()
, é um SI (Sistema Incompatível) e, portanto, o sistema não tem solução .
Exemplo:
Por exemplo, imagine que após operar com a matriz gaussiana de um sistema, ficamos com:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & 1 & -1 & 0 \\[2ex] 0 & 3 & 1 & -1 \\[2ex] 0 & 0 & 0 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-defe65fa616eff800314ebc6dc6f552b_l3.png)
Como a última linha é
![]()
, ou seja, três 0s seguidos de um número no final, é um SE (Sistema Incompatível) e, portanto, o sistema não tem solução .
Embora não seja necessário saber, a seguir você verá porque não tem solução.
Se pegarmos a última linha, teríamos esta equação:
![]()
Esta equação nunca será cumprida, porque qualquer que seja o valor que z assuma, multiplicá-lo por 0 nunca dará 2 (qualquer número multiplicado por 0 sempre dará 0). E como esta equação nunca será cumprida, o sistema não tem solução.
Sistemas compatíveis indeterminados pelo método gaussiano
Sempre que uma linha da matriz gaussiana é preenchida com 0
![]()
, é um SCI (Sistema Compatível Indeterminado) e, portanto, o sistema possui infinitas soluções .
Vejamos um exemplo de como resolver um ICS:
Exemplo:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-18a63dfebc1f23923714e475aad2e808_l3.png)
Como sempre, primeiro fazemos a matriz expandida do sistema :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\} \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f273040101827fdfea5c9a4858be5567_l3.png)
Agora queremos que todos os números abaixo da diagonal principal sejam 0. Então, à segunda linha adicionamos a primeira linha multiplicada por -2:
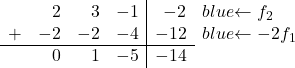
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c889a6f147c6b0430731aa778121af52_l3.png)
Para converter 3 em 0, na terceira linha adicionamos a primeira linha multiplicada por -3:
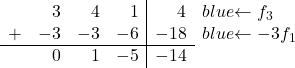
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5acccc51108267fef6d3320068743aa_l3.png)
Para converter o 1 da última linha em 0, na terceira linha adicionamos a segunda linha multiplicada por -1:

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a02e4819adfbe7b80d2952f87f113757_l3.png)
Como a última linha é toda 0 , podemos removê-la:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6aea469dceab08e6aa62571922eb2824_l3.png)
E como tivemos uma linha inteira preenchida com 0s, este é um SCI.
Terminamos, portanto, com o seguinte sistema:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y+2z=6 \\[2ex] y-5z=-14 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-598c031f4cba5a865952a57ed46f0f95_l3.png)
Quando o sistema é um SCI, é necessário retirar o valor do parâmetro de um valor desconhecido
![]()
. E precisamos resolver o sistema com base neste parâmetro
![]()
.
Portanto, atribuímos o valor de
![]()
para z :
![]()
Embora também pudéssemos ter escolhido qualquer outra incógnita para assumir o valor de
![]()
.
Agora isolamos y da segunda equação e deixamos que seja uma função de
![]()
:
![]()
![]()
![]()
E finalmente excluímos x da primeira equação e também o deixamos como uma função de
![]()
:
![]()
![]()
![]()
![]()
As soluções do sistema são, portanto:
![]()
Como você pode ver, quando o sistema é SCI deixamos as soluções dependendo do parâmetro
![]()
. E lembre-se que tem infinitas soluções, pois dependendo do valor que leva
![]()
, a solução será uma ou outra.
Antes de passar aos exercícios resolvidos, você deve saber que embora neste artigo utilizemos o método de Gauss, outra forma de discutir e resolver sistemas de equações lineares é o teorema de Rouche . Na verdade, provavelmente é mais usado.
Exercícios resolvidos para discussão de sistemas de equações pelo método Gauss-Jordan
Exercício 1
Determine que tipo de sistema está envolvido e resolva o seguinte sistema de equações usando o método de Gauss:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be4ba1bd1ce7452e66c5189d995d948c_l3.png)
A primeira coisa que precisamos fazer é a matriz estendida do sistema:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex] 3 & 3 & 6 & 9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b600f3fc0d79a06eb972dbacb673a780_l3.png)
Agora precisamos fazer com que todos os números abaixo do array principal sejam 0.
Portanto, realizamos operações de linha para cancelar os dois últimos termos da primeira coluna:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex]3 & 3 & 6 & 9 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_1} \\[2ex] \xrightarrow{f_3 - 3f_1}& \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & 1 & -4 \\[2ex] 0 & 0 & 0 & -9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1d832d5bb115666614ae96822c360eb_l3.png)
Obtivemos uma linha da matriz composta por três 0s seguidos de um número. É portanto um SI (Sistema Incompatível) e o sistema não tem solução.
Exercício 2
Determine que tipo de sistema é e encontre a solução para o seguinte sistema de equações usando o método de Gauss:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f5aba495f2c6a301e923ee3c6238012_l3.png)
A primeira coisa que precisamos fazer é a matriz estendida do sistema:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8bb5e5ab85946bddad72067fe17d937_l3.png)
Agora precisamos fazer com que todos os números abaixo do array principal sejam 0.
Portanto, realizamos operações de linha para cancelar os dois últimos termos da primeira coluna:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 2f_1} \\[2ex] \xrightarrow{f_3 + f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e48becaaa6683719ac57eb7d118943_l3.png)
Agora vamos tentar remover o último elemento da segunda coluna:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-16a1afc0eb224ee5f05c9e313586854d_l3.png)
Mas obtemos uma linha inteira de 0s. Portanto, este é um SCI e o sistema tem infinitas soluções.
Mas como é um ICS, podemos resolver o sistema com base em
![]()
. Portanto, excluímos a linha 0:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c838c5f1b229d4c8a43ac9ddd8e3629_l3.png)
Expressamos agora a matriz na forma de um sistema de equações com incógnitas:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-2y+3z=1 \\[2ex] 1y+5z=7 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3fd941d33fec646d16b8181430c9986_l3.png)
Damos o valor de
![]()
Para
![]()
![]()
Substituímos o valor de
![]()
na segunda equação para encontrar o valor de
![]()
![]()
![]()
![]()
E fazemos o mesmo com a primeira equação: substituímos os valores das outras incógnitas e apagamos
![]()
![]()
![]()
![]()
![]()
A solução do sistema de equações é, portanto:
![]()
Exercício 3
Descubra que tipo de sistema é e resolva o seguinte sistema de equações pelo método de Gauss:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b04370b42854e53c650ca0eae14aadb5_l3.png)
A primeira coisa que precisamos fazer é a matriz estendida do sistema:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff2c7644e19fdf405f3c5c42ffc0ee98_l3.png)
Para aplicar o método de Gauss, é mais simples se o primeiro número da primeira linha for 1. Portanto, alteraremos a ordem das linhas 1 e 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 \rightarrow f_2} \\[2ex] \xrightarrow{f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-471d89605d4bf6ddef1896a8fbe4c5ea_l3.png)
Agora precisamos fazer com que todos os números abaixo do array principal sejam 0.
Portanto, realizamos operações de linha para cancelar os dois últimos termos da primeira coluna:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 4f_1} \\[2ex] \xrightarrow{f_3 -f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f4d5cbc50b87927077018175c4678e90_l3.png)
Agora convertemos o último elemento da segunda coluna em zero:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{8f_3 + f_2} \end{array} \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9013720883fd719e2bd0779bfbaa7a9f_l3.png)
Esse sistema é o SCD , pois conseguimos deslocar a matriz e a última linha é do tipo
![]()
. Portanto, terá uma solução única.
Quando todos os números abaixo da diagonal principal forem 0, podemos agora resolver o sistema de equações. Para fazer isso, expressamos a matriz novamente na forma de um sistema de equações com incógnitas:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+1z=2 \\[2ex] -16y-3z=-12 \\[2ex] 5z=20 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0f0433738d5d0a22bdd3b04dbd44fd1e_l3.png)
E resolvemos as incógnitas das equações de baixo para cima. Primeiro resolvemos a última equação:
![]()
![]()
Agora substituímos o valor de z na segunda equação para encontrar o valor de y:
![]()
![]()
![]()
![]()
![]()
E fazemos o mesmo com a primeira equação: substituímos os valores das outras incógnitas e resolvemos para x:
![]()
![]()
![]()
![]()
A solução do sistema de equações é, portanto:
![]()
Exercício 4
Determine que tipo de sistema é e resolva o seguinte sistema de equações pelo método de Gauss:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e8a133547b4719d7833a792550fd322_l3.png)
A primeira coisa que precisamos fazer é a matriz estendida do sistema:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc41f78456a922a0fbff419d336b0b46_l3.png)
Agora precisamos fazer com que todos os números abaixo do array principal sejam 0.
Portanto, realizamos operações de linha para cancelar os dois últimos termos da primeira coluna:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 3f_1} \\[2ex] \xrightarrow{f_3 + 2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff92912f653c6aca7ceb7c990c9635a3_l3.png)
Agora vamos tentar remover o último elemento da segunda coluna:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c6904a64a721f3a92bef8c6b7d713cf_l3.png)
Mas obtemos uma linha inteira de 0s. Portanto, este é um SCI e o sistema tem infinitas soluções.
Mas como é um ICS, podemos resolver o sistema com base em
![]()
. Portanto, excluímos a linha 0:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6d856e2c1246f3629d68a7bcd3cd759a_l3.png)
Expressamos agora a matriz na forma de um sistema de equações com incógnitas:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-1y+4z=2 \\[2ex] -6y+15z=13 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4cf1265bfc12f94580de183230c8b7c_l3.png)
Damos o valor de
![]()
Para
![]()
![]()
Substituímos o valor de
![]()
na segunda equação para encontrar o valor de
![]()
![]()
![]()
![]()
![]()
E fazemos o mesmo com a primeira equação: substituímos os valores das outras incógnitas e apagamos
![]()
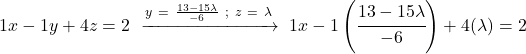
![]()
![]()
Temos uma soma com frações. Portanto, reduzimos todos os termos a um denominador comum:
![]()
![]()
Como agora todos têm o mesmo denominador, podemos agrupá-los em uma única fração:
![]()
E finalmente operamos no numerador:
![]()
![]()
A solução do sistema de equações é, portanto:
![]()