Como calcular o determinante de uma matriz 2×2

Nesta página você aprenderá o que é o determinante de uma matriz 2×2. Além disso, você encontrará exemplos resolvidos passo a passo e exercícios sobre como resolver determinantes de ordem 2, para que possa praticar e entender perfeitamente.

O que é um determinante 2×2?

Um determinante de ordem 2 é uma matriz de dimensão 2 × 2 representada por uma barra vertical em cada lado da matriz. Por exemplo, se tivermos a seguinte matriz:

\displaystyle A = \begin{pmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}

O determinante da matriz A é representado da seguinte forma:

\displaystyle \lvert A \rvert = \begin{vmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{vmatrix}

Como você viu, escrever o determinante de uma matriz quadrada 2×2 é fácil. Agora vamos ver como é calculado:

Como resolver um determinante de ordem 2?

Para calcular o determinante de uma matriz 2×2, precisamos multiplicar os elementos da diagonal principal e subtrair o produto da diagonal secundária.

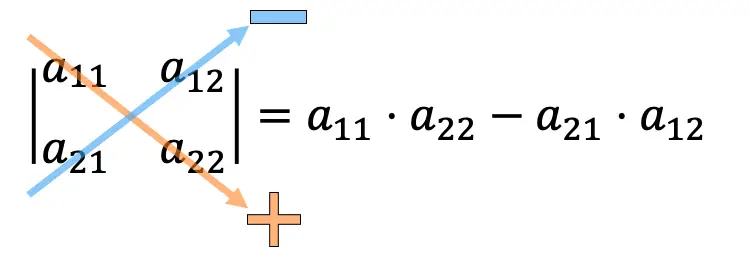
exemplo de cálculo do determinante de uma matriz 2x2

Exemplos de cálculo de determinantes 2×2:

\displaystyle\begin{vmatrix} 3 & 4 \\[1.1ex] 2 & 1 \end{vmatrix} = 3 \cdot 1 - 2 \cdot 4 = 3 - 8 = \bm{-5}

\displaystyle\begin{vmatrix} 2 & -3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot (-3) =10-(-3) = 10+3= \bm{13}

Problemas resolvidos de determinantes de matrizes 2 × 2

Exercício 1

Calcule o seguinte determinante 2×2:

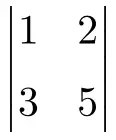
exercício resolvido passo a passo do determinante 2x2

Para fazer um determinante 2×2, você deve multiplicar os elementos da diagonal principal e subtrair o produto da diagonal secundária:

\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 3 & 5 \end{vmatrix} = 1 \cdot 5 - 3 \cdot 2 = 5 - 6 = \bm{-1}

Exercício 2

Resolva o seguinte determinante de dimensão 2×2:

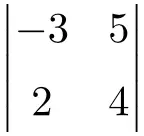
exercícios resolvidos passo a passo de determinantes 2x2

Para encontrar a solução de um determinante de ordem 2, deve-se multiplicar os elementos da diagonal principal e subtrair o produto da diagonal secundária:

\displaystyle \begin{vmatrix} -3 & 5 \\[1.1ex] 2 & 4 \end{vmatrix} = -3 \cdot 4 - 2 \cdot 5 = -12 - 10 = \bm{-22}

Exercício 3

Encontre a solução para o seguinte determinante de ordem 2:

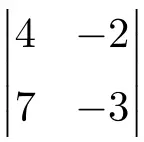
exercício resolvido passo a passo de um determinante de uma matriz 2x2

Para encontrar a solução para um determinante de dimensão 2, deve-se multiplicar os elementos da diagonal principal e subtrair o produto da diagonal secundária:

\displaystyle \begin{vmatrix} 4 & -2 \\[1.1ex] 7 & -3\end{vmatrix} = 4 \cdot (-3) - 7 \cdot (-2) = -12 - (-14) =-12+14= \bm{2}

Exercício 4

Calcule o seguinte determinante 2×2:

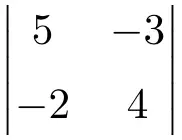
como resolver o determinante de uma matriz 2x2, exercício resolvido passo a passo

Para calcular os determinantes de matrizes 2×2, precisamos multiplicar os elementos da diagonal principal e subtrair o produto da diagonal secundária:

\displaystyle \begin{vmatrix} 5 & -3 \\[1.1ex] -2 & 4\end{vmatrix} = 5 \cdot 4 - (-2) \cdot (-3) = 20 - (+6) = \bm{14}

Exercício 5

Determine o resultado do seguinte determinante 2×2:

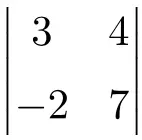
Exercício resolvido sobre a resolução passo a passo do determinante de uma matriz de ordem 2

Para encontrar a solução para um determinante 2×2, precisamos multiplicar os elementos da diagonal principal e subtrair o produto da diagonal secundária:

\displaystyle \begin{vmatrix} 3 & 4 \\[1.1ex] -2 & 7\end{vmatrix} = 3 \cdot 7 - (-2) \cdot 4 = 21 - (-8)=21+8 = \bm{29}

Brilhante! Agora você sabe criar determinantes de dimensão 2×2! Agora com certeza você já consegue entender como o determinante 3×3 é calculado e também como é resolvido o determinante de uma matriz 4×4 .

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima