Derivada do cosseno do arco hiperbólico

Nesta página você verá qual é a derivada do arco cosseno hiperbólico (fórmula). Você também encontrará exercícios resolvidos passo a passo para derivadas do arco cosseno hiperbólico de uma função. E, por fim, você encontrará a demonstração da fórmula da derivada desse tipo de função trigonométrica.

Fórmula para a derivada do arco cosseno hiperbólico

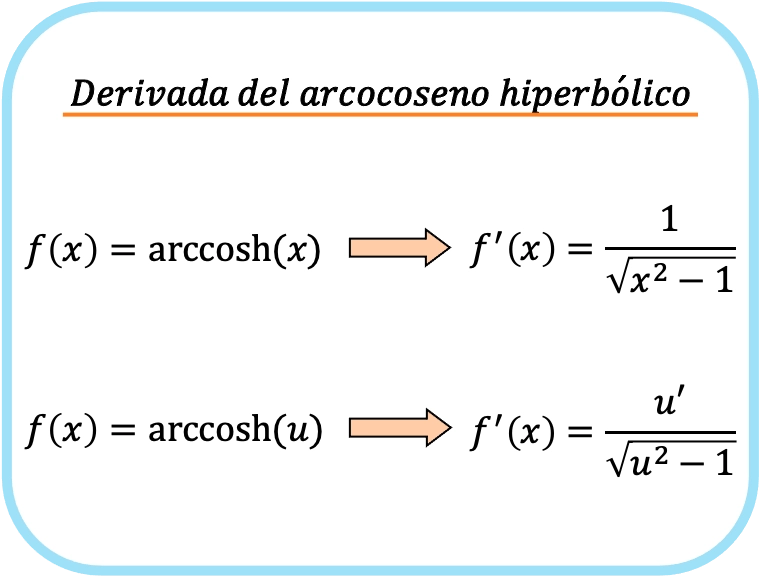
A derivada do arco cosseno hiperbólico de x é um sobre a raiz quadrada de x ao quadrado menos 1.

$f(x)=\text{arccosh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{x^2-1}}$

Portanto, a derivada do arco cosseno hiperbólico de uma função é igual ao quociente da derivada dessa função dividido pela raiz quadrada dessa função ao quadrado menos um.

$f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}$

A segunda fórmula inclui a regra da cadeia e, portanto, pode ser usada para derivar qualquer arco cosseno hiperbólico. Na verdade, se substituirmos x por u, obteremos a primeira fórmula. Em vez disso, a primeira fórmula só funciona para a derivada arcocoseno hiperbólica de x.

O arco cosseno hiperbólico é a função inversa do cosseno hiperbólico e, portanto, as duas funções estão relacionadas. Você pode ver a fórmula da derivada desta função trigonométrica clicando aqui:

➤ Veja: fórmula da derivada do cosseno hiperbólico

Exemplos da derivada hiperbólica do arco seno

Exemplo 1

$f(x)=\text{arccosh}(5x)$

Para encontrar a derivada do arco cosseno hiperbólico, precisamos usar sua fórmula correspondente, que é:

$f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}$

Portanto, no numerador da fração precisamos colocar a derivada de 5x, que é 5. E no denominador só precisamos colocar a raiz quadrada da função argumento ao quadrado menos 1:

$f(x)=\text{arccosh}(5x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{5}{\sqrt{(5x)^2-1}}=\cfrac{5}{\sqrt{25x^2-1}}$

Exemplo 2

$f(x)=\text{arccosh}(x^4-5x^2)$

A função a ser derivada deste exercício é um arco cosseno hiperbólico, então usamos a seguinte fórmula para derivá-la:

$f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}$

Assim, no numerador escrevemos a derivada do argumento da função e no denominador a raiz quadrada da função do argumento elevado a 2 menos 1:

$f(x)=\text{arccosh}(x^4-5x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{4x^3-10x}{\sqrt{\left(x^4-5x^2\right)^2-1}}$

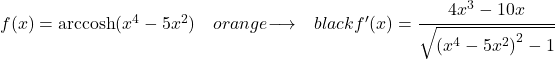
Prova da derivada do arco cosseno hiperbólico

Por fim, demonstraremos a fórmula da derivada do arco cosseno hiperbólico.

$y=\text{arccosh}(x)$

Primeiro, transformamos o cosseno do arco hiperbólico em um cosseno hiperbólico:

$x=\text{cosh}(y)$

Deduzimos de ambos os lados da igualdade:

$1=\text{senh}(y)\cdot y'$

Nós limpamos você:

$y'=\cfrac{1}{\text{senh}(y)}$

Agora usamos a identidade trigonométrica que relaciona o seno hiperbólico e o cosseno hiperbólico para modificar o denominador:

$\text{cosh}^2(y)-\text{senh}^2(y)=1 \ \longrightarrow \ \text{senh}(y)=\sqrt{\text{cosh}^2(y)-1}$

$y'=\cfrac{1}{\sqrt{\text{cosh}^2(y)-1}}$

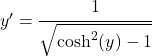
Porém, primeiro, deduzimos que x é equivalente ao cosseno hiperbólico de y, então a equação permanece:

$y'=\cfrac{1}{\sqrt{x^2-1}}$

Derivada do arco cosseno hiperbólico

Fórmula para a derivada do arco cosseno hiperbólico

Exemplos da derivada hiperbólica do arco seno

Exemplo 1

Exemplo 2

Prova da derivada do arco cosseno hiperbólico

itens similares

Deixe um comentário Cancelar resposta