Derivada do seno hiperbólico

Aqui você descobrirá como derivar o seno hiperbólico (fórmula). Além disso, você verá vários exemplos resolvidos da derivada do seno hiperbólico. E por fim, provamos a fórmula da derivada deste tipo de função trigonométrica.

Fórmula derivada do seno hiperbólico

A derivada do seno hiperbólico de x é o cosseno hiperbólico de x.

$f(x)=\text{senh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x)$

Portanto, a derivada do seno hiperbólico de uma função é igual ao produto do cosseno hiperbólico da função e a derivada dessa função.

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

Na verdade, as duas fórmulas acima são iguais, a única diferença é que na segunda fórmula aplicamos a regra da cadeia. E como a derivada de x é 1, isso não altera a função.

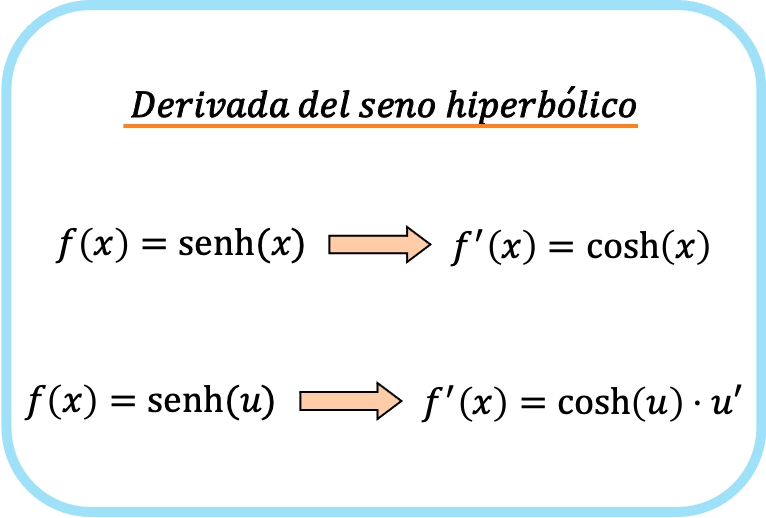
Como você pode ver, a fórmula da derivada senoidal hiperbólica é muito semelhante à fórmula da derivada senoidal .

Exemplos da derivada seno hiperbólica

Uma vez que já vimos o que é a fórmula da derivada do seno hiperbólico, passamos agora a resolver vários exemplos da derivada do seno hiperbólico. Então, certamente você não tem dúvidas sobre como isso é feito.

Exemplo 1: Derivada do seno hiperbólico de 2x

$f(x)=\text{senh}(2x)$

Neste caso, no argumento do seno hiperbólico, temos uma função diferente de x, portanto, devemos utilizar a fórmula da derivada do seno hiperbólico com a regra da cadeia para encontrar a derivada:

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

A derivada de 2x é 2, então a derivada do seno hiperbólico de 2x será o cosseno hiperbólico de 2x vezes 2.

$f(x)=\text{senh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(2x)\cdot 2=2\text{cosh}(2x)$

Exemplo 2: Derivada do seno hiperbólico de x ao quadrado

$f(x)=\text{senh}(x^2)$

A fórmula para a derivada da função seno hiperbólica é:

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

Por outro lado, a derivada da função quadrática x ² é 2x. A derivada de toda a função é, portanto:

$f(x)=\text{senh}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x^2)\cdot 2x$

Prova da fórmula da derivada do seno hiperbólico

Por fim, demonstraremos a fórmula da derivada do seno hiperbólico. Para isso, partiremos da definição matemática do seno hiperbólico:

$\text{senh}(x)=\cfrac{e^x-e^{-x}}{2}$

Deduzimos agora os dois lados da igualdade:

$\displaystyle\bigl(\text{senh}(x)\bigr)'=\left(\frac{e^x-e^{-x}}{2}\right)'$

Para derivar o lado direito da equação, usaremos a fórmula da derivada da divisão:

$\displaystyle\text{senh}'(x)=\frac{(e^x+e^{-x})\cdot 2}{2^2}=\frac{e^x+e^{-x}}{2}$

➤ Veja: derivada da função exponencial com base e

E chegámos precisamente à expressão que define o cosseno hiperbólico. Para que a derivada do seno hiperbólico seja provada:

$\displaystyle\text{senh}'(x)=\text{cosh}(x)$

Fórmula derivada do seno hiperbólico

Exemplos da derivada seno hiperbólica

Exemplo 1: Derivada do seno hiperbólico de 2x

Exemplo 2: Derivada do seno hiperbólico de x ao quadrado

Prova da fórmula da derivada do seno hiperbólico

Deixe um comentário Cancelar resposta