Derivada do arco tangente hiperbólico

Aqui você descobrirá como derivar o arco tangente hiperbólico de uma função. Você também poderá ver exemplos resolvidos deste tipo de derivadas trigonométricas e, por fim, mostraremos a fórmula da derivada do arco tangente hiperbólico.

Fórmula para a derivada do arco tangente hiperbólico

A derivada do arco tangente hiperbólico de x é um sobre um menos x ao quadrado.

f(x)=\text{arctanh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{1-x^2}

Portanto, a derivada do arco tangente hiperbólico de uma função é igual ao quociente da derivada dessa função dividido por um menos a referida função ao quadrado.

f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

Na verdade, ambas as fórmulas são iguais, mas na segunda aplica-se a regra da cadeia. Por exemplo, substituir x por u nos dá exatamente a primeira fórmula, já que a derivada de x é 1.

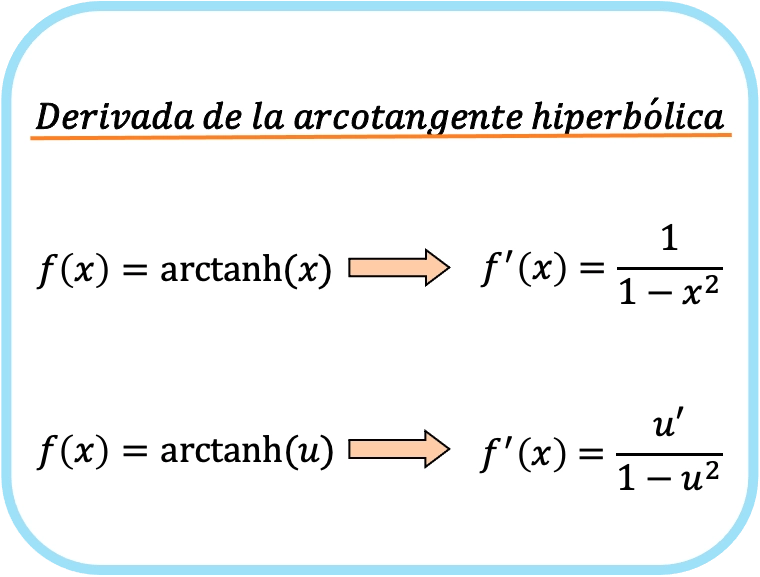
derivada do arco tangente hiperbólico

Assim como o arco tangente é a função inversa da tangente, o arco tangente hiperbólico é o inverso da tangente hiperbólica. Mesmo assim suas derivadas são bem diferentes, você pode conferir a derivada dessa função trigonométrica aqui:

➤ Veja: fórmula da derivada da tangente hiperbólica

Exemplos de derivada de arco tangente hiperbólico

Exemplo 1

f(x)=\text{arctanh}(2x)

Logicamente, devemos aplicar a regra da derivada do arco tangente hiperbólico:

f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

A derivada de 2x é 2, então coloque dois no numerador da fração e um menos 2x ao quadrado no denominador:

f(x)=\text{arctanh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{1-(2x)^2}}=\cfrac{2}{1- 4x^2}

Exemplo 2

f(x)=\text{arctanh}(e^{3x})

Para resolver a derivada desta função, precisamos de utilizar a fórmula da derivada do arco tangente hiperbólico.

f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

Além disso, a função do argumento arco tangente hiperbólico é uma função composta, portanto também precisaremos aplicar a regra da cadeia:

f(x)=\text{arctanh}(e^{3x}) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3\cdot e^{3x}}{1-\left(e^{3x}\right)^2}=\cfrac{3e^{3x}}{1-3^{6x}}

Prova da derivada do arco tangente hiperbólico

Nesta seção final, demonstraremos a fórmula da derivada do arco tangente hiperbólico.

y=\text{arctanh}(x)

Como a tangente hiperbólica é a tangente hiperbólica inversa, podemos expressar a igualdade anterior de outra forma:

x=\text{tanh}(y)

Agora diferenciamos ambos os lados da equação:

1=\cfrac{1}{\text{cosh}^2(y)}\cdot y'

Nós limpamos você:

y'=\text{cosh}^2(y)

Por outro lado, sabemos que a diferença dos quadrados do cosseno hiperbólico e do seno hiperbólico dá 1. Podemos portanto transformar a expressão anterior numa fração:

\text{cosh}^2(y)-\text{senh}^2(y)=1

y'=\cfrac{\text{cosh}^2(y)}{1}=\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)-\text{senh}^2(y)}

Dividimos todos os termos da fração pelo quadrado do cosseno hiperbólico:

y'=\cfrac{\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)}}{\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)}-\cfrac{\text{senh}^2(y)}{\text{cosh}^2(y)}}

y'=\cfrac{1}{1-\cfrac{\text{senh}^2(y)}{\text{cosh}^2(y)}}

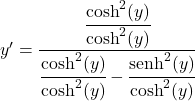
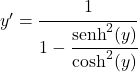
O quociente do seno hiperbólico entre o cosseno hiperbólico é igual à tangente hiperbólica, portanto:

\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}

y'=\cfrac{1}{1-\text{tanh}^2(y)}

Mas, como vimos no início da prova, a tangente hiperbólica é equivalente à variável x, podemos portanto substituir a expressão obtendo assim a fórmula da derivada da tangente do arco hiperbólico:

y'=\cfrac{1}{1-x^2}

itens similares

Deixe um comentário

O seu endereço de e-mail não será publicado. Campos obrigatórios são marcados com *

Rolar para cima