Neste artigo, você aprenderá como derivar o arco tangente de uma função. Além disso, você poderá ver exemplos desse tipo de derivada e até praticar com exercícios resolvidos sobre a derivada do arco tangente. Por fim, mostramos também a prova da fórmula da derivada do arco tangente.
Qual é a derivada do arco tangente?
A derivada do arco tangente de x é um sobre um mais x ao quadrado.
![]()
Portanto, a derivada do arco tangente de uma função é igual ao quociente da derivada dessa função dividido por um mais a referida função ao quadrado.
![]()
Neste caso, a função foi representada por au, então esta seria a fórmula da derivada do arco tangente da função u.
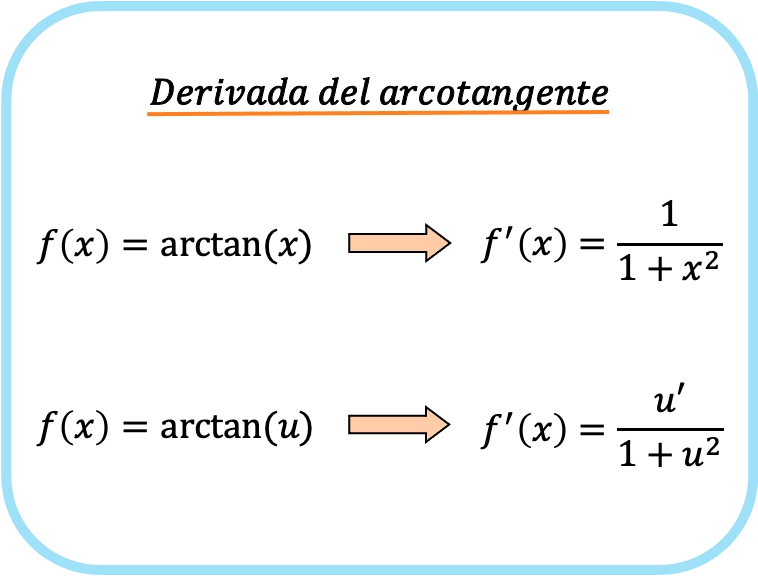
Como você pode ver, a fórmula da derivada da tangente inversa é muito semelhante às fórmulas das derivadas do arco seno e do arco cosseno.
Exemplos de derivada do arco tangente
Uma vez conhecida a fórmula da derivada do arco tangente, explicaremos a derivação de vários exemplos deste tipo de derivadas trigonométricas. Dessa forma, será mais fácil entender como o arco tangente de uma função é derivado.
Exemplo 1: Derivada do arco tangente de 2x
![]()
Aplicamos a fórmula para resolver a derivada:
![]()
A derivada de 2x é 2, então a derivada arco tangente de 2x é 2 sobre um mais 2x ao quadrado:
![]()
Exemplo 2: Derivada do arco tangente de x ao quadrado
![]()
Para encontrar o resultado da derivada deste exemplo, precisamos usar a fórmula da derivada do arco tangente, que é:
![]()
Assim, a derivada da função x 2 é 2x, então a derivada do arco tangente de x elevado à potência de 2 é:
![]()
Exemplo 3: Derivada do arco tangente do seno de x
![]()
Logicamente, para calcular a derivada deve-se aplicar a fórmula correspondente:
![]()
Neste caso temos uma função composta, portanto devemos aplicar a regra da cadeia para calcular a derivada do arco tangente:
![]()
Exercícios resolvidos sobre a derivada do arco tangente
Derive as seguintes funções arco tangente:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
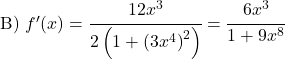
![]()
![]()
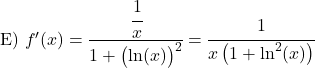
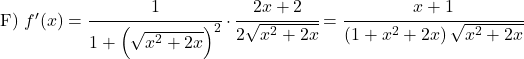
Demonstração da fórmula da derivada do arco tangente
A seguir, provaremos a fórmula da derivada do arco tangente.
![]()
Primeiro convertemos o arco tangente em tangente aproveitando o fato de que o arco tangente é a função inversa da tangente:
![]()
Diferenciamos os dois lados da equação:
![]()
Nós apagamos e’:
![]()
Por outro lado, graças à identidade trigonométrica fundamental sabemos que a soma dos quadrados do seno e do cosseno é igual a 1. Podemos portanto transformar a expressão anterior numa fração:
![]()
![]()
Dividimos todos os termos pelo quadrado do cosseno:
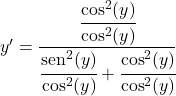
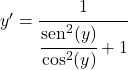
O seno dividido pelo cosseno é igual à tangente, então:
![]()
![]()
Como vimos acima, a tangente equivale à variável x, podemos portanto substituir a expressão para chegar à fórmula da derivada do arco tangente:
![]()