Aqui você descobrirá como calcular a derivada do arco secante hiperbólico de uma função. Além disso, você poderá ver exemplos resolvidos da derivada do arco secante hiperbólico.
Fórmula derivada do arco secante hiperbólico
A derivada do arco secante hiperbólico de x é igual a menos 1 dividido pelo produto de x vezes a raiz de um menos x ao quadrado.
![]()
Portanto, a derivada do arco secante hiperbólico de uma função é menos a derivada dessa função dividida pelo produto da função vezes a raiz de um menos a função quadrada.
![]()
Resumindo, a fórmula para a derivada da função arcosecante hiperbólica é:
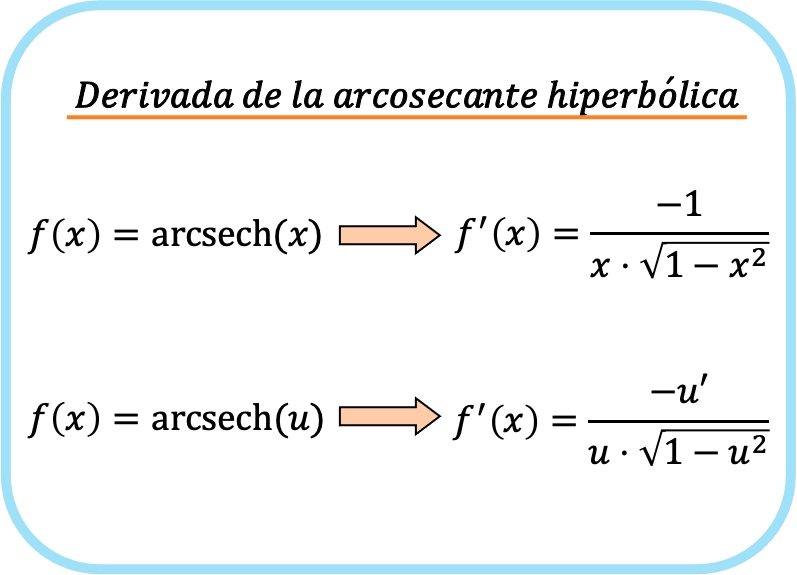
Na verdade, ambas as expressões correspondem à mesma fórmula, mas a regra da cadeia é aplicada à segunda fórmula. Na verdade, se você substituir u pela função identidade x, obterá a primeira fórmula, pois a derivada de x é 1.
Exemplos de derivada do arco secante hiperbólico
Depois de ver qual é a fórmula da derivada do arco secante hiperbólico, resolveremos passo a passo dois exercícios deste tipo de derivadas trigonométricas inversas. Assim, você pode ver exatamente como derivar o arco secante hiperbólico de uma função.
Exemplo 1
Neste exemplo, determinaremos qual é a derivada do arco secante hiperbólico 2x.
![]()
No argumento do arco secante hiperbólico, temos uma função diferente de x, então precisamos usar a fórmula da regra da cadeia para derivá-la:
![]()
A função 2x é linear, então sua derivada é 2. Portanto, para encontrar a derivada, simplesmente substituímos 2x por u e 2 por u’ na fórmula:
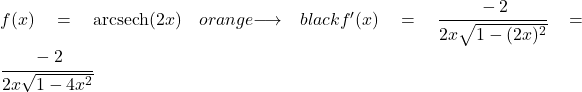
Exemplo 2
Neste segundo exercício, derivaremos o arco secante hiperbólico de uma função polinomial:
![]()
A função deste exercício é composta, pois o arco secante hiperbólico tem outra função em seu argumento. Portanto, precisamos usar a fórmula da derivada do arco secante hiperbólico com a regra da cadeia para fazer sua derivação:
![]()
Portanto, no numerador da fração colocamos a derivada da função polinomial do argumento, e no denominador trocamos o u pela função polinomial:
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\text{arcsech}(x^3-4x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(3x^2-4)}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\\[1.5ex] &=\cfrac{-3x^2+4}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f6389de5c7761fb5d35a9861156eec1_l3.png)