Aqui explicamos como derivar uma potência (ou função potencial), você encontrará a fórmula da derivada de uma potência, vários exemplos e poderá até praticar com exercícios resolvidos passo a passo.
Fórmula para a derivada de uma potência
A derivada de uma potência, ou função potencial, é o produto do expoente da potência vezes a base elevada ao expoente menos 1 vezes a derivada da base.
![]()
Portanto, se a base for a função identidade , para obter a potência, basta multiplicar a função pelo expoente e subtrair uma unidade do expoente:
![]()
Na verdade, a derivada da função identidade é igual a 1.
Em resumo, para derivar uma função potencial, existem duas fórmulas: a primeira que sempre pode ser usada e a segunda que só pode ser aplicada quando a base for um x.
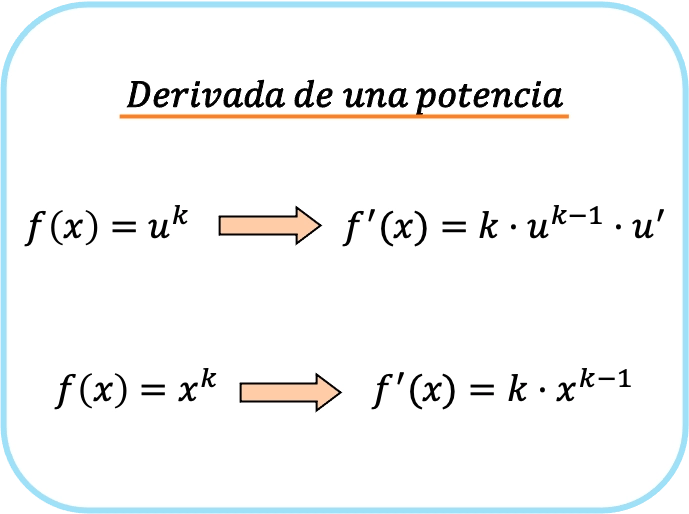
Podemos facilmente verificar que a primeira fórmula apresentada para a derivada de uma potência é semelhante à segunda, mas aplicando a regra da cadeia.
Observe que essas fórmulas só podem ser usadas quando a variável é a base da potência, se o x estiver no denominador você deve aplicar a regra para a derivada de uma função exponencial:
➤ Veja: derivada de uma função exponencial
Exemplos de derivados de potência
Depois de vermos a fórmula da derivada de uma função potencial, explicaremos vários exemplos deste tipo de derivada para que você entenda como as potências são derivadas.
Exemplo 1: Derivada de uma potência base x
![]()
Como explicamos na seção anterior, quando a base da potência é apenas x, a fórmula que devemos usar para derivar a função é:
![]()
A derivada da potência x elevada à potência de 4 é, portanto:
![]()
Exemplo 2: Derivada de uma potência com parênteses
![]()
Neste exemplo a base não é a função identidade, devemos portanto usar a fórmula geral para a derivada de uma potência:
![]()
A função entre parênteses é uma função linear, então sua derivada é 2. Portanto, a derivada de toda a função potencial é:
![]()
Exemplo 3: Derivada de uma potência negativa
![]()
Neste caso temos uma função potencial cujo expoente é negativo e cuja base é um logaritmo, portanto utilizaremos a seguinte fórmula para diferenciar a função:
![]()
Mesmo que o expoente da potência seja negativo, também deve ser subtraído dele. A derivada da função é, portanto:
![]()
Se tiver alguma dúvida sobre a solução, pode consultar aqui a fórmula da derivada de uma função logarítmica:
➤ Veja: derivada de uma função logarítmica
Exemplo 4: Derivada de uma potência com raiz
![]()
A função neste exemplo é uma potência dentro de uma expressão regular. No entanto, os radicais podem ser transformados em expressões potenciais, de modo que a função pode ser simplificada convertendo-a em uma função potencial com um expoente fracionário:
![]()
Aplicamos agora a fórmula para a derivada de uma potência de uma variável:
![]()
E a derivada é:
![]()
Você também pode diferenciar esses tipos de funções usando a regra da derivada raiz:
➤ Veja: derivado de uma raiz
Exercícios resolvidos sobre a derivada de uma potência
Calcule a derivada das seguintes potências:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
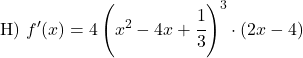
![]()