Neste artigo explicamos como derivar um quociente (ou divisão) de duas funções. Você encontrará exemplos de derivadas de quocientes de funções e, além disso, poderá praticar com exercícios passo a passo sobre derivadas de divisões.
Fórmula para a derivada de um quociente
A derivada de um coeficiente (ou divisão) das funções é idêntica à derivada da função numerador pela função denominador menos do que a função numerador pela derivada da função denominador dividida pelo quadrado da função de denominador alto.

Como você pode ver, quando aplicamos a regra da derivada de um quociente (ou de uma divisão), ainda temos uma fração após a diferenciação. Mas, além disso, no numerador temos duas multiplicações e uma subtração, e o denominador é elevado à potência de dois.
Exemplos de derivadas de quocientes
Acabamos de ver qual é a fórmula da derivada de um quociente de duas funções, a seguir resolveremos vários exemplos de derivadas deste tipo de operações. Lembre-se, se você não entende como um quociente funcional é derivado, pergunte-nos na seção de comentários.
Exemplo 1
Neste exemplo, derivaremos uma função potencial dividida por uma função trigonométrica:
![]()
A fórmula para a derivada de uma divisão de duas funções diferentes é a seguinte:
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc09ff88e92ee46b5c98d6fc81a5d5a6_l3.png)
Então primeiro precisamos calcular a derivada de cada função separadamente:
![]()
![]()
A derivada de toda a função é, portanto:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(6x+4)\cdot\text{sen}(2x)-(3x^2+4x)\cdot 2\text{cos}(2x)}{\text{sen}^2(2x)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-65ce4673f3ad5a4c09a9b2e7c611821d_l3.png)
Exemplo 2
Neste caso encontraremos a derivada de uma constante dividida por uma função:
![]()
Como vimos acima, a regra para a derivada de uma divisão de duas funções diferentes é a seguinte:
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc09ff88e92ee46b5c98d6fc81a5d5a6_l3.png)
Então, calculamos a derivada do numerador e do denominador separadamente:
![]()
![]()
E finalmente, encontramos a derivada da divisão inteira:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\cfrac{10}{x^2+3x-9}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{0\cdot (x^2+3x-9)-10\cdot (2x+3)}{\left(x^2+3x-9\right)^2}=\cfrac{-20x+30}{\left(x^2+3x-9\right)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8f8bdea77dc91b1aff40695511593e86_l3.png)
Na verdade, podemos derivar uma fórmula para diferenciar diretamente quando temos uma constante no numerador dividida por uma função, pois a derivada da constante é sempre 0. Portanto, a seguinte fórmula será sempre verdadeira:
![]()
Exemplo 3
Neste exercício, derivaremos um quociente de dois polinômios:
![]()
Para resolver a derivada, devemos aplicar a regra para a derivada de um quociente de duas funções diferentes, que é a seguinte:
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc09ff88e92ee46b5c98d6fc81a5d5a6_l3.png)
Agora vamos encontrar a derivada do polinômio do numerador e do polinômio do denominador:
![]()
![]()
A derivada da divisão dos polinônimos é, portanto:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\cfrac{x^3+4x^2}{5x^2-8}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-065ad49556f264b4cfb505522ad7566b_l3.png)
E por fim, realizamos as operações e simplificamos ao máximo a fração:
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\\[2ex]&=\cfrac{15x^4-24x^2+40x^3-64x-10x^4-40x^3}{25x^4+64-80x^2}\\[2ex]&=\cfrac{5x^4-24x^2-64x}{25x^4-80x^2+64}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-af3f7cb513883d1fa5dadca23701c19d_l3.png)
Exercícios resolvidos sobre a derivada de um quociente
Derive as seguintes divisões de funções:
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{A) }f'(x)&=\cfrac{(18x+5)\cdot 6x^3-(9x^2+5x)\cdot 18x^2}{\left(6x^3\right)^2}\\[1.5ex]&=\cfrac{108x^4+30x^3-162x^4-90x^3}{36x^6}\\[1.5ex]&=\cfrac{-54x^4-60x^3}{36x^6}\\[1.5ex]&=\cfrac{-9x-10}{6x^3}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-26b0af84dd46ca29727eee97380b4ca4_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{C) }f'(x)&=\cfrac{(24x^2-8x+3)e^{4x}-(8x^3-4x^2+3x)\cdot 4e^{4x}}{\left(e^{4x}\right)^2}\\[1.5ex]&=\cfrac{e^{4x}(24x^2-8x+3-32x^3+16x^2-12x)}{e^{8x}}\\[1.5ex]&=\cfrac{-32x^3+40x^2-20x+3}{e^{4x}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-11f9c8fda61edb1ce51bd33e022a0a24_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{E) }f'(x)&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(\left(4x^2-3x\right)^3\right)^2}\\[1.5ex]&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(4x^2-3x\right)^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ec87daa1a463bacd5a42a1b16e826449_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\text{F) }f'(x)&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{\left(5^{x^2}\right)^2}\\[1.5ex]&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{5^{2x^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bef2b22482e39cea7e82047c0d9911b0_l3.png)
Demonstração da derivada de um quociente
Por fim, demonstraremos a fórmula da derivada de uma divisão. Para fazer isso, usaremos a definição geral de derivada, que é:
![]()
Seja z uma divisão de duas funções diferentes:
![]()
Então, a derivada da função z aplicando a definição matemática será:
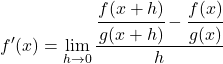
Resolvemos a subtração de frações do numerador da fração:
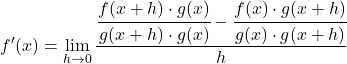
![]()
Adicionar um termo de adição e subtração a uma equação não altera a equação. Podemos, portanto, passar para a próxima etapa:
![]()
Extraímos o fator comum:
![]()
Agora vamos mover o termo h do denominador para o numerador usando as propriedades das frações:
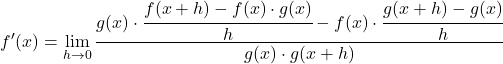
Transformamos a equação aplicando as propriedades dos limites:
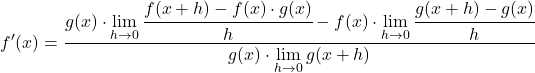
Os limites do numerador correspondem justamente à definição matemática da derivada de cada função, portanto:
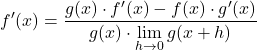
Resolvemos o limite do denominador da fração:
![]()
E assim é demonstrada a fórmula para a derivada de um quociente de duas funções:
![]()