▷ Derivada de um produto (fórmula e exercícios resolvidos)

Neste artigo explicamos como derivar o produto de duas funções (fórmula). Além disso, você poderá ver diversos exemplos de derivadas de produtos de funções e até praticar com exercícios resolvidos sobre derivadas de multiplicação.

Fórmula para a derivada de um produto

A derivada de um produto de duas funções diferentes é igual ao produto da derivada da primeira função pela segunda função indiferenciada mais o produto da primeira função indiferenciada pela derivada da segunda função.

Em outras palavras, se f(x) e g(x) são duas funções diferentes, a fórmula para a derivada da multiplicação entre as duas funções é a seguinte:

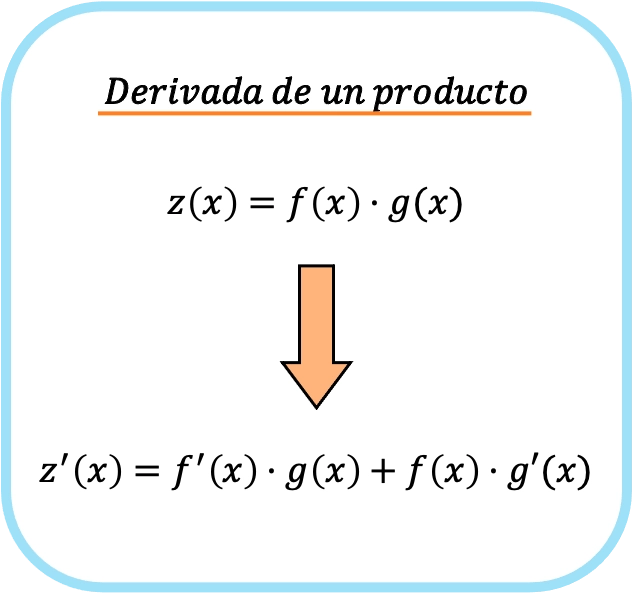
Assim, aplicando a regra da derivada de um produto, passamos de uma simples multiplicação para dois produtos diferentes.

Exemplos de derivada de um produto

Depois de sabermos qual é a fórmula da derivada de um produto (ou multiplicação), resolveremos vários exemplos desse tipo de derivada. Isso tornará muito mais fácil entender como um produto de duas funções é derivado.

Exemplo 1

Neste exemplo resolveremos a derivada de duas funções potenciais multiplicando:

$f(x)=5x^2\cdot (x^3+4x-6)$

Como vimos na seção anterior, a fórmula para a derivada da multiplicação é:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Portanto, devemos primeiro calcular a derivada de cada função separadamente:

$\cfrac{d}{dx}\ 5x^2=10x$

$\cfrac{d}{dx}\ (x^3+4x-6)=3x^2+4$

E uma vez que conhecemos a derivada de cada função, podemos aplicar a fórmula da derivada do produto de duas funções. Ou seja, multiplicamos a derivada do primeiro fator pelo segundo fator sem diferenciar, depois somamos o produto do primeiro fator sem diferenciar pela derivada do segundo fator:

$\begin{array}{c}f(x)=5x^2\cdot (x^3+4x-6)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\end{array}$

Por fim, realizamos as operações para simplificar o resultado obtido:

$\begin{aligned}f'(x)& =10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\\[1.5ex] & = 10x^4+40x^2-60x +15x^4+20x^2 \\[1.5ex] & = 25x^4+60x^2-60x\end{aligned}$

Exemplo 2

Neste caso derivaremos o produto de uma constante por uma função:

$f(x)=7\cdot (x^2+3x)$

A regra da derivada de um produto é a seguinte:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Assim, derivamos separadamente cada função que faz parte do produto:

$\cfrac{d}{dx}\ 7=0$

$\cfrac{d}{dx}\ (x^2+3x)=2x+3$

E então aplicamos a regra para a derivada de uma multiplicação:

$\begin{array}{c}f(x)=7\cdot (x^2+3x)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=0\cdot (x^2+3x)+7\cdot (2x+3)=14x+21\end{array}$

Observe que a derivada de uma constante é sempre zero, portanto podemos deduzir que a derivada da multiplicação de uma constante por uma função é igual ao produto da constante pela derivada da função.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=k\cdot f(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=k\cdot f'(x)\end{array} \end{empheq}$

Exemplo 3

Vamos resolver o produto entre uma função exponencial e um logaritmo natural:

$f(x)=4^{3x}\cdot \ln(x^2)$

A fórmula para a derivada de uma multiplicação de duas funções é:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Devemos, portanto, primeiro fazer separadamente a derivada de cada função que forma o produto, que são as seguintes:

$\cfrac{d}{dx}\ 4^{3x}=4^{3x}\cdot \ln (4) \cdot 3$

$\cfrac{d}{dx}\ \ln(x^2)=\cfrac{2x}{x^2}=\cfrac{2}{x}$

O produto derivado das funções é, portanto:

$\begin{array}{c}f(x)=4^{3x}\cdot \ln(x^2)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=4^{3x}\cdot \ln (4) \cdot 3\cdot \ln(x^2) +4^{3x}\cdot \cfrac{2}{x} \end{array}$

Exercícios resolvidos sobre a derivada de um produto

Deriva os seguintes produtos funcionais:

$\text{A) }f(x)=5\ln(3x)$

$\text{B) }f(x)=(4x^2+1)(6x^3-7)$

$\text{C) }f(x)=\text{cos}(4x)\cdot e^{x^2}$

$\text{D) }f(x)=(3x^3-4x^2+8x)\cdot \sqrt{6x^2+3x}$

$\text{E) }f(x)=5^{4x}\cdot \log_9(x^3-x)$

$\text{F) }f(x)=\left(10x^6-6x^5\right)^4\cdot \text{arcsen}(x^2+9x)$

Veja a solução

$\text{A) } f'(x)=5\cdot \cfrac{3}{3x} =\cfrac{5}{x}$

$\begin{aligned}\text{B) }f'(x)&=8x\cdot (6x^3-7)+(4x^2+1)\cdot 18x^2\\[1.2ex]&=48x^4-56x+72x^4+18x^2\\[1.2ex]&=120x^4+18x^2-56x \end{aligned}$

$\text{C) }f'(x) =-4\text{sen}(4x)\cdot e^{x^2}+\text{cos}(4x)\cdot e^{x^2}\cdot 2x$

$\text{D) }f'(x)=(9x^2-8x+8)\cdot \sqrt{6x^2+3x}+(3x^3-4x^2+8x)\cdot\cfrac{12x+3}{2\sqrt{6x^2+3x}}$

$\text{E) }f'(x)=5^{4x}\cdot \ln(5) \cdot 4 \cdot \log_9(x^3-x)+ 5^{4x}\cdot\cfrac{3x^2-1}{(x^3-x)\ln(9)}$

$\begin{aligned}\text{F) }f'(x)=& 4\left(10x^6-6x^5\right)^3\cdot (60x^5-30x^4)\cdot \text{arcsen}(x^2+9x)\ +\\[1.2ex] &+\left(10x^6-6x^5\right)^4\cdot \cfrac{2x+9}{\sqrt{1-\left(x^2+9x\right)^2}}\end{aligned}$

Derivado de um produto de três funções

A seguir, deixamos vocês com a fórmula da derivada da multiplicação de 3 funções, pois é muito semelhante à de 2 funções e pode ser útil em alguns casos.

A derivada de um produto de três funções é igual ao produto da derivada da primeira função e das outras duas funções, mais o produto da derivada da segunda função e das outras duas funções, mais o produto da derivada da terceira function.function pelas outras duas funções.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=1mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=f(x)\cdot g(x)\cdot h(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)\cdot h(x)+f(x)\cdot g'(x)\cdot h(x)+f(x)\cdot g(x)\cdot h'(x)\end{array} \end{empheq}$

Por exemplo, se quisermos derivar a seguinte multiplicação de três funções diferentes:

$f(x)=3x\cdot e^{2x} \cdot \text{sen}(x)$

Para resolver a derivada devemos aplicar a regra da derivada do produto de três funções, portanto:

$f'(x)=3\cdot e^{2x} \cdot \text{sen}(x)+3x\cdot 2e^{2x} \cdot \text{sen}(x)+3x\cdot e^{2x} \cdot \text{cos}(x)$

Demonstração da fórmula da derivada de um produto

Por fim, demonstraremos a fórmula da derivada de uma multiplicação. Não é preciso memorizar, mas é sempre bom entender de onde vêm as fórmulas. 🙂

Da definição matemática da derivada:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Seja a função z o produto de duas funções diferentes:

$z(x)=f(x)\cdot g(x)$

Então a derivada de z , conforme a definição, será:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{\bigl[f(x+h)\cdot g(x+h)\bigr]-\bigl[f(x)\cdot g(x)\bigr]}{h}$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)-f(x)\cdot g(x)}{h}$

Como sabemos, se somarmos um termo por adição e subtração, isso não afeta o resultado, desde que ambos sejam o mesmo termo. Podemos, portanto, passar para a próxima etapa:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)\color{orange}\bm{-f(x+h)\cdot g(x)+f(x+h)\cdot g(x)}\color{black}-f(x)\cdot g(x)}{h}$

Agora usamos as propriedades do limite para separar o limite anterior em dois limites diferentes:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)-f(x+h)\cdot g(x)}{h}+\lim_{h \to 0}\frac{f(x+h)\cdot g(x)-f(x)\cdot g(x)}{h}$

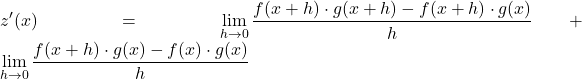
Extraímos o fator comum no numerador das duas frações:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\bigl(g(x+h)-g(x)\bigr)}{h}+\lim_{h \to 0}\frac{g(x)\bigl(f(x+h)-f(x)\bigr)}{h}$

Por outro lado, conhecemos o resultado do seguinte limite:

$\displaystyle \lim_{h \to 0}f(x+h)=f(x)$

Podemos, portanto, simplificar os limites:

$\displaystyle z'(x)=\lim_{h \to 0}f(x+h)\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}+\lim_{h \to 0}g(x)\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

$\displaystyle z'(x)=f(x)\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}+g(x)\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Finalmente, olhando para os dois limites restantes, cada um corresponde à definição da derivada de uma função. A igualdade pode, portanto, ser simplificada:

$\displaystyle z'(x)=f(x)\cdot g'(x)+g(x)\cdot f'(x)$

Ou equivalente:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x) \end{empheq}$

Derivada de um produto (ou multiplicação)

Fórmula para a derivada de um produto

Exemplos de derivada de um produto

Exemplo 1

Exemplo 2

Exemplo 3

Exercícios resolvidos sobre a derivada de um produto

Derivado de um produto de três funções

Demonstração da fórmula da derivada de um produto

Deixe um comentário Cancelar resposta