Derivada da arcotangente

Aqui você encontrará a fórmula da derivada do arco tangente e explicaremos como derivar o arco tangente de uma função com exemplos.

fórmula derivada arcotangente

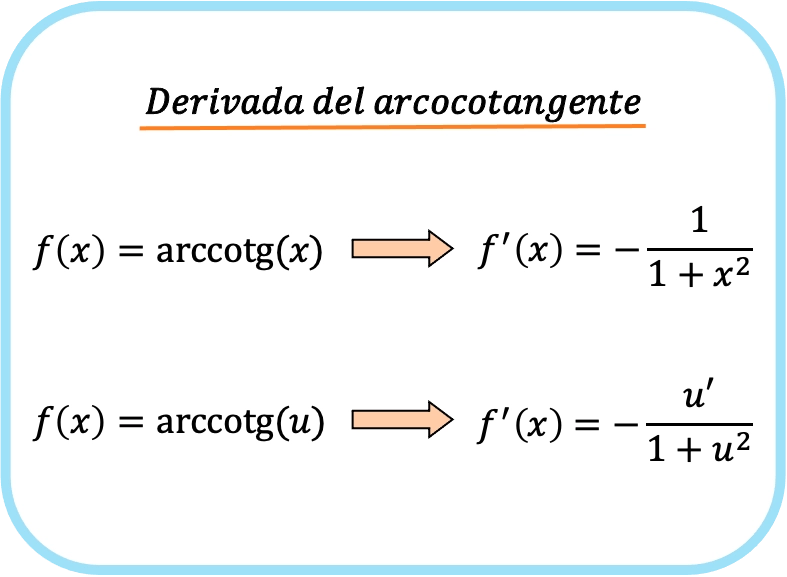
A derivada do arco tangente de x é menos um dividido por um mais x ao quadrado.

$f(x)=\text{arccotg}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{1+x^2}$

Portanto, a derivada do arco tangente de uma função é igual a menos a derivada dessa função dividida por um mais a função quadrada.

$f(x)=\text{arccotg}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{1+u^2}$

Observe que a primeira e a segunda fórmulas são iguais, a única diferença é que a regra da cadeia é aplicada à segunda expressão. Na verdade, se você substituir u por x, obterá a primeira fórmula, pois a derivada da função x é 1.

Embora a arcotangente seja a função inversa da cotangente, suas derivadas são bem diferentes. Na verdade, a cotangente de uma função tem três maneiras de ser derivada, você pode ver todas aqui:

➤ Veja: fórmula da derivada da cotangente

Exemplos de derivada do arco tangente

Depois de ver qual é a fórmula da derivada do arco tangente, aqui estão dois exercícios resolvidos deste tipo de derivada trigonométrica. Lembre-se também que caso tenha alguma dúvida, você pode deixar sua pergunta abaixo nos comentários.

Exemplo 1

Neste exemplo, veremos quanto é a derivada do arco tangente da função quadrática x ² .

$f(x)=\text{arccotg}(x^2)$

No argumento da arcotangente temos uma função diferente de x, então precisamos aplicar a fórmula da derivada da arcotangente com a regra da cadeia:

$f(x)=\text{arccotg}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{1+u^2}$

A derivada de x elevado a dois é 2x, então no numerador devemos colocar 2x e no denominador a função do argumento ao quadrado:

$f(x)=\text{arccotg}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{1+(\left(x^2\right)^2}=-\cfrac{2x}{1+x^4}$

Exemplo 2

Neste segundo exemplo, derivaremos o arco tangente de uma função polinomial de terceiro grau.

$f(x)=\text{arccotg}(x^3-9x+2)$

Usamos a regra da derivada arcotangente para fazer sua derivação:

$f(x)=\text{arccotg}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{1+u^2}$

Portanto, a derivada do arco tangente da função é:

$f(x)=\text{arccotg}(x^3-9x+2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{3x^2-9}{1+(x^3-9x+2)^2}$

fórmula derivada arcotangente

Exemplos de derivada do arco tangente

Exemplo 1

Exemplo 2

Deixe um comentário Cancelar resposta