Derivada da tangente hiperbólica

Aqui você encontrará qual é a derivada da tangente hiperbólica de uma função. Além disso, você poderá ver vários exemplos resolvidos de derivadas de tangentes hiperbólicas. E, finalmente, mostramos a fórmula da derivada da tangente hiperbólica.

Fórmula para a derivada da tangente hiperbólica

A derivada da tangente hiperbólica de x é igual a 1 dividido pelo quadrado do cosseno hiperbólico de x. A derivada da tangente de x também é equivalente ao quadrado da secante hiperbólica de x e 1 menos o quadrado da tangente hiperbólica de x.

$\begin{array}{c}f(x)=\text{tanh}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=\text{sech}^2(x)=1-\text{tanh}^2(x)\end{array}$

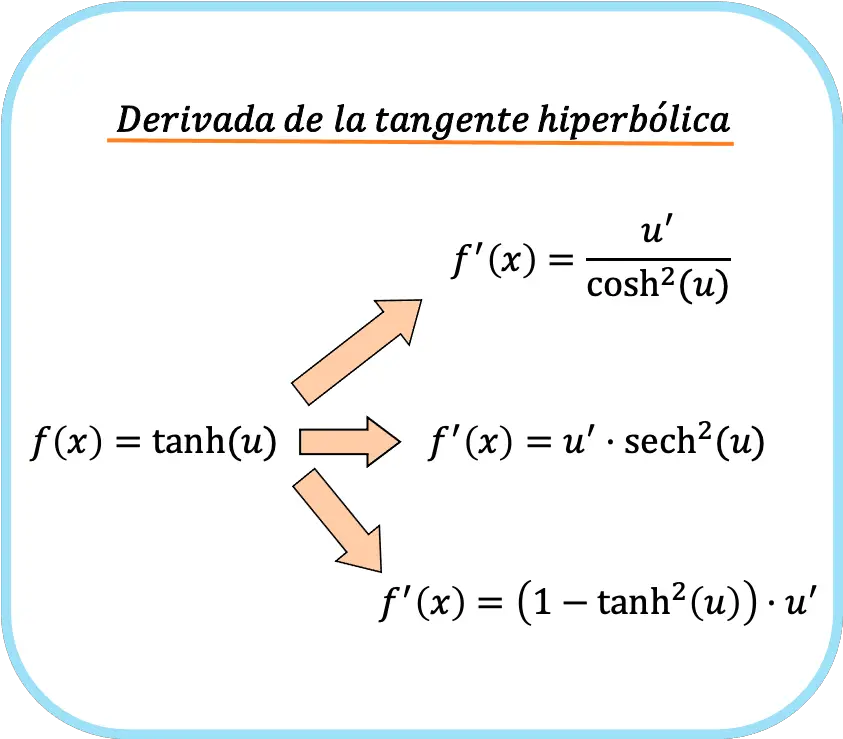
Por outro lado, se no argumento da função tivermos uma função diferente de x, devemos aplicar a regra da cadeia. E então as três fórmulas para a derivada da tangente hiperbólica são:

$\begin{array}{c}f(x)=\text{tanh}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cosh}^2(u)}=\text{sech}^2(u)\cdot u'=\left(1-\text{tanh}^2(u)\right)\cdot u'\end{array}$

Isto não significa que sempre que derivamos a tangente hiperbólica tenhamos de utilizar todas as três fórmulas, mas sim que podemos utilizar qualquer uma delas para derivá-la. Então, dependendo da função do argumento da tangente hiperbólica, será melhor usar uma fórmula ou outra. Abaixo estão vários exemplos nos quais você pode ver como a tangente hiperbólica de uma função é derivada.

A derivada da tangente hiperbólica é quase idêntica à derivada da tangente, mas possui um pequeno detalhe que as torna totalmente diferentes. Você pode ver qual é a diferença no seguinte link:

➤ Veja: fórmula da derivada tangente

Exemplos de derivada da tangente hiperbólica

Depois de ver qual é a fórmula da derivada da tangente hiperbólica, aqui estão vários exemplos resolvidos de derivadas deste tipo de funções trigonométricas para que você entenda perfeitamente como derivar a tangente hiperbólica.

Exemplo 1: Derivada da tangente hiperbólica de 2x

$f(x)=\text{tanh}(2x)$

Para derivar a tangente hiperbólica neste exemplo, usaremos a fórmula do cosseno hiperbólico, embora você possa usar a que preferir.

$f(x)=\text{tanh}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cosh}^2(u)}$

Sabemos que a derivada de 2x é 2, então a derivada de toda a função é:

$f(x)=\text{tanh}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cosh}^2(2x)}$

Exemplo 2: Derivada da tangente hiperbólica de x ao quadrado

$f(x)=\text{tanh}(x^2)$

A regra para a derivada da tangente hiperbólica de uma função é:

$f(x)=\text{tanh}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cosh}^2(u)}$

Por um lado, diferenciamos a função do argumento x ² , que dá 2x, e então resolvemos a derivada de toda a função usando a fórmula:

$f(x)=\text{tanh}(x^2)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cosh}^2(x^2)}$

Exemplo 3: Derivada da tangente hiperbólica ao cubo

$f(x)=\text{tanh}^3(7x^2)$

Neste caso, devemos derivar a tangente hiperbólica de uma função que, além disso, é elevada a uma potência. Portanto, precisamos usar a fórmula da derivada de uma função potencial, a regra da derivada da tangente hiperbólica e a regra da cadeia:

$f'(x)=3\text{tanh}^2(7x^2)\cdot \cfrac{14x}{\text{cosh}^2(7x^2)}}=\cfrac{42x\cdot \text{tanh}^2(7x^2)}{\text{cosh}^2(7x^2)}}$

Prova da derivada da tangente

Nesta seção, demonstraremos a fórmula da derivada da tangente hiperbólica. E, para isso, partiremos da identidade trigonométrica que conecta as três razões trigonométricas hiperbólicas:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

➤ Nota: Para entender a prova, você precisa saber qual é a derivada do seno hiperbólico e qual é a derivada do cosseno hiperbólico . Portanto, recomendamos que você visite as páginas vinculadas antes de continuar.

Agora, vamos aplicar a fórmula da derivada de um quociente:

$\displaystyle\left(\text{tanh}(x)\right)'=\left(\frac{\text{senh}(x)}{\text{cosh}(x)}\right)'$

$\text{tanh}'(x)=\cfrac{\text{cosh}(x)\cdot \text{cosh}(x)-\text{senh}(x)\text{senh}(x) }{\text{cosh}^2(x)}$

$\text{tanh}'(x)=\cfrac{\text{cosh}^2(x)-\text{senh}^2(x)}{\text{cosh}^2(x)}$

Reduzimos a expressão do numerador da fração usando a seguinte fórmula:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

$\text{tanh}'(x)=\cfrac{1}{\text{cosh}^2(x)}$

Como você pode ver, a igualdade anterior corresponde à primeira fórmula da derivada da tangente hiperbólica. Da mesma forma, a secante hiperbólica é o inverso multiplicativo do cosseno hiperbólico, então a segunda fórmula também é derivada:

$\text{tanh}'(x)=\text{sech}^2(x)$