▷ Derivada da tangente (fórmula e exercícios resolvidos)

Aqui você descobrirá como a função tangente é derivada. Além disso, você poderá ver exemplos de derivada da tangente e até praticar com exercícios resolvidos passo a passo. Finalmente, também demonstramos a fórmula da derivada tangente e mostramos a fórmula da derivada tangente inversa.

Qual é a derivada da tangente?

A derivada da tangente de x é igual a 1 sobre o quadrado do cosseno de x. A derivada da tangente de x também é equivalente ao quadrado da secante de x, e 1 mais o quadrado da tangente de x.

$\begin{array}{c}f(x)=\text{tan}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)=1+\text{tan}^2(x)\end{array}$

Todas as expressões são equivalentes, portanto a função tangente possui três fórmulas possíveis para derivá-la.

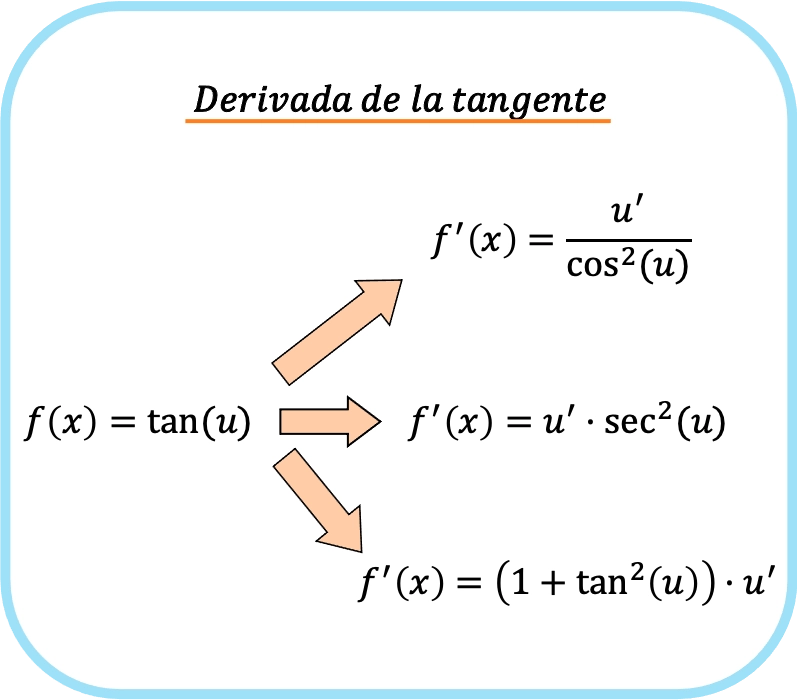
Por outro lado, quando no argumento da tangente temos uma função diferente de x (vamos chamá-la de u), devemos aplicar a regra da cadeia. A derivada da tangente de você é, portanto:

$\begin{array}{c}f(x)=\text{tan}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cos}^2(u)}=\text{sec}^2(u)\cdot u'=\left(1+\text{tan}^2(u)\right)\cdot u'\end{array}$

Resumindo, a regra da derivada tangente pode ser resumida da seguinte forma:

Exemplos de derivada tangente

Dada a fórmula da derivada tangente, nesta seção resolveremos vários exemplos deste tipo de derivadas trigonométricas para que você entenda como derivar a função tangente.

Exemplo 1: Derivada da tangente de 2x

$f(x)=\text{tan}(2x)$

Para calcular a derivada da tangente, você pode usar uma das três fórmulas que vimos acima. Neste caso, usaremos a fórmula do cosseno:

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

A função 2x é linear, então sua derivada é 2. Portanto, a derivada da tangente de 2x é 2 sobre o quadrado do cosseno de 2x:

$f(x)=\text{tan}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cos}^2(2x)}$

Exemplo 2: Derivada da tangente de x ao quadrado

$f(x)=\text{tan}(x^2)$

Neste exemplo, a função de argumento tangente não é um x, mas uma função com derivada. O que significa que precisamos de aplicar a regra da cadeia para derivá-lo.

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

A derivada de x ao quadrado é 2x, então a derivada da tangente de x ² é:

$f(x)=\text{tan}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cos}^2(x^2)}$

Exemplo 3: Derivada da tangente ao cubo

$f(x)=\text{tan}^3(9x^2-4x)$

Neste problema temos uma função composta, portanto também precisaremos utilizar a regra da cadeia para derivar a tangente.

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

Além disso, a tangente é elevada à potência de 3, o que significa que antes de aplicar a fórmula da derivada da tangente deve-se usar a fórmula da derivada de uma potência:

$\begin{aligned}f'(x)&=3\text{tan}^2(9x^2-4x)\cdot \cfrac{18x-4}{\text{cos}^2(9x^2-4x)} \\[2ex]&=\cfrac{3\text{tan}^2(9x^2-4x)\cdot(18x-4)}{\text{cos}^2(9x^2-4x)}\end{aligned}$

Derivada da tangente inversa

Como qualquer função inversa, a função tangente também possui uma inversa, a função arcotangente. Embora a fórmula para derivá-la não seja semelhante à fórmula da tangente, mostramos-lhe porque pode ser útil em alguns casos.

A derivada da tangente inversa de uma função é o quociente da derivada da função dividida por um mais a referida função ao quadrado

$f(x)=\text{tan}^{-1}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

Por exemplo, a derivada da tangente inversa de 3x é:

$f(x)=\text{tan}^{-1}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3}{1+(3x)^2}=\cfrac{3}{1+9x^2}$

Exercícios resolvidos sobre a derivada da tangente

Calcule a derivada das seguintes funções tangentes:

$\text{A) } f(x)=\text{tan}(3x)$

$\text{B) } f(x)=\text{tan}(x^3-10x^2+8)$

$\text{C) } \displaystyle f(x)=\text{tan}^2\left(\frac{x}{2}\right)$

$\text{D) } f(x)=\text{tan}\left(e^{2x}\right)$

$\text{E) } f(x)=\text{tan}\bigl(\ln(4x)\bigr)$

$\text{F) } f(x)=\text{tan}\left(\sqrt{3x}\right)$

Veja a solução

$\text{A) } f'(x)=\cfrac{3}{\text{cos}^2(3x)}$

$\text{B) } f'(x)=\cfrac{3x^2-20x}{\text{cos}^2(x^3-10x^2+8)}$

$\text{C) } \displaystyle f'(x)=2\text{tan}\left(\frac{x}{2}\right)\cdot \frac{1}{\text{cos}^2\left(\frac{x}{2}\right)}\cdot \frac{1}{2}=\frac{\text{tan}\left(\frac{x}{2}\right)}{\text{cos}^2\left(\frac{x}{2}\right)}$

$\text{D) } f'(x)=\cfrac{2e^{2x}}{\text{cos}^2(e^{2x})}$

$\text{E) } f'(x)=\cfrac{\frac{4}{4x}}{\text{cos}^2\bigl(\ln(4x)\bigr)}=\cfrac{1}{x\cdot\text{cos}^2\bigl(\ln(4x)\bigr)}$

$\text{F) } f'(x)=\cfrac{\frac{3}{2\sqrt{3x}}}{\text{cos}^2\left(\sqrt{3x}\right)}=\cfrac{3}{2\sqrt{3x}\cdot \text{cos}^2\left(\sqrt{3x}\right)}$

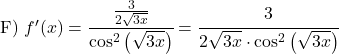
Prova da derivada da tangente

Para que você possa verificar que esta não é uma expressão inventada, nesta seção demonstraremos a fórmula da derivada da tangente utilizando a definição matemática de tangente.

Para fazer isso, partiremos da identidade trigonométrica que conecta as três razões trigonométricas:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

Se usarmos a fórmula da derivada de uma divisão , a derivada seria:

$\displaystyle\left(\text{tan}(x)\right)'=\left(\frac{\text{sen}(x)}{\text{cos}(x)}\right)'$

$\text{tan}'(x)=\cfrac{\text{cos}(x)\cdot \text{cos}(x)+\text{sen}(x)\text{sen}(x) }{\text{cos}^2(x)}$

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}$

Mas, utilizando a identidade trigonométrica fundamental, sabemos que o quadrado do seno mais o quadrado do cosseno é 1:

$\text{sen}^2(x)+\text{cos}^2(x)=1$

$\text{tan}'(x)=\cfrac{1}{\text{cos}^2(x)}$

E assim já chegamos à primeira fórmula para a derivada da tangente. Além disso, a secante é o inverso multiplicativo do cosseno, então a segunda expressão também é derivada:

$\text{tan}'(x)=\text{sec}^2(x)$

Por fim, a terceira regra da derivada tangente pode ser comprovada transformando a fração da etapa anterior em uma soma de frações:

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}$

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)}{\text{cos}^2(x)}+\cfrac{\text{sen}^2(x)}{\text{cos}^2(x)}$

$\text{tan}'(x)=1+\text{tan}^2(x)$

Qual é a derivada da tangente?

Exemplos de derivada tangente

Exemplo 1: Derivada da tangente de 2x

Exemplo 2: Derivada da tangente de x ao quadrado

Exemplo 3: Derivada da tangente ao cubo

Derivada da tangente inversa

Exercícios resolvidos sobre a derivada da tangente

Prova da derivada da tangente

Deixe um comentário Cancelar resposta